机动目标的鲁棒几何法导引律仿真分析

李博文，王 欣

(沈阳理工大学 装备工程学院，辽宁 沈阳 110159)

鲁棒控制是当前控制界的研究热点，以往的系统不可避免的存在各种干扰和未建模动态，这有可能破坏系统的正常工作，这一问题的解决，有待于探索更为有效而鲁棒的制导方法[1-3]。

经典比例导引规律作为最为成熟及应用最为广泛的一种导引律，是在假设导弹和目标速度为常值且目标不机动前提下的最优导引法。但是在实际应用中，为了躲避攻击，敌方机动目标的显著特点就是机动性。目标的机动会严重影响比例导引的性能，导致脱靶量增大。对于我方而言，敌方机动目标的运动规律很难事先知道，只能通过观测手段获取机动目标运动规律。连续运动目标的数学模型是客观存在的，但在实际应用中，由于求取其模型或者过于复杂，或者没有必要，因此，可以把这类目标视之为机动目标。本文基于机动目标，讨论鲁棒几何导引律。并在不同发射角下追击相同目标时，比较比例导引法和鲁棒几何法两种导引律的弹道特性。

1 微分对策制导律

鲁棒几何法是一种建立在现代控制理论基础上的制导律，涉及的基础理论有微分对策制导、李雅普诺夫定理、鲁棒控制理论、微分几何曲线论。

微分对策制导律与比例制导律的不同在于比例制导律要求精确地知道目标加速度，而微分对策制导律不需要知道目标机动加速度的精确信息，只需知道目标的机动能力，即最大加速度。只要目标的加速度小于它的机动能力，无论它采取什么样的机动方式，都能取得保证的性能指标[4-6]，微分对策制导律和比例制导律相比具有强的鲁棒性。

第一类鲁棒性分析问题是在事物所受扰动的形式已知、但扰动范围未知的条件下，分析事物能够维持某种性质所允许的这种形式的扰动范围的大小。在第二类鲁棒性分析问题中，已知事物W及其性质P和事物W的某种形式的扰动及其扰动范围，要给出事物W受到扰动后是否仍具有性质P的确切结论。

2 鲁棒几何制导律仿真原理

鲁棒几何方法仿真的基本原理是根据前两个时间间隔导弹和目标的坐标位置计算出的目标线方位角相对于导弹轨迹弧长的视线角速度、导弹与目标之间的距离相对于导弹轨迹弧长的接近速度、在上一时刻导弹速度方向与目标线方向的夹角、以及目标运动的曲率命令(法向加速度)的大致估计值来确定导弹的曲率命令，导弹的曲率命令同时也是导弹的速度方向在单位距离内旋转的角度，由此可以用迭代法算出导弹在各个时间间隔的坐标位置，并画出导弹的运动轨迹，仿真原理如图1。

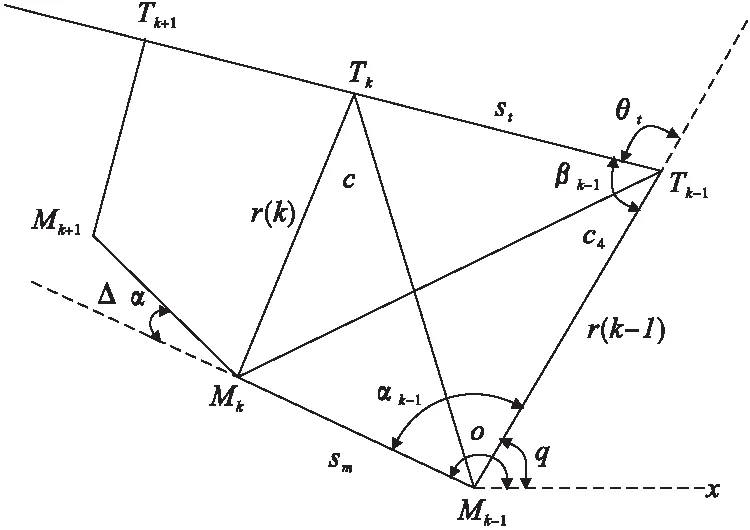
图1 鲁棒几何仿真原理

图中：Tk-1、Tk、Tk+1为目标在第k-1、k、k+1时刻的位置；Mk-1、Mk、Mk+1为导弹在第k-1、k、k+1时刻的位置；q为目标线方位角；o为导弹速度矢量与基准线之间的夹角；αk-1为导弹速度矢量与目标线之间的导弹前置角；βk-1为目标速度矢量与目标线之间的目标前置角；θt为βk-1的补角；Δα为从Mk时刻至Mk+1导弹速度方向的旋转角度；c为Tk与Mk+1之间的长度；c4为Mk与Tk-1之间的长度；st、sm为目标和导弹在一个时间间隔内移动的距离。

算法设计过程中，假设t=0时，导弹位于Mk-1点，目标位于Tk-1点，经过一个时间间隔Δt后，目标运动至Tk点，根据导弹的初始航向角可确定导弹经过第一个时间间隔后的坐标，连接TkMk-1、MkTk-1，那么

c=TkMk-1=

(1)

c4=MkTk-1=

(2)

(3)

θt=π-βk-1

(4)

(5)

Δα=sm·km

(6)

xm(k+1)=xm(k)+sm·cos(Δα)

(7)

ym(k+1)=ym(k)+sm·sin(Δα)

(8)

3 仿真结果分析

仿真参数：导弹的速度为vm=1000m/s，目标速度为vt=400m/s，导弹的初始航向角为45°，目标的初始航向角为45°，导弹的初始坐标为(0，0)，目标的初始坐标：(0，10000)，单位均为m。目标的机动曲率命令为kt=-0.00048375时仿真结果如图2所示。可见，鲁棒几何法在追击作曲线机动飞行的目标时前半程弹道法向过载较大，到后半程时弹道接近直线。这样在前半程时导弹要作较大的机动，因为导弹在弹道后段一般是靠惯性保持飞行状态，火箭发动机只工作很短的时间，所以这种弹道特性能够充分发挥火箭发动机的动力。

图2 目标的机动曲率命令为kt=-0.00048375时导弹追踪轨迹

目标做变轨运动时导弹追踪轨迹如图3所示。由图可知，目标在改变运行轨迹后仍按照原有的速度飞行，导弹弹道前段的弹道曲率有明显的增大，在中间段弹道轨迹平稳、缓和，在导弹-目标距离r<5000m时，导引弹道末端开始弯曲，在接近目标时弹道曲率增大，法向过载的增大导致导弹承受能力受到限制，但是鲁棒几何法下的总体导引弹道比较平缓。鲁棒几何法在目标作变轨运动时，仍能保持较平直的弹道。不需要得到目标精确的曲率命令和速度方位信息，对目标机动具有强的鲁棒性。

图3 目标变轨运动时导弹的追踪轨迹

鲁棒几何法和比例导引法在其它仿真参数不变的情况下，采用不同导弹初始航向角(前置角)的导引弹道进行比较，仿真结果如图4～图7。

图4 导弹初始航向角为90°时鲁棒几何法弹道

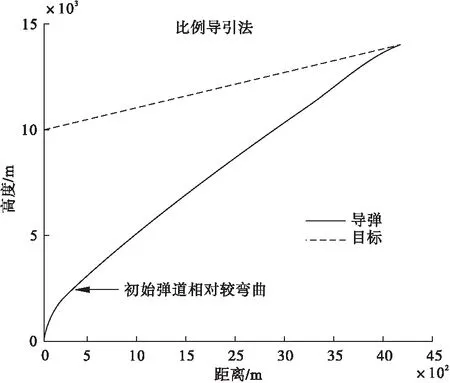
图5 导弹初始航向角为90°时比例导引法弹道

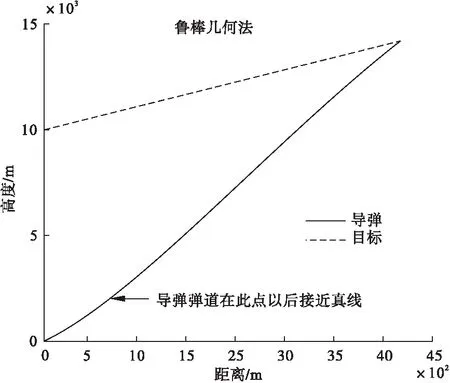
图6 导弹初始航向角为60°时鲁棒几何法弹道

图7 导弹初始航向角为60°时比例导引法弹道

从两种导引律的对比结果来看，鲁棒几何法对初始航向角变化的弹道弯曲程度明显小于传统比例导引律弹道。这说明鲁棒几何法具有较强的鲁棒性，能够抵御一定的外界扰动。经典比例导引律结构简单，易于实现，可以得到较为平直的弹道，但是，命中点导弹需用法向过载受到导弹速度和攻击方向的影响。鲁棒几何法弹道修正的过程只在开始时进行，导弹末端弹道的法向加速度基本为零，末端弹道较为平直。

4 结束语

虽然比例导引法应用广泛，但其在攻击有对抗性的目标时，仍有可能产生很大的脱靶量，所以有必要进一步研究具有更高精度、更实用的导引的目标时，仍有可能产生很大的脱靶量，所以有必要进一步研究具有更高精度、更实用的导引律，以适应发展的需要。而鲁棒几何法正是一种可以满足要求的导引律，鲁棒几何法作为一种现代制导律，它将与目标曲率命令和速度方位信息有关的项视为干扰量，不需要得到目标精确的曲率命令和速度方位信息，弹道需用法向过载分布合理，对抗目标机动和干扰能力强，是一种具有更高精度、更实用的导引律。

[1] 李超勇，齐治国，荆武兴.平面微分几何制导律应用研究[J].哈尔滨工业大学学报，2007，39(7)：1032-1035.

[2] 李忠应.空空导弹全向攻击最优制导规律研究[J].北京航空航天大学学报，1990，16(10)：110 -116.

[3] 胡建和，李忠应.地-空导弹自适应最优制导律初探[J].北京航空航天大学学报，1991，17(3)：101-110.

[4] 张中南，童幼堂，张卫峰.比例导引法导引弹道仿真研究[J].战术导弹技术，2005，(2)：56-59.

[5] 段光仁.线形系统理论[M].哈尔滨：哈尔滨工业大学出版社，1996.

[6] Ben-Asher J Z,Farber N,Levinson S.New Proportional Navigation Law for Ground-to-Air Systems.Journal of Guidence，Control，and Dynanmics[J].2003,26(5)：822-825.