基于粒子群优化的多数据链任务分配模型及方法

田 毅，阎 芳，刘 锐，赵长啸，

(1.中国民航大学 天津市民用航空器适航与维修重点实验室，天津 300300;2.中国民航大学 安全科学与工程学院，天津 300300)

1 引 言

军用数据链始于20世纪50年代，并首先装备于地面防空系统、海军舰艇，而后逐步扩展到飞机。在战术数据链的发展过程中，以美国为首的西方各国在不同的历史时期，根据当时的技术水平和不同的作战需求开发了种类繁多的战术数据链。数据链 已经在近年来的历次局部战争中大显身手：在叙以贝卡谷地的空战中，以色列预警机利用数据链指挥空战以损失1架战机的代价摧毁了叙利亚81架同等性能战机和19个地对空导弹基地；海湾战争中，美国利用数据链使伊拉克80余枚飞毛腿导弹大部分被拦截。因此，数据链技术受到各国的重视。

然而，不同的数据链有不同的特性，想要实现不同数据链的互联互通需要专门的设计[1]。已经有学者着手改善不同的数据链之间的互操作性。Asenstorfer[2]首先讨论了数据链的互操作性问题，通过改进的数据调制解调器(Improved Data Modem)以提高Link-16、Link-22和CDL(Common Data Link )之间的互操作性；Hoekstra[3]指出了在不同的数据链之间实现互联互通的重要性，研究了数据链各层互操作的可能性，提供了一个实现和保持互操作性的概述性方法。提高互操作性的关键因素是支持多种数据链的平台，它们负责转换不同的数据格式并在多数据链间进行任务分发。因此，如何为不同的数据链之间分配不同的任务，且同时满足任务的要求，并遵守数据链的限制是本文的研究目标。

关于任务分配问题，已有很多学者在许多领域进行了研究，如多媒体流应用[4]、社交网络[5]、多智能体系统[6]，一些集中[7]和分布式的[8]的方法被应用到解决任务分配问题。任务分配一个流行的做法是使用谈判或拍卖机制。一个谈判问题是由多个用户试图来达成一个协议或交易，每个用户都希望最大限度地发挥自己的效用，但他们也面临着故障风险。遗传算法作为进化类算法的典型代表，近年来在无人机任务分配问题领域得到了广泛应用[9]，但遗传算法由于其本质上的随机性，求解过程中存在较多劣质搜索过程，导致其在大规模组合优化问题的求解中效率和精度不高。与遗传算法采用群体解的竞争机制来迭代产生最优解不同，粒子群算法采用群体解的合作机制来迭代产生最优解，因此大大提高了收敛速度。此外，粒子群算法概念简单、容易实现，需要调节的参数偏少。本文提出了一种基于粒子群优化(PSO)[10]的算法来解决多数据链间的任务分配问题，最后给出了算例，结果表明本算法可以在满足系统限制的条件下完成任务分配，有效地实现多数据链间的互联互通。

2 问题描述

2.1 任务模型与数据链模型

假设一个平台支持N种不同的数据链L= {l1,l2,…,lN}，我们使用一个数组来描述数据链li(Fi,Bi,Si,Pi)，其中Fi为通信频段，Bi为频谱宽度，Si是数据链的传输速率，Pi是数据链传输信息的消息格式。消息在不同格式之间的转换代价用如下矩阵记录：

为简化描述，将节点要处理的消息定义为其要完成的一个任务。假设节点有M个任务要处理，任务集合={1,2,…,M}。模型化任务为[t,D,p,l]，t是任意连续两个任务间的最小时间间隔，D是任务允许的最大延迟，p为当前的消息格式，l为任务的负载长度。

2.2 问题提出

在优化后的综合集成数据链中，被分配到每条数据链的最多任务数应该被限制以满足各条数据链间的负载平衡。另一方面，最好将任务分配到相同的数据链中，这样会减少在不同数据链间的消息格式的转换代价。因此，在不同数据链间的任务分配要在两个冲突目标间进行权衡。在综合数据链间分配任务即是找到一个带有约束的分配问题：

A:Γ→L

(1)

(2)

目标函数(2)第一部分代表分配到单条数据链任务的最大数目，第二部分代表任务在不同数据链间消息格式转换的代价函数，目标函数即最小化总代价。为平衡目标函数中的两个目标，α、β为各部分的权重值。任务分配中，还需满足其他的一些限制。

(1)带宽限制

分配到一条数据链的所有任务所需的带宽总和不能超过本数据链的最大传输带宽，Size为数据包大小：

(3)

(2)唯一性

不考虑容错即冗余性，所有的任务同一时刻只能被分配到一条数据链，且所有的任务都需要被分配：

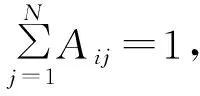
(4)

(3)实时性要求

网络中的任务有实时性要求，即所有的任务都需在规定时限内完成，这进一步要求分配到一条数据链的任务数要被限制，以满足任务完成的实时性要求：

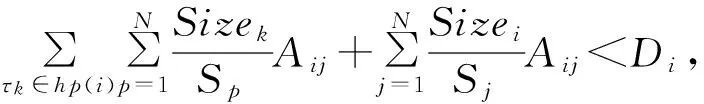
(5)

其中,hp(i)为分配到数据链lj上的所有优先级高于τi的任务集合，Di是任务τi的任务时限。

综上，任务分配问题可以被描述为

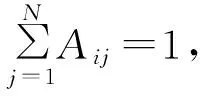
(6)

因此,我们将多数据链间的任务分配问题转化为了求解此优化方程的数学问题。

3 粒子群算法求解任务分配问题

粒子群算法是由Kennedy和Eberhart提出的一种基于population的遗传算法，该算法在对动物集群活动行为观察基础上，利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得最优解。

3.1 粒子群公式

利用粒子群算法的第一步是定义粒子群及求解空间。就求解的任务分配问题，将粒子的求解空间定义为M纬空间，X={xi,x2,…,xM}，其中xi为数据链的索引值，xi∈[1,N]。粒子的位置即任务的分配结果A:→L。粒子的速度向量为V={vi,v2,…,vN}，vi取值范围为在 (-N+1,N-1)的整数，代表距当前位置的最远距离。算法会生成ρ个粒子，随机的初始化各粒子的初始位置和初始速度，算法通过迭代在解空间中寻找最优解。

3.2 适应性函数

适应性函数评价算法中粒子位置的性能，即本文中任务分配结果的性能。目标函数Q(A) 是适应性函数中一项，其他限制条件作为惩罚函数构成适应函数的其他部分。惩罚函数定义为

(7)

则适应性函数定义为

Fit(A)=Q(A)+γPE(A)

(8)

其中,γ为惩罚函数的权重值。适应函数值越小，则此解的性能越好。

3.3 更新粒子位置及速度

在搜寻最优解的过程中，粒子记录两个最优值，Pbest代表粒子在搜寻过程中记录的最优值，Gbest是整个粒子群所经历的最优解。粒子位置和速度的更新公式为

Vt+1=ωVt+c1r1(Pbest-Xt)+c2r2(Gbest-Xt)
Xt+1=Xt+Vt

(9)

式中，ω是粒子保持原来速度的系数，称为惯性权重；c1是粒子跟踪自己历史最优值的权重系数，它表示粒子自身的认识，称为“认知(Cognition)”部分；c2是粒子跟踪群体最优值的权重系数，它表示粒子对整个群体知识的认识，称为“社会(Social)”部分[11]；r1、r2是 [0,1] 区间内均匀分布的随机数。“认知”部分可以由 Thorndike 的效应法则(Law of Effect) 所解释，即一个得到加强的随机行为在将来更有可能出现。这里的行为即“认知”，并假设获得正确的知识是得到加强的，这样的一个模型假定微粒被激励着去减小误差。“社会”部分可以由 Bandura 的替代强化(Vicarious Reinforcement) 所解释。根据该理论的预期，当观察者观察到一个模型在加强某一行为时，将增加它实行该行为的几率，即微粒本身的认知将被其他微粒所模仿。在文献[12] 文中的推荐值为ω=0.9,c1=c2=2。

3.4 算法步骤

粒子群算法步骤如下：

Step 2：设置粒子数及迭代次数；随机初始化各粒子初始位置及速度；

Step 3：计算各粒子的适应性函数;记录各粒子的最佳状态Pbest;记录整个粒子群的最佳状态Gbest,依据公式(9)更新各粒子的速度和位置；

Step 4：检查该状态是否满足式(3)～(5)的限制要求；不能满足，则重复Step 3，直至达到所设置的迭代次数。

首先，输入任务集和数据链的特性；其次，输入粒子算法所需的初始化参数，如粒子的初始位置X和初始速度V；第三，该算法将计算出每个粒子的适应值，并记录最佳解决方案的粒子位置；最后判断所得方案是否满足分配约束。在此算法中，不可行的解决方案在迭代过程中没有被丢弃，它们被用来作为适应函数中的惩罚函数。因此，有必要仔细检查是否满足约束条件，如果解决方案不满足所有的约束，将开始一个新的循环。

4 实验分析

使用仿真方法评估任务分配算法。考虑一个网络，其中有3种类型的数据链，数据链参数如表1所示。在表2中给出了预先定义的任务集合。我们使用消息类型代表该消息的目的平台。参数设置为α=5,β=0.1,γ=300。在粒子群算法中，粒子数和迭代次数分别为20和150。

表1 数据链信息Table 1 The parameters of TDLs

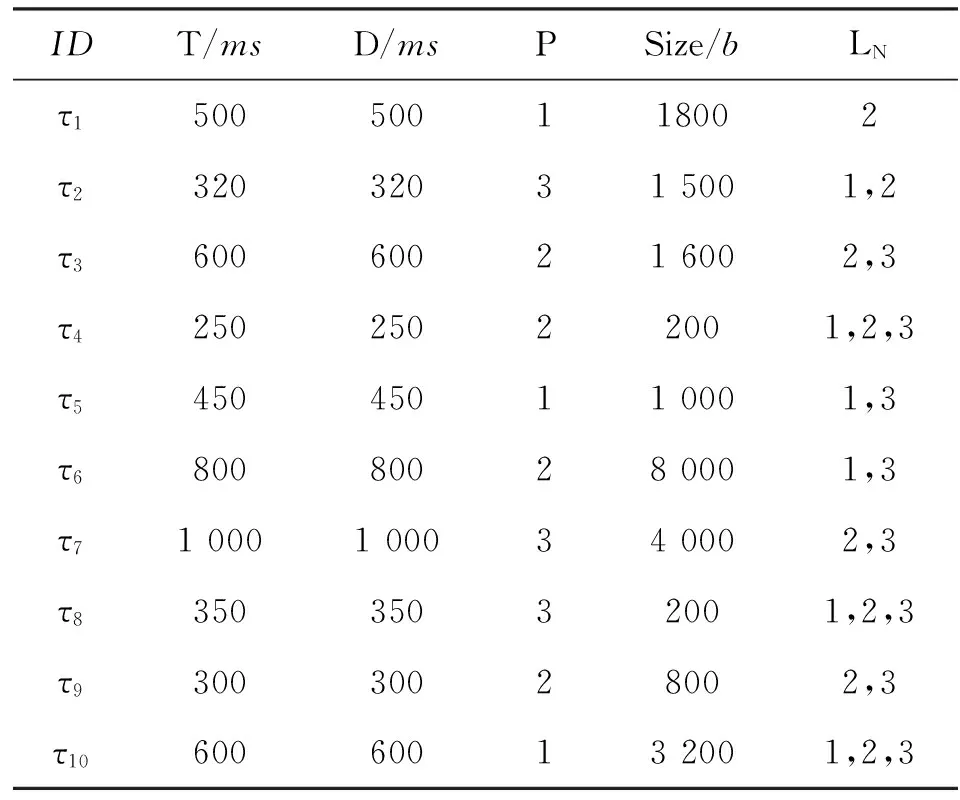
表2 任务信息Table 2 The task set

不同数据链消息模式之间的格式转换的代价被定义如下:定义为转换1 000 b数据所耗的时间代价。例如，将花费0.95 ms将1 000 b的数据从模式1转换到模式2:

迭代结束时，可以得到任务分配的结果,如表3所示。

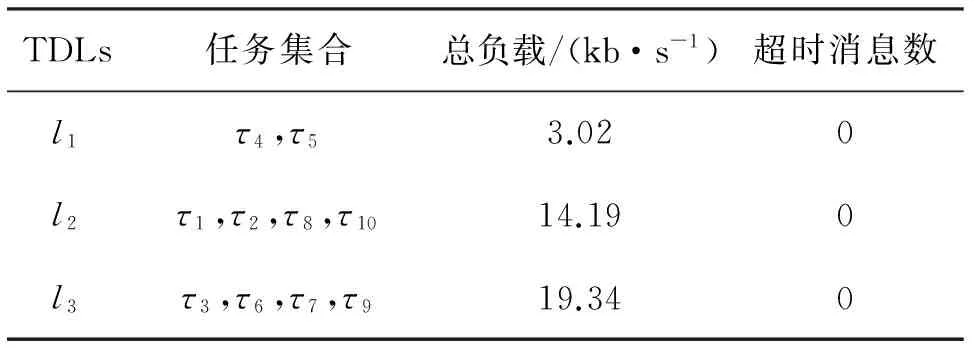
表3 任务分配结果Table 3 Task allocation results

网络中总负载为

和数据链的总容量相比，这是一个中等的流量负荷。因此，如果经过精心设计，所有的任务能够满足其时间期限。实验结果表明，本算法可以在满足所有的约束条件下实现多数据链的任务分配。

5 结 论

不同的数据链有不同的设计，以满足多样化的战术需求，多数据链间的互操作性是发挥协同作战能力的关键。本文模型化数据链和任务，给出了多数据链间任务分配问题的数学模型，并基于粒子群算法对该问题进行了求解。通过模拟计算表明，该算法可满足在不违反任何任务约束条件下实现多数据链间的任务分配，对提高多单位战斗协同效能具有理论指导意义。

下一步的工作包括两个方面：一是寻找求解该问题的最优算法，并比较各算法在执行效率、有效性等方面的优劣；二是求解在给定多数据链性能的条件下，可分配任务数量的上界，在实现多数据链互联互通的同时提高资源利用率。

[1] 焦广伦,孙治水.一种数据链集成架构[J].电讯技术,2013,53(11):1401-1405.

JIAO Guang-lun,SUN Zhi-shui.An Architecture of Data Link Integration [J].Telecommunication Engineering,2013,53(11):1401-1405.(in Chinese)

[2] Tactical Data Link Systems and the Australian Defence Force(ADF)-Technology Developments and Interoperability Issues[R].DSTO-TR-1470,2004.

[3] NATO C3 Agency.Tactical Data Links and Interoperability,The Glue between Systems[R].[S.l.]:NATO C3 Agency,2008.

[4] Paterna F,Acquaviva A,Caprara A,et al.Variability-aware task allocation for energy-efficient quality of service provisioning in embedded streaming multimedia applications[J].IEEE Transactions on Computers,2012,61(7):939-953.

[5] de Weerdt M,Zhang Y,Klos T B.Distributed task allocation in social networks[C]//Proceedings of the 6th International Conference on Autonomous Agents and Multiagent Systems.Honolulu,Hawaii,USA:ACM,2007:17-24.

[6] Ferreira P,dos Santos F,Bazzan A,et al. Robocup rescue as multiagent task allocation among teams:Experiments with task interdependencies[J].Autonomous Agents and Multi-Agent Systems,2010(20):421-443.

[7] Scerri P,Farinelli A,Okamoto S,et al.Allocating tasks in extreme teams[C]//Proceedings of the Fourth International Joint Conference on Autonomous Agents and Multiagent Systems.Utrecht,Holland:ACM,2005:727-734,

[8] Zheng X,Koenig S.Reaction functions for task allocation to cooperative agents [C]//Proceedings of the 7th International Joint conference on Autonomous Agents and Multiagent Systems.Estoril,Portugal:ACM,2008:559-566.

[9] Shima T,asmussen S J,Sparks A G,et al.Multiple task assignmentsfor cooperating uninhabited aerial vehicles using genetic algorithms[J].Computers & Operations Research,2006,33(11):3252-3269.

[10] Kennedy J,Eberhart R.Particle swarm optimization[C]//Proceedings of 1995 IEEE International Conference on Neural Networks.Perth,Australia:IEEE,1995:1942-1948.

[11] Poli R,Kennedy J,Blackwell T.Particle Swarm Optimization:An Overview[J].Swarm Intelligence,2007(1):33-57.

[12] Shi Y,Eberhart R C.Parameter Selection in Particle Swarm Optimization[C]//Proceedings of the 7th International Conference on Evolutionary Programming VII.San Diego,California,USA:Springer-Verlag,1998:1-5.