也谈含参不等式恒成立问题的解法探究

☉江苏省如皋市第二中学 章 丽

也谈含参不等式恒成立问题的解法探究

☉江苏省如皋市第二中学 章 丽

高中阶段我们经常遇到很多恒成立问题，而这种类型的问题是历年来高考中的考查热点，用以考查于学生的灵活性和创造性等思维品质方面的发展水平.教学实践中，教师要能够发挥主导作用，激发学生思维，引导学生细致分析，从多角度、全方位地探究此类问题的解法、思路，从而促进学生综合解题能力的有效提升.下面笔者结合平时教学谈谈对这类问题的一般解法.

一、运用分离变量解决恒成立问题

将变量进行分离，即等式的一边是原不等式的参数，而另一边是原不等式的其余部分，进而求出另一边的取值范围，最终得解.这是解决这类问题的一种最常见的方法，它可以避免分类讨论，减少在操作过程中可能出现的一些错误，使问题得到顺利解决.

例1 已知f（t）=logt，t∈［，8］，对于f（t）值域内

2的所有实数m，不等式x2+mx+4＞2m+4x恒成立，求x的取值范围.

分析：上面不等式中含有两个变量a及x，其中已知x的范围即x∈R，需要求解的就是另一变量a的取值范围，因此可考虑将a与x分离.

点评：当原等式（或不等式）中出现两个变量时，可以引导学生仔细分析、比较，找出两个变量的差异；如果已知其中一个变量的范围，且利用恒等变形易于使两个变量分置在等号（或不等号）两侧，符合以上要求的就可以运用“分离变量”的方法求解.

二、构造函数解决恒成立问题

即将所有变量移到一边，将其变为f（x）≥0或f（x）≤0的形式，再求f（x）的最值或范围.

例3 同例1.

三、利用主、辅元转换解决恒成立问题

这种方法尤其适合参变量次数为一次的恒成立问题，通过将表达式中主、辅元转换，可以达到把复杂紊乱的问题简化为简单直观问题的效果.

例4 若不等式2x-1＞m（x2-3）对满足-1≤m≤1的所有m都成立，求x的范围.

解：我们可以用改变主元的办法，将m视为主变元，即将原不等式化为：m（x2-3）-（2x-1）＜0.

点评：主、辅元互换可以实现对问题的有效转化，由繁到简，应用这种方法的过程中关键还是把握恒成立的本质，巧用转化思想，灵活处理，从而顺利解决问题.

四、运用判别式解决恒成立问题

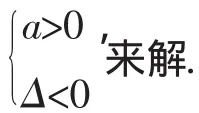
即2x2+（6-2m）x+（3-m）＞0对一切实数x恒成立，所以

Δ=（6-2m）2-8（3-m）＜0，解得1＜m＜3.故实数m的取值范围是（1，3）.

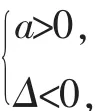
五、运用数形结合解决恒成立问题

把等式或不等式进行合理的变形，运用“数形结合”的思想，将恒成立问题绘制成函数的图像，使得复杂的解题过程得以简化.特别是在解答填空、选择等题型时，通过画图可以形象、直观地得到结果，使我们的解题过程变得十分便捷，大大提高了解决问题的效率.

例6 当x∈（1，2）时，不等式（x-1）2＜logax恒成立，则a的取值范围是______.

分析：此题可以绘成函数图像求解，不等式中不等号两边分别设成两个函数，即左边图像为抛物线，是二次函数；右边图像为常见的对数函数，如此可以迅速得解.

解：设y1=（x-1）2，y2=logax，可绘出y1的图象为如图1所示的抛物线，很容易得出当a＞1，并且必须也只需当x=2时，y2的函数值大于等于y1的函数值，对一切x∈（1，2），y1＜y2恒成立.

故loga2＞1，a＞1，所以1＜a≤2.

点评：运用“数形结合”进行解答时的关键在于将等式（或不等式）进行恰当地变形，然后绘出两边的函数图象，方便快捷，而且不易出错.这种方法非常适合用于那些不需要完整解题过程的题型上.

六、运用函数性质解决恒成立问题

这是一类特殊题型，即定义中隐含了一些恒成立问题.

分析：尽管题中没有明确告知我们这是一个恒成立问题，但依据偶函数成立的条件我们便可以准确地将本题归类为恒成立问题，进而找到解决本题的路径.

解：由题得：f（x）=f（-x）对一切x∈R恒成立，=

点评：从函数的性质出发解决恒成立问题，其基本依据是函数的性质如周期性、奇偶性等.如函数y=f（x）的周期为T，则对一切定义域中的x，f（x）=f（x+T）恒成立；如函数f（x）是奇（偶）函数，则对一切定义域中的x，f（-x）=-f（x）（f（-x）=f（x））恒成立……对于此类题型，我们要能迅速、熟练地找到函数性质与恒成为问题两者之间的联系并依此找到解题的突破口.

七、利用不等式性质解决恒成立问题

利用基本不等式可以很简洁明快地解决某些恒成立问题.

点评：利用基本不等式解决恒成立问题，可以化解分离参数的麻烦，优化解题的过程，但这类问题的关键是要把握恒成立的本质，即寻求充分必要条件，条件找到，问题便迎刃而解.

以上列举都是具有代表性的经典题型，其各种不同的解题策略都是围绕着含参数不等式恒成立问题而展开，其中蕴含了“转化”、“数形结合”以及“迁移类比”等数学思想.在实际运用过程中，我们应当避免机械套用，从题目的具体特征出发来选择恰当的解题策略，解题的熟练与灵活两者并重，切实提高自身分析问题、解决问题的能力和解后反思的良好习惯.

1.阮伟强.不等式恒成立求参数范围问题的再思考［J］.中学数学（上），2013（12）.