一道环球城市数学竞赛题的推广

☉广州大学计算机教育软件研究所 刘凤鸣 朱华伟

一道环球城市数学竞赛题的推广

☉广州大学计算机教育软件研究所 刘凤鸣 朱华伟

1983环球城市数学竞赛秋季赛第一题：

题目 考虑正方形ABCD中的一点M，证明：三角形ABM，BCM，CDM和DAM的中线交点构成一个正方形.

证明：如图1，设E，F，G，H分别是△ABM，△BCM，△CDM和△DAM的重心，P，Q，R，S分别是AB，BC，CD，DA边的中点，显然，四边形PQRS是正方形.

评注：通过观察发现，当点M不在正方形ABCD内时，这个结论仍然成立，证明的方法同上.

下面我们来讨论对于正三角形这一结论是否成立.如果成立的话，重心所构成的正三角形与原三角形是相似的，它们的面积比又等于多少呢？

命题1：已知正三角形ABC和平面上一点M（不与点A，B，C重合），那么三角形ABM，BCM和CAM的重心构成一个正三角形.

证明：如图2，设点O，P，Q分别是三角形ABM，BCM和CAM的重心，点X，Y，Z分别是AB，BC和CA边的中点.

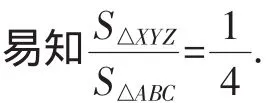
我们不妨对原题进行推广，看看其他正多边形是否也有这种性质，并进一步思考：连接重心得到的正多边形与原正多边形的面积比为多少？

命题2：已知正n边形A1A2…An和平面上一点P（不与点A1，A2，…，An重合）.求证：△PA1A2，△PA2A3，…，△PAnA1的重心也构成一个正n边形.

证明：如图3，设G1，G2，…，Gn为△PA1A2，△PA2A3，…，△PAnA1的重心，点M1，M2，…，Mn为A1A2，A2A3，…，AnA1的中点.

那么正n边形G1G2…Gn与正n边形A1A2…An的面积又有什么联系呢？设正n边形A1A2…An的面积为SA，正n边形G1G2…Gn的面积为SG，正n边形M1M2…Mn的面积为SM.

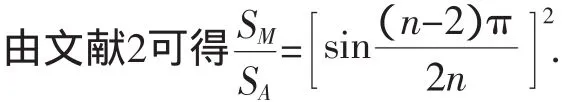
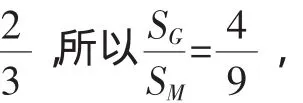
1.中国数学奥林匹克委员会.环球城市数学竞赛问题与解答第1册［M］.北京：开明出版社，2004.

2.包恩萍.正n边形中关于面积的一个数列通项［J］.读写算（教育教学研究），2011（16）.