从一道检测题审视数学试题的命制

☉江南大学附属实验中学 庞彦福

☉江南大学附属实验中学 潘海燕

☉江苏省无锡市南湖中学 葛红兵

从一道检测题审视数学试题的命制

一、问题的提出

☉江南大学附属实验中学 庞彦福

☉江南大学附属实验中学 潘海燕

☉江苏省无锡市南湖中学 葛红兵

八年级期中考试的数学试卷上，一道选择题引来同学们一阵热议和争论.笔者拿来试卷饶有兴趣地看了一下，该题目是：

显然，这是一道用来全面考查学生对全等三角形的几种判定方法掌握情况的一个“不错”的选择题，考查的关键是根据图形和条件，观察、判别角与边的位置关系是否符合判定的条件.对题目的评价，不仅教师有发言权，学生也会有自己不可小觑的看法.

二、学生的困惑

为此笔者找来了一位成绩不错的学生进行询问.

笔者：数学考试的时候，同学们感觉试卷怎么样？

学生：有一道题我觉得好像有问题似的？庞老师，您看就是这道题是不是没有答案呀？浪费了我不少时间！

笔者：你认为呢？

学生：因为公共边AD=AD，当∠ADB=∠ADC，BD= DC时，利用SAS可证明△ABD≌△ACD，所以B正确；当∠B=∠C，∠BAD=∠CAD时，利用AAS可证明△ABD≌△ACD，所以C正确；当BD=DC，AB=AC时，利用SSS可证明△ABD≌△ACD，所以D也正确；因此，排除下来就选择A了.但是，细想想，选项A也能证明△ABD≌△ACD.

笔者：当初为什么选择A呢？

学生：没有SSA这个判断方法，两边和其中一边的对角对应相等的两个三角形不一定全等.

笔者：你为什么又能够说明选项A也能证明△ABD≌△ACD？

学生：连接BC，如图2，由BD＝DC得到∠1＝∠2.

又∠3＝∠4，可以得到∠ABC＝∠ACB，所以就得到AB＝AC.

再利用SSS就可以证明△ABD≌△ACD.

……

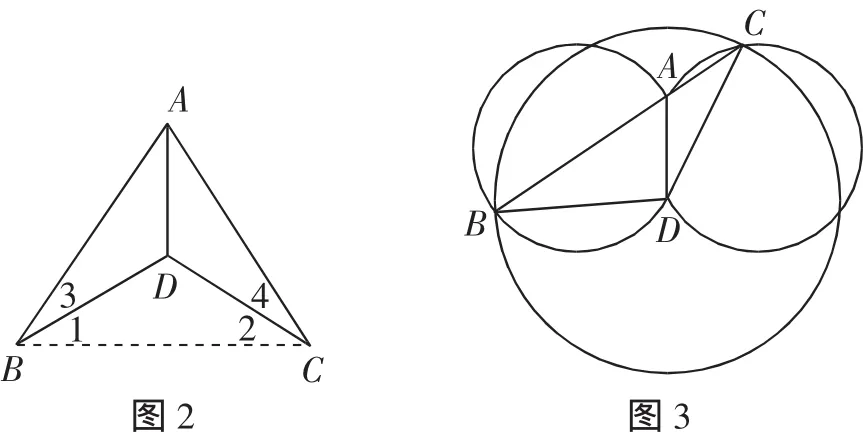
从上述对话可以看出，学生的思考、认识和理解都是很清晰的，推理过程也是完全正确的.为了谨慎起见，笔者用几何画板进行验证，当得到如图3的情形时，显然△ABD与△ACD不全等，但是这已经偏离了试题本身考查的本意.由这个图形可以看出，从某种角度来考虑满足选项A（即∠B＝∠C，BD＝DC）的条件可能会得出两个图形不全等，但并不能说明此题没有问题.该题提供的是图2的情形，通过添加辅助性，进行二次全等的证明确实能证明△ABD与△ACD全等.

笔者在网上搜索一下，找到了这道题目的“原型”，是2011年南昌市中考试卷的第10题，与期中考试的题目不同的是原题多了两个字“直接”，原题是“不能直接证明△ABD≌△ACD的是”.仅两字之差，意义已经不同，漏洞随之产生，这充分体现了数学的严谨性.

三、试题命制的原则

《课标（2011年版）》在“评价建议”部分指出：“评价的主要目的是全面了解学生数学学习的过程和结果，激励学生学习和改进教师教学.评价应以课程目标和课程内容为依据，体现数学课程的基本理念，全面评价学生在知识技能、数学思考、问题解决和情感态度等方面的表现.”考试是最常见的一种评价方式.数学试题的命制应遵循一些基本的原则，体现数学学科的特点和思想.关于数学题目，章建跃博士认为：“真正的数学题应该满足一些基本条件，例如：反映数学本质，与重要的数学概念和性质相关，不纠缠于细枝末节，体现基础知识的联系性，解题方法自然、多样，具有发展性，表述形式简洁、流畅且好懂等.”

1.科学性

数学是严谨的科学，题目的编制与呈现应当遵循数学的原理和规律，准确把握试题的基础性与科学性，不违背常理，体现数学的真正价值.命题应体现课标理念，科学性和严谨性是最基本的要求.根据考试的层次不同（如月考（有的学校或地方还有“周考”）、期中联考、县（区）级统考或调研测试、学期末测试、学年末测试、模拟、中考等），试题命制的要求和规格也会不同.阶段性测试往往更重视基础性、针对性、易错点等.

譬如学习过等腰三角形之后，笔者设计了这样一个题目：已知等腰三角形一腰上的高与另一腰的夹角为40°，那么这个等腰三角形的顶角度数为________.

设计这个题目不仅是为了考查学生对分类讨论思想的理解，而且还要考虑到学生对等腰三角形的概念的理解及掌握情况.如果同学们对三角形的分类不能信手拈来的话，就未必能考虑到锐角等腰三角形和钝角等腰三角形两种情况（直角等腰三角形显然不符合题意），从而出现漏解的现象，同时也能进一步固化钝角三角形的高.数学学习打好基础是很重要的，基础是进一步学习和发展的基石，数学学习需要理解，需要学会思维的方法.

2.适宜性

学生是有差异的，学校不同、班级不同，命制试题的难易程度当然是有区别的.对于基础好的学生做的试卷，如果拿来给基础薄弱的学生当作考试卷，能不难吗？基础不一样，接受的能力当然是有区别的，如果还用同一标准进行衡量、评价当然是不适宜的.《课标（2011年版）》明确指出：“评价结果的呈现和利用应有利于增强学生学习数学的自信心，提高学生学习数学的兴趣，使学生养成良好的学习习惯，促进学生的发展.评价结果的呈现，应该更多地关注学生的进步，关注学生已经掌握了什么，获得了哪些提高，具备了什么能力，还有什么潜能，在哪些方面还存在不足.”因此，阶段性的测试考试试卷的命制与设计要充分考虑学生的实际情况，命制出合理的、适宜的、有针对性的试卷，才能有利于发现教师教学中存在的问题，有助于发现学生学习过程中的遗漏或制约因素，更好地为教师的教学及学生的学习提供改进的措施.

3.规范性

试题由题设到提问，作为一个整体，必须严谨无漏洞，不产生歧义，不存在逻辑上的错误，不会引起考生不必要的猜测和误解，才能保证考试的正常发挥，否则会降低考试的功能和效度.数学试题的命制必须符合数学的规范要求.

4.导向性

考试试题的命制要有明确的指向性.考试是为了检查过去的教与学，更是为了指向今后的教与学.

请看2012年丽水市中考数学试题填空题中的压轴题：

如图4，在梯形ABCD中，∠A=90°，∠B=120°，AD=，AB=6.在底边AB上取点E，在射线DC上取点F，使得∠DEF=120°.

（1）当点E是AB的中点时，DF=________；

（2）若射线EF经过点C，则AE=________.

第（1）问比较容易得出.

解得x=2或5.故答案为2或5.

四、试题命制的方法

考试试卷上的题目来源是有多种渠道的，遴选和改编试题是命制试题的核心性工作.考题可以是教科书上的原题，可以是教材（包括教辅用书）内容、各地测试题、中考题的改编题，可以是命制者的原创题.无论是哪类题都要认真考虑，仔细推敲，避免出现科学性错误或与实际不相符合的表述.

1.制定双向细目表

凡事预则立，无预则废，试题命制也应如此.首先要从思想上认识到命制试卷的重要性，要明白“命题”和“组卷”的区别，命制试卷体现的是责任心，是业务水平.命制试卷时，应该先制定双向细目表，依据课标、教材等教学内容与拟考试的内容有效地进行融合，将要考查的内容、知识点以最恰当的方式呈现出来.选题不能“眉毛胡子一把抓”，一份试卷题量有限，基本题，中等题，较难题比例要适宜，既要涵盖学生应该掌握的主要知识点，又要把重要的核心知识点充分体现出来，把学生容易弄错的地方暴露出来，把引领教学导向的思想方法彰显出来.

2.精选原题

教科书选择的题目基本上是教育教学专家及课程专家经过深思熟虑而选定的，具有一定的代表性、典型性和普适性，各种类型的考试都可以选择一定量的教材中的原题作为考试试卷中的题目.譬如：

设AB、CD是⊙O的两条弦，AB∥CD，若⊙O的半径为5，AB=8，CD=6，则AB与CD之间的距离为_____________.

这是“圆”一章中的一个经典题目了，不同版本的教科书都曾出现过类似的“影子”，或是填空，或是选择，或是解答.命制试卷选用这样的经典题目对教学也是一种导向，意在引导我们的教学要重视课本，立足课堂，注重基础.当然，作为选择题或填空题时，要变化一下教科书中的数据，以免有的学生刚刚做过且记住了答案，就不思考了.

3.改编试题

改编试题的方法有很多，同样一道题目经不同的老师改编后的结果也会各种各样.但无论怎么变化，评价试题质量优劣的标准是该题的科学性、合理性以及有效性，其质量和水平是教师专业能力的体现.将已有的一些现成的好题经过适当改编形成新的试题，改编题可以来源于陈题、旧题，可以是课本上的例题、习题、资料典型题、热点问题为主，力求“问题在书外，而根在书本”，让人感到能在课本中找到问题的“影子”，也可选一些学生常常出现错误的题目.

下面是利用黄金分割改编的问题.

如图5，已知AB=1，点C是线段AB的黄金分割点（AC＞BC）.

（1）试用一元二次方程的求根公式求出黄金比.

（2）如图6，取线段AC的黄金分割点C1（AC1＞CC1），计算BC1的长度，并据此判别点C1是否为线段AB的另一黄金分割点.

4.原创试题

好的原创题往往是一份试卷的亮点，原创题的立意更为重要，一个立意好的原创试题，既能正确地诊断出学生在学习过程中存在的知识漏洞和认知方法上的欠缺，还能为学生参加大型考试积累过程性经验，更能有效地引领学生的学习和思考.原创题要以学生已有知识经验为基础，立意新颖，着重考查学生发现和提出问题的能力、分析和解决问题的能力.

命制试题与课堂教学一样，是一门艺术，而且是一门遗憾的艺术.对于平时的阶段性考试或者是区域性的学业水平测试来说，有机会参与命题的老师，应该珍惜机会，做到细心思考、苦心经营、精心设计.在命制试题时，切实把握好数学的科学性、严谨性和实用性.因为一份考试卷既是考查学生的学情反馈，更是发展教师引领教学的风向标.

1.符永平，刘东升.命题应该追问“数学”［J］.中学数学（下），2013（7）.

2.章建跃.发展数学的内在力量，为学生谋取长期利益［J］.数学通报，2013（2）.

3.钟珍玖，庞彦福.初三数学总复习策略再探——谈二轮复习的选题原则、方法和评价［J］.中学数学（下），2013（11）.

4.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

5.庞彦福，钟珍玖，武益燕.从解题策略审视运算错误［J］.中学数学（下），2013（8）.

6.庞彦福.教师写作的素材从哪里来［J］.中学数学数学参考（中），2012（10）.FH

·江苏省南通市符永平名师工作室·