对一道高考试题的推广*

☉甘肃省兰州市第二十七中学 陈鸿斌 高素环 安 熙

对一道高考试题的推广*

☉甘肃省兰州市第二十七中学 陈鸿斌 高素环 安 熙

（1）求M的方程；

（2）C，D为M上两点，若四边形ACBD的对角线CD⊥AB，求四边形ACBD面积的最大值.

本题是2013年新课程高考数学理科试题全国卷Ⅱ第20题.本题虽然考察常规，但是平凡中出新意，内涵丰富，很有开发的价值，无疑是一道经典之作.本题的原型可追溯到2009年普通高等学校招生统一考试全国Ⅱ卷理科数学第16题.

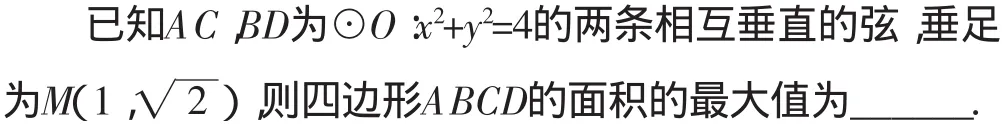
文［1］、［2］分别对此问题作了研究，并且给出了圆中以垂直弦为对角线的四边形面积最值问题的一些一般性结论.

笔者在文［3］中曾讨论了圆锥曲线中以同过焦点或中心的垂直弦为对角线四边形的面积最值问题.文［3］中探究的问题与本题有相似之处，不同点在于本题讨论一条对角线过焦点，另一条无限制，求面积的最值问题.

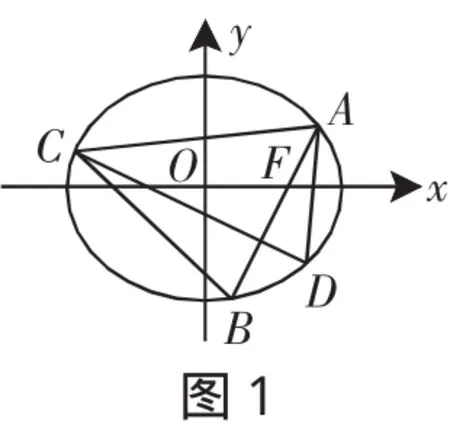
证明：不妨设F为椭圆M的右焦点（c，0），弦AB的倾斜角为θ∈［0，π）.如图1所示.

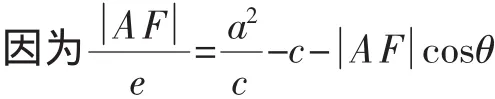
当且仅当t=0，即直线CD过椭圆M的中心时，取“=”号.

当直线CD的斜率不存在时，弦AB为长轴，当且仅当弦CD为短轴，过M的中心时，四边形的面积最大，即Smax=2ab.在式①中，令θ=0，则S≤2ab.所以当直线CD的斜率不存在时，仍然满足式①.

综上可知，当直线CD过M的中心时，四边形ACBD的面积取得最大值

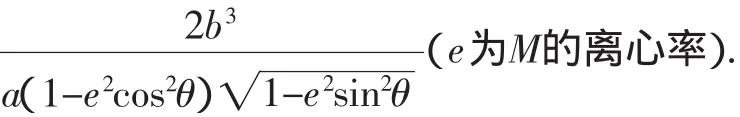
在左焦点（-c，0）处结果与上相同.

把上述结论加强，如果直线CD过M的中心，且四边形ACBD的对角线CD⊥AB，那么四边形ACBD面积的最大值又会是多少呢？

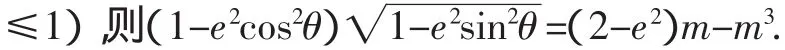
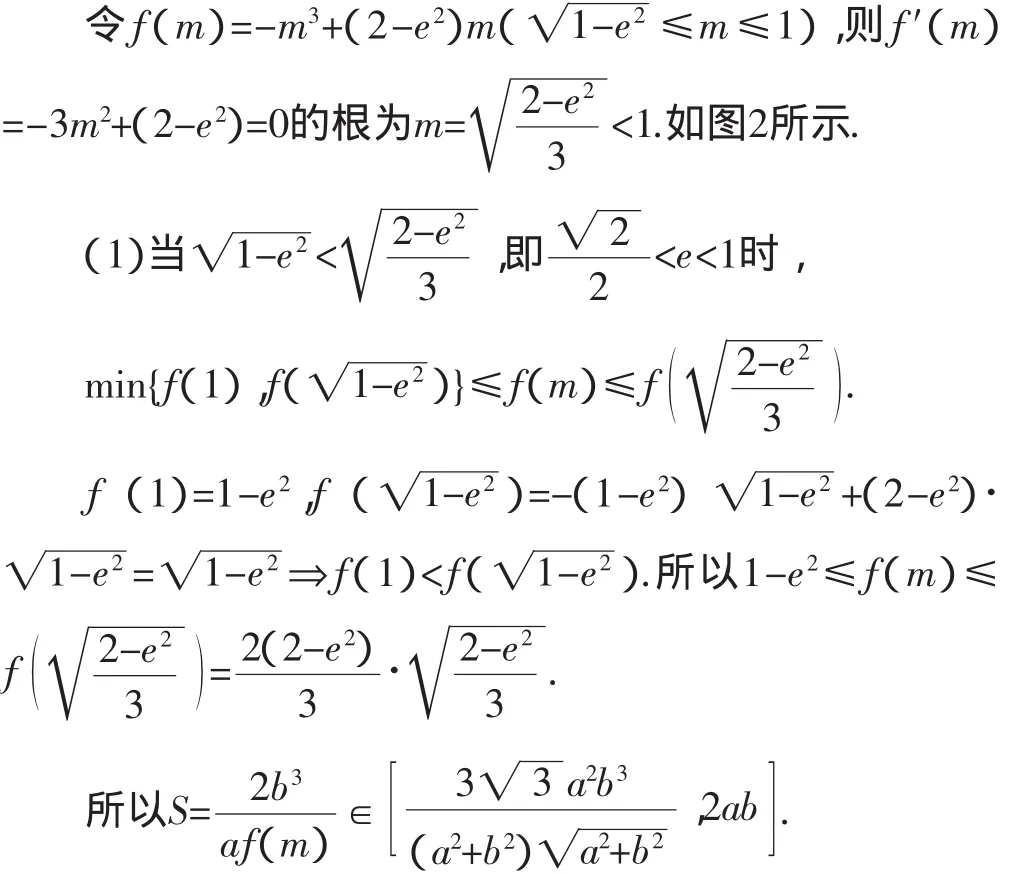
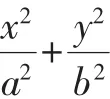
1.侯典峰.一道高考题的几个思维层次［J］.中学数学（上），2009（8）.

2.黄萍.对一道高考填空题的再拓展［J］.中学数学（上），2009（11）.

3.陈鸿斌.一道经典高考题的再研究［J］.中学数学研究（江西），2011（4）.

*本文是甘肃省教育科学“十二五”规划课题“新课程背景下高考数学与学生创新意识培养的策略研究”（课题批准号：G S［2 0 1 3］G H B 0 4 6 8）的阶段性成果.