由一道三角形面积题引发的研究性学习

☉安徽省马鞍山市二中实验学校 陈婷婷

☉安徽省马鞍山市外国语学校杭仁礼

由一道三角形面积题引发的研究性学习

☉安徽省马鞍山市二中实验学校 陈婷婷

☉安徽省马鞍山市外国语学校杭仁礼

新课程改革的核心是课程改革，而课程实施的基本途径是课堂教学.那种片面强调知识传授的“填鸭式”教学既背离了培养创新人才的大方向，也低估了学生自身所蕴藏的学习的创新意识和积极性.其实，每一位学生自身都蕴藏着创新的潜能，这需要我们的培养和发掘，要发掘学生的创新思维和能力，就要整合教师、学生、内容和环境之间的关系.而研究性学习注意的是教师、学生、内容和环境四个方面的优化与整合.这样的教学才是充满活力的、生长性的、个性张扬的、和谐的课堂，才能真正把学生蕴藏的创新思维与创新能力发掘出来.学生也欢迎这样的教学改革，因为他们从中可以学到分析和探究问题的能力，也得到研究和发现的乐趣.

一、例题呈现及解答

例题 已知△ABC的三边长a=5，b=12，C=13，求△ABC的面积.

解：因为a=5，b=12，c=13，

不难发现52+122=132，

所以三边满足a2+b2=c2的关系，

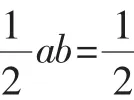
本题的设计意图是想让学生用勾股定理先判断△ABC为直角三角形，再用三角形面积公式求解，同学们很快完成了任务.到这里，本应该结束，进入到下一题，但是随着学生的一声提问，使得问题的深度不断加深.

学生1：如果△ABC的三边不满足勾股定理，构不成直角三角形，对于任意△ABC，能否用其三边a，b，c来表示其面积呢？

二、对问题的一般性研究

1.引领归纳，探究新知

在对原来的问题进行研究之后，随即对学生1进行了表扬，此时这位同学热情十足，大家也纷纷思考起来.

在学生1总结归纳完之后，课堂上同学们议论着、探求着、思索着，有时听到学生的欢呼——数学如此美丽！公式如此优美！

2.迁移类比，真假难辨

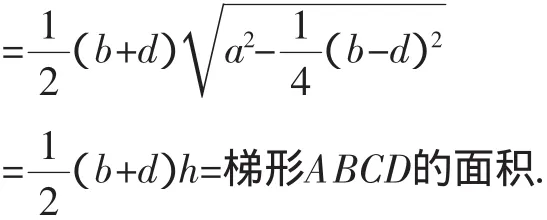
这次的验证结果又一次支持了我们的猜想.但是，如果换成一般的梯形，结论又不成立了.这些对对错错的结果给我们虚虚实实的感觉，无法辨别真假，究竟我们从中能得到哪些启示呢？由我们验证的结果看，我们的猜想一定不是一般四边形的面积公式，而是某一类四边形的面积公式，考查我们验证正确的矩形和等腰梯形，你能发现它们有什么共性吗？

学生5：它们都是轴对称图形.

学生6：它们的各边中垂线都相交于一点.

学生7：它们都是圆的内接四边形.

三、归纳总结，课后反思

经过同学们课上和课下的讨论和思考，得出如下结论，现整理如下：

这堂课本身是一堂预设与生成不一致的研究型学习案例，作为一名一线教师，应大胆鼓励学生的这种探究精神，保护动态的课堂生成过程，为学生创设一个和谐的、可持续发展的、生机勃勃的课堂氛围，为他们的思维活动留下发展的空间.这样的教学也使得学生在相互探索、交流、小组活动中，彼此切磋解题技能，锻炼思维能力，使学生在鼓励中创新，在鼓励中求变，从而实现互利双赢的教学目标.FH