由一道抽奖问题总览概率全貌

☉江苏省海安县立发中学 丁佐宏

由一道抽奖问题总览概率全貌

☉江苏省海安县立发中学 丁佐宏

从近几年高考命题来看，概率创新题层出不穷.例如2013年北京理空气质量问题；2013年江西理以平面几何为载体，2013年陕西理投票问题…….从位置来看都是解答题前三道大题中的第2或第3道，可见命题人至多是将其列为中等题型.但由于背景创新层出不穷，使考生有应接不暇之感.备考中只要我们相应的概率模型，将其本质进行透彻研究，即可以不变应万变，下面以一道抽奖问题为例总览概率问题全貌.

题目：某商场因店庆临近特举行抽奖活动，店庆日在店内消费的顾客均可凭消费票据参加抽奖.抽奖箱内共有四种小球，分别标有“生”“意”“兴”“隆”四个字，顾客每抽奖一次，操作流程为任意取出一个小球并记录小球上的汉字，然后将小球放回抽奖箱继续取出小球记录汉字，重复上述操作至多四次；如取出的小球上标有“隆”字，则抽奖环节结束，不再重复取球至四次.奖励的规则为：一等奖获得者需取到“生”“意”“兴”“隆”四个字的小球，且取球顺序与词组顺序固定相同；二等奖获得者需取到“生”“意”“兴”“隆”四个字的小球，取球顺序不限；三等奖获得者需取到“生”“意”“兴”三个字的小球.

（1）求某人抽奖一次获得二等奖的概率；

（2）甲、乙两人参与抽奖，则两人均获得一等奖的概率；

（3）求某人抽奖一次，中奖的概率；

（4）求某人抽奖三次，恰有二次中奖的概率；

（5）设摸球次数为ξ，求ξ的分布列和数学期望.

一、中奖概率的求解看计数原理及排列组合的运用

解：（1）设“摸到二等奖”为事件A.

点评：此问为有序问题，故在计算相应事件数时应采用排列方式.

二、由同时中奖看独立事件同时发生

解∶（2）设“某人摸到一等奖”为事件B，则

点评：甲、乙两人均中一等奖相互独立，独立事件同时发生用乘法计算.

三、由中奖结果的互斥看概率的加法

解∶（3）某人抽奖一次，中奖的结果可能为一等奖、二等奖、三等奖，且中一等奖、二等奖或三等奖为互斥事件，互斥事件至少有一个发生的概率用加法求解.

设获得三等奖为事件C，其包含的情况有：“生，意，兴”三个球外加“生”、“意”、“兴”三种情况.

故某人抽奖一次，中奖的结果可能为一等奖、二等奖或三等奖的概率为：

点评：如果事件A与事件B不能同时发生，那么事件A或B发生的概率为二者之和P（A+B）=P（A）+P（B）；同理，如事件A，B，C，…，X互斥，那么这些事件发生的概率同样为各事件发生概率之和，P（A+B+C+…+X）=P（A）+P（B）+ P（C）+…+P（X）.

题目变式：某商场举行优惠促销活动，规则为每位顾客消费满100元可转动转盘一次（如图所示），转盘指针停留区域的数字为返券金额.指针可能停在转盘的任何位置，停在A、B、C三个区域返券金额分别为60元、30元、0元.顾客转动转盘的次数为实际消费金额/100的整数倍，累计返券金额为每次转盘返券金额之和.某顾客消费220元，他参与转盘活动获得的返券金额为X（元），求其分布列与数学期望.

由题意得，该顾客可转动转盘2次.随机变量X的可能值为0，30，60，90，120.

所以，随机变量X的分布列为：

30 60 90 120 1 P0 X1 43 5 1 8 1 9 1 3 6

四、由中奖次数看事件的对立

点评：在一次抽奖过程中，中奖与不中奖不可能同时发生，所以这两个事件也是互斥事件.但中奖和不中奖必然会发生其中一种情况，可将其视为对立事件，即二者发生其一的概率为100%，如事件A的对立事件为，那么P（A）+P）=1.

由此可以看出，互斥事件未必为对立事件，但对立事件必为互斥事件，可将互斥作为对立事件的必要不充分条件，对立作为互斥事件的充分不必要条件.

五、由摸球次数引出离散型随机变量概率分布

故取球次数ξ的分布列为：

ξ1234 P1 4 3 1 6 9 6 4 27 64

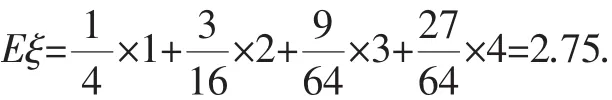
点评：将随机变量的取值及其概率用分布列形式写出后，还需要进行检验来确保分布列正确，检验公式为：（1）pi≥0（i=1，2，…）；（2）p1+p2+p3+…+pn=1.数学期望：E（ξ）=x1p1+x2p2+…+xnpn.ξ的数学期望是ξ各种取值的平均数，如ξ的不同值概率相等就是简单平均数，若ξ的不同值概率不全相等就是加权平均数.

综上所述，所谓概率学，就是对事物发生的可能性进行研究的一门科学，我们在生活和工作学习中必然会遇见各种各样的“事件”，这些事件的发生有一定的规律可供我们掌握，通过学习概率学知识，有助于我们尽可能的避免有害事件的发生，提高有益事件的发生概率，从而提高妥善应对不同事件的能力.在学习过程中，命题形式各有不同、千变万化，但问题本质相同，正所谓万变不离其宗，我们在解题训练过程中一定要注意基础知识的扎实掌握和解题技巧的灵活运用，便可以有效的提高实际解题能力.除文中所述的解题思路和技巧外，我们还可以运用分类讨论等数学思想，不断拓宽解题思路，从而不断提高数学知识的运用能力.

1.陈忠怀.骰子赌博揭开概率统计之谜［J］.中学数学（上），2011（8）.

2.悦瑞娟.离散型随机变量分布列问题的寻解历程［J］.高中数理化，2013（7）.

3.徐君华.创设概率背景 凸显命题立意［J］.中学数学（上），2013（8）.