走进拓展，竟如此美丽——记2013年江西中考几何压轴题的研究与拓展

☉江西省安福县城关中学 曹经富

☉江 西 省 教 研 室 陈莉红

走进拓展，竟如此美丽
——记2013年江西中考几何压轴题的研究与拓展

☉江西省安福县城关中学 曹经富

☉江 西 省 教 研 室 陈莉红

中考压轴题或课题学习类试题，通常以学生熟悉、感兴趣、有价值的素材或数学活动为切入点，立足于知识、问题的生长点、发展点、延伸点，借助操作活动、经验、知识、思想方法等，培养感性直觉和理性思考为目标，重在考查考生发现问题、提出问题、分析问题和解决问题的能力.作为数学教师，在日常教学中，如果挑选一些具有广阔前景的中考试题，进行适当的拓展与延伸，深入思考与探究，举一反三，放弃题海战术，以一当十，我们就能获得最大限度的收获.现以2013年江西中考几何压轴题为例进行拓展与延伸，与大家分享与探讨.

例：（2013年江西）某数学活动小组在作三角形的拓展图形，研究其性质时，经历了如下过程.

●操作发现：

在等腰△ABC中，AB=AC，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图1所示，其中DF⊥AB于点F，EG⊥AC于点G，M是BC的中点，连接MD和ME，则下列结论正确的是_________.（填序号即可）

●数学思考：

在任意△ABC中，分别以AB和AC为斜边，向△ABC的外侧作等腰直角三角形，如图2所示，M是BC的中点，连接MD和ME，则MD和ME具有怎样的数量和位置关系？请给出证明过程.

●类比探索：

在任意△ABC中，仍分别以AB和AC为斜边，向△ABC的内侧作等腰直角三角形，如图3所示，M是BC的中点，连接MD和ME，试判断△MED的形状.

答：__________________.

解析：操作发现：①②③④.

数学思考：MD=ME，MD⊥ME.

类比探究：等腰直角三角形.

评析：本题以动态三角形为背景，以两边为斜边向外构建等腰直角三角形，探究两直角顶点与第三边的中点所连线段之间的位置关系和数量关系，注重从特殊（图1）到一般（图2），即从特殊等腰三角形入手，逐步过渡到任意三角形，当从点A在BC的上方过渡到点A在BC的下方时（图5）（也就是题中两边为斜边向内作等腰直角三角形（图3）），几何属性的结论仍保持不变，有助于引导教师和学生在日常的教学与学习中注意观察与思考相关几何图形的变与不变的属性.本题所考查的知识与能力相当丰富与深奥，如特殊三角形的性质（等腰三角形、直角三角形、等腰直角三角形）、三角形的中位线、平行四边形的判定与性质、三角形全等的判定与性质、平行线的性质等，试题巧妙地设置“操作发现”、“数学思考”、“类比探究”由易到难的三个层次.在“操作发现”中，设置一些简单的补充说明文字与判断选项题，起点低，入口宽，让学生作出分析与思考后直接进行判断，循序渐进地引领学生在观察操作中积累一定的数学活动经验及简单逻辑推理；在“数学思考”中，通过背景图形的变化（从特殊等腰三角形，逐步过渡到任意三角形），将数学问题的特殊性拓展到一般性、普遍性，进行推广与应用，由直觉感观逐步上升到理性思考，要求学生运用所学知识进行分析、综合、探究与求证；在“类比探究”中，进一步将问题推向一个新的高峰与推理.该几何压轴试题也饱含命题者的良苦用心及对广大学生的人文关怀，如在“操作发现”中的特殊图形的相关辅助线示范、补充与提示，由易到难的层次的设置，相关几何图形由特殊到一般的变化过程，几何图形性质的不变性等，都给了学生很好的启示、引领与水到渠成的提示.

“横看成岭侧成峰，远近高低各不同”，在试题研究和课堂教学中，如果我们能以三角形、四边形等基本图形为背景，以相关边长或某些线段的长作正多边形，借助相关点动，带动背景图形（三角形、四边形等）的变化，相关图形之间的位置、形状与大小关系却依然保持着某些结论的变与不变的属性，给我们增添无穷的趣味性、想象力和探究力.

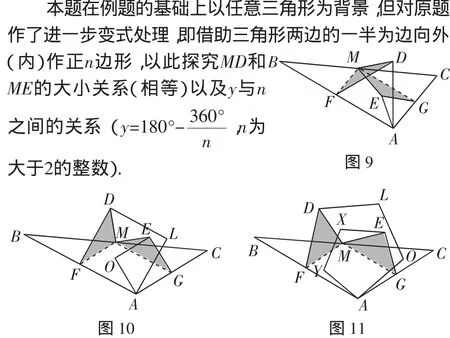
拓展1：在任意△ABC中，F、G、M分别是AB、AC、BC的中点，分别以AF、AG为边向外作正n边形（n为大于2的整数），如：正三角形ADF，正三角形AGE（图6）；正方形AFDL，正方形AGEO（图7）；正五边形AFDLO，正五边形AGEXY（图8）；……，∠EMD=y.

（1）探究MD和ME的大小关系；

（2）写出y与n之间的关系；

（3）当点A位于BC的下方时（即向内作正n边形，如图9、图10、图11），（1）和（2）中的结论是否依然成立？

拓展2：以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE，连接EB、FD，交点为G.

（1）当四边形ABCD为正方形时（如图12），EB和FD的数量关系是_________.

（2）当四边形ABCD为矩形时（如图13），EB和FD具有怎样的数量关系？请加以证明.

（3）四边形ABCD由正方形到矩形到一般平行四边形的变化过程中，∠EGD是否发生变化？如果改变，请求出∠EGD的度数.

本题在例题中三角形的基础上拓展：以动态特殊四边形为背景，以一组邻边为边向外作等边三角形，酝酿与构建从特殊（正方形到矩形）到一般（平行四边形），以此进一步类推，以这组邻边为边向外作正n边形，始终保持相关图形之间位置、大小、形状之间的变与不变的几何属性（线段之间的数量关系及所夹角度）.

拓展3：如图17～19，以矩形ABCD的边AB、AD为边分别向内侧作等边三角形ABF和ADE，连接EB、FD，它们相交于点G或它们的延长线交于点G.∠EGD是否发生变化？并求出∠EGD的度数.

解析：以矩形ABCD的边AB、AD为边分别向内侧作等边三角形ABF和ADE.当点G在线段FD的延长线上（如图17）时，∠EGD=60°.当点G在线段FD（如图18）或DF的延长线上（如图19）时（但点G不在线段EB或EB的延长线上），∠EGD=120°.

拓展与延伸中考题或几何素材，对老师而言是开发有限的教材资源、创造性地使用试题素材的举措之一，对同学们而言是研究性学习的一种有效的方法，不仅可以帮助自己更好地理解知识间的内在联系，而且可以培养探索数学规律的能力，达到整合知识的目的.同学们运用自己探索发现出来的规律或结论解决问题时，不仅会产生一种成就感，而且会提高对数学这门课程的兴趣，在试题的拓展中领会分析问题、解决问题和探究问题的方式、方法，进一步增强学习的主动性、积极性.

用我们教师的无限的智慧与辛勤的汗水，将中考试题的变式、拓展播撒在我们的课堂，让我们的学生在试题拓展的课堂中自然体验试题的独特风韵、新中考的清新容颜.把数学之妙、数学之思、数学之用、数学之美展现在我们精心设计的题组里，让学生尽情起舞，从容地面对更高、更远的天空，把梦想与希望放飞，成就人生的精彩.

1.卜以楼.一个几何模型在中考试题中的拓展与延伸［J］.中学数学（下），2010（6）.

2.吴永刚，董建功.从“无从下手”到“别有洞天”——对一道中考几何题的研究［J］.中学数学（下），2009（9）.

3.喻汉林.中考数学命题创新的意义与方法［J］.试题研究，2003（2）.

4.曹经富.立足教材习题 注重知识延伸［J］.中国数学教育（初中），2012（7）.

5.曹经富，刘荣坚.与三角形、四边形有关的变换操作题赏析［J］.中国数学教育（初中），2012（6）.