自主订正：知识“内化”的重要途径*

☉江苏省如皋市江安镇滨江初级中学 周文斌

自主订正：知识“内化”的重要途径*

一、写在前面

☉江苏省如皋市江安镇滨江初级中学 周文斌

在学生学习的各个阶段，充斥着各种各样的考试，很多考试都是为了对学生前一阶段的学习状况进行“摸底”.在这些考试中，学生出错是不可避免的.这些错误的生成原因是多样的，有些是学生的认知缺陷所致，有些是学生的解题“陋习”所致.适时讲评可以弥补学生认知的缺陷，适量训练可以矫正学生的解题“陋习”.但是，无论是知识的“补缺”，还是“陋习”的矫正，都必须通过学生的自主订正来实现.自主订正非常重要，它是学生知识“内化”的最重要的途径.本文拟结合一次检测讲评课中的“自主订正”的设计谈谈个人对此的感悟，以期对您有所帮助.

二、一次试卷讲评课的“自主订正”设计

（一）测试背景

本次测试安排在中考一轮复习之后，主要是对前一阶段复习的一个总结与提升，同时通过“弥补缺陷”为下一阶段的复习做好铺垫.本次考试，考查了前一阶段的一些基础知识和基本技能，涉及初中数学的很多核心知识，当然一些常见的数学思想和活动经验也渗透在试题之中.全卷共27大题（35小题），满分150分，其中选择题10题，填空题8题，解答题9题.在试题编排时，将选择题、填空题的最后一题，解答题最后一题（主要是第3小问）设置为全卷的“压轴点”，以此来控制满分；选择题、填空题余下的题目和解答题的前6题难度很低，学生解答较为容易，有部分考题甚至是“送分题”，学生基本不会出错；解答题的后三题共26分，难度中等，有一定的区分度，中等学生基本能完成解答，但在解题中会出现失误.

（二）“自主订正”时的设计及分析

1.试卷讲评前

教学设计：

请同学们将4～9，11～17，19～24，27（1）中出错的题目自行订正，将这些题目中用到的知识、方法及数学思想梳理一下，写在题目的旁边.这些题目中没有出现错误的同学，订正自己出错的其他题目.

部分试题呈现：

第26题 如图1，在Rt△ABC中，∠C=90°，BD平分∠ABC，DE⊥BD交AB于点E，⊙O是△BDE的外接圆，交BC于点F.

（1）求证：AC是⊙O的切线.

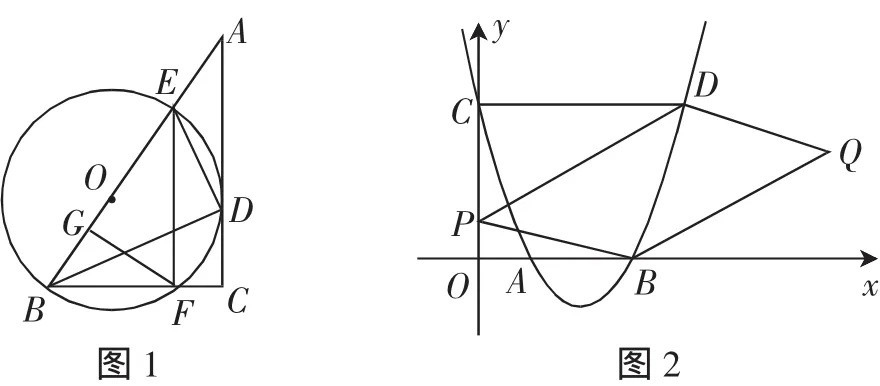
第27题 如图2，已知二次函数y=x2+bx+c的图像与x轴交于A，B两点，交y轴于点C，过点C作CD⊥y轴交该抛物线于点D，且AB=2，CD=4.

（1）该抛物线的对称轴为______________，B点坐标为____________，CO=___________.

设计意图：在讲评之前，选择了三类题目让学生自主订正：第一类，计算错误的，如第19题，同学们都能用待定系数法列出方程组，但解方程组出现了计算错误；第二类，读题不清，如少数同学解答第22题时没有求出整数解，解答第27题第（1）题时没能将数与形进行简单的结合；第三类，个案错误，如第4题只有两个同学出错，第26题第（1）问有6位同学出现问题.这些试题，难度较低，解答出错的学生不多.当给他们自己再度审视试题的机会时，他们一般都能给出正确的解题过程.于是，笔者将这些题目拼在一起，让学生能在短暂的时间内将解答中出现的“问题”化解，为接下来的小组交流和全班交流赢得时间.

2.小组交流后

教学设计：

先在学习小组中交流：10，18，25，27（2），理清本组同学解题中出现错误的原因，找到正确的解题方法，并将这些试题涉及的知识梳理一下，然后自主订正.

在学生交流时，教师巡视课堂，并参与小组交流，对学生解题中出现的典型错误进行点评，对学生在小组内交流后仍然存在的“困惑”进行即时解答.

部分试题呈现：

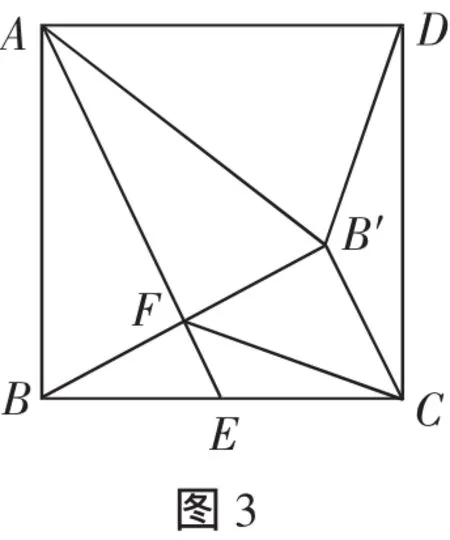
第10题 如图3，在正方形ABCD中，点E为BC边的中点，点B′与点B关于AE对称，B′B与AE交于点F，连接AB′，DB′，FC.下列结论：①AB′=AD；②△FCB′为等腰直角三角形；③∠ADB′=75°；④∠CB′D=135°.其中正确的是（ ）.

A.①② B.①②④ C.③④ D.①②③④

第27题 （2）若P为线段OC上的一个动点，四边形PBQD是平行四边形，连接PQ.试探究：

①是否存在这样的点P，使得PQ2＝PB2＋PD2？若存在，求出此时点P的坐标；若不存在，请说明理由.

设计意图：这些是中等难度试题，有一定的区分度.从试卷分析的情况来看，考试时只有部分学生给出了正确的解题过程，失分很多.通过对学生解答情况的详实分析，笔者发现学生出现的这些错误，很多是因考试时思维的“暂时性短路”所致.这主要是由于学生知识网络的建构不到位所致.因此，在教学中，我们可以通过小组交流来推动学生认知网络的完善，让学生在交流中实现知识的关联与融合.基于此，笔者将这类考题列入“先小组交流，后自主订正”之列，通过小组内的充分交流，有效梳理解答问题中的“共性错误”，分享全组成员的解题经验，获得正确的解题方法.在小组交流后，对这些题进行自主订正，能将学生在小组交流中的收获迅速“内化”，弥补认知的不足，促进知识网络的完善.

3.全班交流后

教学设计：

通过师生互动对话，在全班交流27题第（2）问的第②小问，将解决这一题用到的知识、方法、数学思想进行彻底梳理，并对同学中出现的各种失误进行了集中点评，交流正确的解题思路和解题方法.在此基础上，要求学生自主订正.

部分试题呈现：

第27题 （2）②当PQ长度最小时，求出此时点Q的坐标.

设计意图：本题是全卷的压轴题，难度较大，全班只有一个学生给出了正确的答案，大多数同学只给出了部分解题环节，有少数学生未对本题进行任何解答.对此题采用全班交流的形式，意在通过师生的互动对话，明晰本题的解题思路，梳理知识应用中的技巧，呈现涉及的数学思想.对这些方面的即时点拨，能让学生深入感知本题的考试意图，体验到初中数学核心知识在解题中的“应用价值”，从而获得问题解决的基本方法，归纳整理此类考题的通用解法，为接下来的自主订正和再度应用做好铺垫.

三、教学感悟

1.分段实施，强调过程体验

无论是阶段性考试，还是本文中所述的中考前的模拟考试，试题的编排都必须遵循学生的认知规律.一份试卷，试题的分布应符合“教学常态”，难易题的分布要合理，既要有多数学生能够解答的“基础题”，也要有只有少部分学生能够解决的“压轴题”.就算是同一道考题，不同分支也因承载着不同知识的考查任务，而使其难度不尽相同.事实上，“多问”考题一般梯度都很明显，难易度非常清晰，小题之间具有明显“关联”，难度随着题号不断增加.因此，在安排学生自主订正时，教师应根据试题的难易程度和学生的解答状况对试题进行组合，根据不同的教学进程，实施分段订正.通过分段订正的实施，让学生充分体验解题的过程，在自我的主观感悟中，“品味”错误，找到正确的解题路径，实现纠错与提升的双重教学成效.

2.重在点拨，提升内化成效

学生在考试中出现的解题错误，很多是在特定时段内解题思路不畅通所致.在经历了知识学习和适量训练后，解题出现短暂的知识融合困难是不可避免的.这些“困难”是暂时的，主要成因不是知识的不足，而是知识网络建构不到位.因此，在自主订正前，我们可以通过学习小组或全班交流，在师生互动、生生互动中对解题思路进行必要的点拨，帮助他们将已有知识与试题情境进行关联，从而点破他们考试时的困惑，为他们“指点迷津”，让他们“豁然开朗”，进而带着愉悦与兴奋的心情将交流的成果转化为订正的成果.这些适时的互动点拨，让学生将解题中的犯错经验以及错误试题涉及的知识、技能、思想方法和经验“内化”为自己的东西，为今后的解题提供可以借鉴的宝贵经验.

3.分层落实，确保纠错实效

让每一名学生学有所获，是每一节数学课的教学任务，试卷讲评课也不例外.课前，在对“自主订正”进行设计时，我们也应认真分析每一名学生的考情，让他们在讲评课上均有所获.要特别注意的是，绝不能将所有学生都置于同一个能级上进行订正设计.必要时，应该对学生或试题进行适度分层，让每一位学生订正自己能订正的试题，从而解决“吃得了”与“吃得饱”的问题.这种设计理念，在上面的案例中有着明显的体现.如对“讲评前”的自主订正提出了“这些题目中没有出现错误的同学，订正自己出错的题目”的要求，这实际上解决了一部分优等生的“无事可做”的问题，让他们在后进生自主订正时段内，能思考自己的“问题”，提前进入自我反思和自我提升的阶段.这样的教学设计，为优等生积累了小组交流和全班交流的“素材”，让他们能在交流中尽情发挥，以提高其认知的水平和解决问题的能力.

四、结束语

在考试中，学生出现错误是正常的.对教师来说，处理好学生出现的这些错误是试卷讲评课的一个重要任务.通过这些错误实现学生认知的“查漏补缺”，应该是试卷讲评的一个重要任务.那么，如何实现“补缺”的任务呢？笔者认为，自主订正是一剂最为有效的“良药”.通过对不同教学时段的“自主订正”的巧妙设计与实施，每一名学生都能在自主订正中做好“过错”反思，化解“错误”，找到正确的解题方法.毋庸置疑，在订正的过程中，学生的认知会随着订正的进程不断攀升，知识技能、思想方法等都会得到大幅度的提升，这些对学生解决问题能力的提升都是十分有益的.

以上是笔者试卷讲评课上“自主订正”环节的一些做法和思考，不足之处，欢迎各位同行批评指正.

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

2.印冬建.浅谈试卷讲评必须抓住的几个“要点”［J］.中学数学（下），2013（2）.FH

*本文为江苏省南通市教育科学“十二五”规划立项课题“农村初中小班化教学中复式分组的实践与研究”（编号：NT2011361）的研究成果.课题主持人：印冬建，本文作者系该课题组成员.