一道阅读理解题的测后讲评及教学反思

☉江苏省南京市第29中教育集团致远校区 朱玉祥

一道阅读理解题的测后讲评及教学反思

☉江苏省南京市第29中教育集团致远校区 朱玉祥

进入初三后，学校举行了第一次月考.月考范围是苏科版义务教育课程标准实验教科书数学九年级上册第1、3、4章，其中第4章的一元二次方程的应用问题不考.具体内容为图形与证明（二）、二次根式、一元二次方程及其解法.

月考目的明确，重点考基础.学校要求试卷的难度在0.8左右，实际考下来，难度为0.72.试卷的压轴题是阅读理解题型，内容为用配方法求代数式ax2+bx+c（a≠0）的最值问题，并用于实际问题的解决.题目有3个小题，共6分，按1∶1∶4配分.一般来说，求最值问题属于二次函数的内容，如果此题放在二次函数后考，学生理解起来就容易些.但是，作为一元二次方程配方法的拓展，作为能力的测试，提前考一考学生也是可以的.结果分析，此题的得分率接近0.4，与学情较为吻合.可见，大多数学生对用配方法求代数式的最值的理解还存在明显的困难，有必要重点讲评.讲评的价值在于，它对完善学生对配方法的认识有利.

一、试题分析

1.题目

配方法可以用来解一元二次方程，还可以用来解决很多问题.例如：

因为3a2≥0，所以3a2+1就有最小值1，即3a2+1≥1，只有a=0时，才能得到这个式子的最小值1.同样，因为-3a2≤0，所以-3a2+1有最大值1，即-3a2+1≤1，只有a=0时，才能得到这个式子的最大值1.

（1）当x=______时，代数式2（x-1）2+3有最______（填写大或小）值，为_____.

（2）当x=______时，代数式-2x2+4x+3有最______（填写大或小）值，为______.

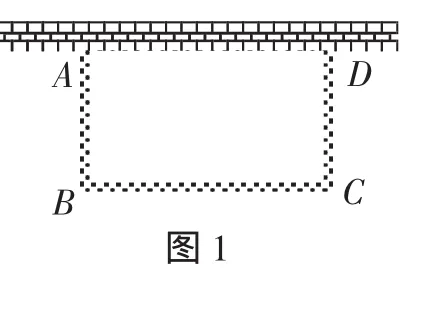
（3）如图1，矩形花园的一面AD靠墙，另外三面所围的栅栏的总长度是16 m，当花园与墙垂直的一面AB长为多少时，花园的面积最大？最大面积是多少？

2.得分情况

以笔者所教两个班为例，此题的得分率甲班是0.32，乙班是0.53.甲、乙两班，一是普通班，一是提优班，两班均分在相应层次班中都是最高.由此可见，整个年级压轴题的答题情况也大致如此.

3.几种错误解答

（1）、（2）两题的错误五花八门，就不一一列举了.主要问题是学生不能理解题意，对“最大”、“最小”随意判断，特别是小题（2），学生不经过配方就下判断，比如填写成“当x=0时，代数式-2x2+4x+3有最大值，为3.”

小题（3），学生的主要错误有如下3种.

（1）用列表法寻找答案.

解：设AB的长为xm，则BC的长为（16-2x）m.

根据题意，得S=x（16-2x）.

因为x＞0，16-2x＞0，所以0＜x＜8.列表：

x/m 1 2 3 4 5 6 7 S/m2 14 24 30 32 30 24 14

从表格可以得到，当x=4时，S最大，最大值是32.

所以AB长为4 m时，花园的面积最大，最大面积是32 m2.

（2）套用小学学过的结论.

解：设AB的长为xm，则BC的长为（16-2x）m.

（3）只见配方之“形”，却无配方之“实”.

解：设AB的长为xm，则BC的长为（16-2x）m.

根据题意，得S=x（16-2x）=-2x2+16x.

因为-2x2≤0，所以-2x2+16有最大值16x.

即-2x2+16x≤16x，当x=4时，-2x2+16x的最大值是32.

所以AB长为4m时，花园的面积最大，最大面积是32 m2.

二、讲评环节与简述

1.讲评环节

试题讲评，不仅要让学生知其然，还要让学生知其所以然；不仅要让学生懂得题目的正确解法，还要让学生明白错误解法究竟错在何处.目标是：讲评后，学生恍然大悟：原来这样做！

经过一番思考，压轴题讲评大致按下面的几个环节进行.

（1）让学生讨论：阅读理解题要我们阅读什么？理解什么？题目在暗示我们什么？

（2）展示错题，让做错的学生谈谈他们的解题想法，并组织辨析.

（3）请解答正确的学生讲题，并谈解题体会.

2.讲评简述

环节1：呈现压轴题.

教师问：这是什么题型？

学生集体回答：阅读理解.

教师继续问：既然是阅读理解，那当然要好好阅读，好好阅读就是带着“理解”的目的去读.请同学们谈一下阅读的体会.

学生1：我的体会就是首先要把题目仔细地读一遍，看看题目都说了什么，可是，我知道题目在说什么，但就是没懂啥意思，所以，这题我没做对.

教师引导：阅读题目除了要读明白题目说了什么，还要看题目要解决什么问题，怎样解决问题.边看边把关键词用笔划下来，以提醒解题时注意.现在来读第一句话，看看这句话传递着什么信息.

学生2：第一句话告诉我们用配方法不仅可以解一元二次方程，还能解决其他问题.

教师点评：不错.第一句其实就是传递着“配方法可以解决新的问题”的信息，同时也暗示我们解决所给新的问题要用配方法.所以，读了这句话，就该把“配方法”3个字划下来，以引起注意.如果谁用其他方法解决问题，那么他首先就犯了理解的错误.

数学阅读题，往往就是给出一个概念，或给定一个方法，然后我们就要用它所给的概念或方法解决问题.一般来说，题目中还会举几个例子，具体示范怎么用给定的概念或方法，那么阅读时就要用心去体会，解题时谨慎去模仿（不仅形似，还要神似），并注意沿用同样的思路和方法.

教师引导：大家继续看题目中的“例如”，这里给出了如何判断配方式的最大值和最小值的方法.

学生3：我就是这儿没读懂.主要是对3a2+1后面的1为什么是最小值，而-3a2+1后面的1却又是最大值，没有弄明白.

学生4：我有点懂.在3a2+1中，3a2的值越大，和就越大；3a2的值越小，和就越小.因为3a2没有最大值，只有最小值，所以，当3a2=0，也就是a=0时，3a2+1的值就最小，最小值是1；而-3a2没有最小值，只有最大值，所以，当-3a2= 0，也就是a=0时，3a2+1的值就最大，最大值是1.

教师赞赏地点评：学生3说得很好，最大值、最小值的判断不容易理解.不过学生4解释得很好，两个数相加，一个加数不变，另一个加数的大小就决定了和的大小，关键看另一个加数究竟能取到最大还是最小，如果能取到最大，则和就最大；如果能够取到最小，则和就最小.当然，这个问题还需要再深入理解.

老师引导学生关注“例如”中两个式子中的平方项.经过讨论、争辩，学生知道了a2前的系数的正负能决定和的值的最大或最小，若系数是正数，比如3，3a2+1就有最小值；若系数是负数，比如-3，-3a2+1就有最大值.这样判断既容易又快速.

但从讨论中发现，很多学生对3a2+1和-3a2+1是配方式并不理解，认为3a2+1与-3a2+1并没有经过配方，甚至有学生还考虑过该如何对3a2+1和-3a2+1进行配方.笔者在黑板上写道，式子3（a-0）2+1和-3（a-0）2+1是不是配方式？学生谨慎答道：是.或许学生觉得这么写还是有点别扭，但觉得它很“像”配过方的式子.笔者告诉学生，一般配方式形如a（x-h）2+k，而3a2+1和-3a2+1其实就是3（a-0）2+1和-3（a-0）2+1，3或-3相当于一般配方式中的a；在3a2+1和-3a2+1中的a和1就相当于一般配方式中的（x-h）和k，只是h=0而已，所以，3a2+1和-3a2+1本身就是配方式.只有这样理解，我们才能把“例如”中的思想方法迁移到题（1）和题（2）中来，比如题（1）中的代数式2（x-1）2+3就是一个标准的配方式，回答起来容易些；而题（2）要通过配方化为a（x-h）2+k，才可解决问题.

学生5：我知道要配方，但就不知道代数式-2x2+4x+3怎么配方.一元二次方程配方，是在“=”两边同时除以二次项系数，然后把常数项移到“=”右边，再在“=”两边同时加上新的常数项，可是-2x2+4x+3后面没有“=”，更看不到有“=”右边的0，没有办法“同时除以”，也没有办法“同时加上”，当时就觉得题目有问题，所以无法解答.

这正是题（2）答得比题（1）差的主要原因.根据教科书提供的解一元二次方程的配方方法，都是在“=”两边进行的，所以，学生遇到没有等号的二次式就束手无策了.有的学生只好直接答最大值是3.

教师请做对的学生展示一下正确的配方，并谈配方的体会.

学生6：（投影正确配方结果之后）我是想，二次项的系数要变成1，在方程两边可以同时除以二次项的系数.但在代数式中就不行了，只能“提”出来，否则就改变原来代数式的值了.配新的常数项也一样，必须加一项再减这项，否则也会与原式不等.

学生这才明白，代数式的配方要在一边进行，而且也可以在一边完成.给代数式配方的策略是“提”二次项系数，而不是除以二次项系数；是加上新常数项再减这个新常数项，而不是在等号两边“同时加”.

教师给出结论：对一般配方式a（x-h）2+k：若二次项系数a＞0，a（x-h）2+k有最小值，当x＝h时取得最小值k；若二次项系数a＜0，a（x-h）2+k有最大值，当x＝h时取得最大值k.特别地，若a＞0，配方式ax2+k有最小值，当x＝0时，ax2+ k取得最小值k；若a＜0，配方式ax2+k有最大值，当x＝0时，ax2+k取得最大值k.

环节2：先展示3种错解，请解答错的学生谈谈解题的想法.

学生6：我是用列表法找最大面积的.因为我觉得只要能找到最大面积就行了，用什么方法都可以.由于以前学过用表格来探讨数的变化情况，所以我觉得用这种方法是可靠的.通过表格，很容易就找到了最大值.可惜没得到分，有点儿想不通.

学生7：因为你没有用配方法.（大家笑）

学生8：列表求最大值不行.因为表中只列出x取整数时对应的x（16-2x）的值，是不全面的.因为并不是所有的代数式都是在x为整数的时候才有最大值，所以，用列表法来找最大值不可靠.

教师点评：学生8讲得对，表格中只列出了几对特殊值，当x取3.9或4.1时，表格中并没有列出它们对应的值，也就无法判断这些对应值是不是比32要小，所以，说32是最大值理由不充分.所以，表格法不能解决代数式值的最大或最小问题.并且列表法也的确不符合题目规定的解题要求.

学生9：我是用小学学过的一个结论来做的.但就是没有搞清楚围成4边和围成3边的区别.其实做的时候我就没有把握，只是因为我不知道怎么配方，就只好这样做碰碰运气了.结果真错了.

学生10：其实，不管是围成4边还是围成3边，用小学学过的结论都能得到结果.比如总的长度为16，用16除以4得4，如果围4边，边长为4的正方形面积最大；如果围3边，宽为4、长为8的长方形面积最大.

教师追问：为什么？理由呢？

学生说反正小学就这样做的.

教师指正：对本题而言，指定用配方法解决问题，所以这个结论肯定不能用.不过学生10说的结论是对的.但这个结论在小学用用还行，在中学用就得先获得可以直接引用的“许可证”（需要证明）.所以，在没有“许可”之前，即使题目中没有指定方法，也不要用这个结论.当然，在不需要解答过程的填空题或选择题中是可以用的.

学生11：我用的是第3种方法，我不会配方，就模仿3a2+1与-3a2+1.现在我知道，我的模仿只是“形”似，而“神”不似，根本就不是配方.其实当时我就知道错了，因为我“配方”后却无法计算了.但我知道x的值应该是4，就在后面写了x＝4时，取得最大值32.我那是“投机取巧”，结果还是没取到巧.

环节3：引入正确解法.

教师小结：第1种和第2种方法都没有用配方法，而且解法也有问题，所以是错的.第3种方法虽然想到了配方，但配方配得不对，外形有点像，实质却相差很远.所以，也是错的.这3种方法都说明大家没有理解题意，这是出错的关键.下面看正确的解答.请学生12讲一讲解题的想法.

学生12：（投影正确解法，并解释每一步解答的理由）我主要是理解了题目的要求，知道用配方法解决问题，所以，我就对列出来的表示面积的式子配方，然后学着“例如”的方法判断面积的最大或最小值.这题我拿满分的最大体会就是：题目要多读、多想、多用心揣摩思想方法.

教师：多读、多想很重要.平常大家要读一读概念，读一读定理，还要多读一些例题.读后还要多想，多用心揣摩解题方法，要尝试解题，要通过不断地训练来提高解答“阅读理解”题的能力.

三、教学反思

1.配方法教学要呈现多样化

配方法是重要数学方法.教材在一元二次方程中首提配方法，之后在二次函数中再提配方法.但这两种配方的形式有所不同.一元二次方程的配方（书中例题都是采用这种方法），在标准形式下常利用等式的性质分三步进行，一是把原方程的常数项移到等号右边，二是在等号两边同时除以二次项的系数，把二次项系数化为1，三是在方程两边同时加上一次项系数一半的平方，这时左边就配成完全平方式，右边是常数，接下来就可以用开平方的方法求解了；而二次函数的配方，不能在等号两边进行，而是在二次式的一边先把二次项的系数提出来，然后利用先加后减的方式配上一次项系数一半的平方，最后再转化为标准的配方式.由于这两种方法的不同，导致学生学会了一元二次方程的配方，却不能对一元二次三项式进行配方，就像月考中的压轴题，学生并不能把对一元二次方程的配方方法迁移到对二次式的配方上来.这固然和教学没有讲透配方的本质有关，但更和教学一元二次方程的配方解法的单一性有关.

由此想到，在教学一元二次方程的配方法时，不妨改变配方的形式，或呈现多样化的配方方法，既讲在等号两边的配方方法，也讲在等号一边的配方方法，这样，学生就容易适应二次函数的配方，方法得到统一，过渡就会平稳.

举个例子，在教学配方法解一元二次方程2x2-4x-3= 0时，就可以采用以下两种方法：

两种方法的教学，呈现出配方方法的多样化，一是容易加深学生对配方本质的理解，二是学生对二次函数的配方容易顺利接受.

2.特殊的配方式不可一带而过

一元二次方程的标准形式是ax2+bx+c=0（a≠0），对于标准形式的一元二次方程的配方，学生会按步骤中规中矩地进行，然后得到配方式（x+h）2=k.如果一元二次方程只有二次项和一次项，学生也能从容配方，因为他们能找得到二次项系数化为1后的一次项系数，他们会有依据地配上一次项系数一半的平方，最后还是能得到（x+h）2=k.但对缺少一次项的一元二次方程，比如ax2+c=0（a≠0），学生就不知道如何对待了.因为他们发现，要配的新的常数项的依据“一次项”找不到了，所以，就会觉得无法完成配方.真是“身在此山不识山”.ax2+c=0本身就是配方式，却还在为配方烦恼，怎不让人一声叹息呢.出现这种情况，只能说明在平常教学中，老师没有把特殊的配方式认真地向学生交待清楚，多数情况下是一带而过，所以学生识别不出.

其实这种现象不只在配方中.有的学生竟不知道最简单的一元二次方程可以是x2=0.要求学生写一个一元二次方程，其两根分别是2和-2，有的学生不敢写成x2=4，却要写成2x2-8=0，甚至写成2（x-2）（x+2）=0才放心.在二次函数中，学生能说出y=2（x-1）2-5的图像的顶点坐标，却对说出y=x2或y=x2+1的图像的顶点坐标迟疑不决.这就说明一些特殊式子在教学中也要特别指出，以让学生能判断、会识别.

比如对配方式3x2+1和-3x2+1，在教学中就需要对照一般式a（x+h）2+k给予解释，说明一般式中，若a=±3，h=0，k= 1，那么就可得到3x2+1和-3x2+1，这就是特殊的配方式了.

3.教学中要渗透学生阅读能力的培养

学生阅读理解能力不足，与数学教学中轻视学生阅读有关.比如现在常用PPT教学，容量大，换页快，学生根本就来不及阅读，更多情况下，都是教师直接代替学生阅读，长期如此，学生的阅读水平就难以得到提升.教学中的概念和例题，也都是教师讲解，很少要学生去读内容，去读解答，因此，阅读理解题中的概念、方法及解题暗示，学生难以从中读得出来，这就成了解答阅读理解题的一个障碍.

同样，教学中指导学生阅读更是缺失.一道题目，一个概念，究竟怎样去读才能增加理解，这需要在平时教学中给予渗透式的训练.比如几何题的阅读，就需要指导学生一边读题一边看图，一边看图一边在图上作标记，一边在图上作标记一边想与之相关的内容.每读到一个“形”，就要在图中找到“形”，就要标记“形”的相关条件，就要想到与“形”有联系的一些概念或定理，这样阅读就会增加学生对题目的理解.再比如应用题的阅读，可以指导学生先阅读题目的最后一句，明白求什么，不妨先把要求的“什么”用x表示，也就是设好未知数，然后一边读题一边用笔划下关键字词句段，并把表示未知数的量或与未知数相关的量用x或含x的代数式表示，这样做本身就是尝试理解，题目读完，题意大体就在脑海中成形了.平时对书上的例题，也可以让学生先阅读，包括读解答，教师只须对例题设置一些提问，来检查学生的理解程度，同时可以指导学生对例题解答的每一步计算或推理写出依据，引导学生去理解.笔者认为，例题未必都需要教师去讲，有的时候完全可以让学生先阅读，然后就给出题目让学生根据例题的思路尝试解答，以此方法来培养学生对题目的阅读理解力.

数学教学要有耐性.一味地图快，一味地赶进度，往往会把学生的阅读时间甚至理解数学的时间都挤掉，这对学生的阅读理解能力的提高，甚至对学生整个数学的学习都是不利的.

1.肖世兵.客观题讲评应重视“对而不懂”现象［J］.中学数学（下），2013（8）.

2.王莉.养成好习惯 发挥正能量——浅谈七年级学生良好数学学习习惯的培养［J］.中学数学（下），2013（11）.

3.朱玉祥.“千算万算”离不开“计算”——由中考题中的“计算”说起［J］.中学数学（下），2013（11）.WG