基于动态卡式系数的大型潜水电机偏心特征量的计算

狄 冲，汪 朗，鲍晓华，朱庆龙

（1.合肥工业大学 电气与自动化工程学院，安徽 合肥 230009；2.大型潜水电泵装备技术安徽省重点实验室，安徽 合肥 231131）

大型潜水电机通常作为水泵的动力来源，在国家防治水安全领域发挥着重要作用。由于大型潜水电机一般在特殊工况下工作，并且与人民财产安全息息相关，因此其工作的可靠性问题值得人们重视。作为大型潜水电机，偏心将严重影响其工作的可靠性，因此，分析转子偏心情况下大型潜水电机的各项性能指标就变得尤为重要。

引起转子偏心主要有2个因素：制造加工中的公差和电机轴承的磨损。目前，国内外诸多学者在对转子偏心的研究之中已取得了一系列的研究成果。Kim U和Lieu D K先后建立了永磁电机不考虑开槽效应与考虑开槽效应的偏心模型［1-2］，并且分析了转子偏心情况下气隙磁场的畸变特性。Dorrell D G则提出了一种新型的模型，用来计算由转子偏心引起的轴向不平衡磁拉力，并通过实验验证模型的正确性［3］。Belahcen A研究了转子偏心对电机损耗的影响，并且指出在相同偏心度的情况下，静偏心引起的损耗要比动偏心引起的损耗大［4］；朱海峰等人则采用解析法与有限元相结合的方法计算了在转子静偏心情况下的径向电磁力的分布状况［5］；仇志坚等人则针对标贴式永磁电机转子偏心问题，建立了基于边界摄动法的偏心解析模型，采用解析法计算出了偏心情况下的磁通密度，并使用有限元分析结果验证其模型的有效性［6］。然而，更多的学者将研究重点集中在偏心故障的检测之中。Cameron J R通过传统的磁势磁导解析法计算出了转子偏心引起的气隙磁密谐波，并证明这些磁密谐波将在定子绕组中感应出一定特征频率的电流信号［7］。此外，还有一些文献研究了静偏心（SE）、动偏心（DE）以及混合偏心（ME）情况下其电流检测特征值，以及偏心对电机的影响，并通过一系列实验验证检测技术的有效性［8-12］。

笔者建立转子气隙偏心模型，并且考虑到开槽影响，为了准确计算偏心特征量的幅值，引入动态卡式系数理论，忽略饱和影响、假设线性磁路，应用解析计算的方法得到偏心特征量的幅值解析式，并通过有限元仿真，验证理论的可靠性。

1 理论分析

1.1 转子气隙偏心建模

转子发生偏心时，不管是静偏心、动偏心还是混合偏心，其气隙长度将发生变化。然而，由于电机定、转子两侧都开槽，其气隙将在原有气隙的基础上叠加由开槽引起的“附加气隙”。如图1所示，建立混合偏心情况下气隙长度、定转子几何中心及旋转中心坐标系。

图1 偏心情况下定转子及旋转中心示意Figure 1 Position diagram of rotational center，rotor and stator geometric center under eccentricity

图1中，Os为定子几何中心；Or为转子几何中心；Oω为转子的旋转中心；g为电机正常运行时的气隙长度；δs，δd和δm分别为静偏心度、动偏心度以及混合偏心度。ωr为转子旋转的角速度，其表达式为

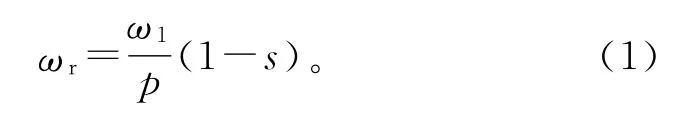
式中 ω1为电源角频率；p为电机极对数；s为转差率。

由几何关系可以得到图1中的混合偏心度以及转子几何中心相对于定子几何中心的角位置：

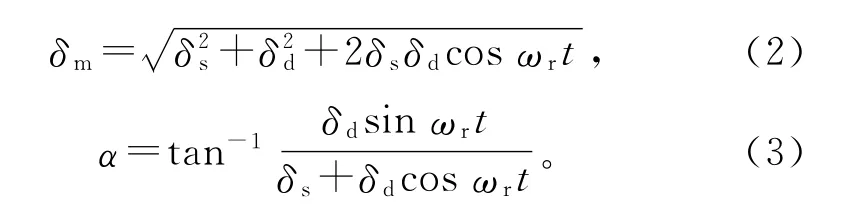
图1中，假设P点为电机定子内表面上任意一点，Rs，Rr分别为定子几何中心和转子几何中心到P点的距离。由几何关系可以得到气隙长度表达式：

电机转子发生静偏心时候，其几何中心与定子中心发生偏移，但其旋转中心仍然与定子几何中心相重合。电机转子发生动偏心时候，其几何中心与定子中心发生偏移，但其旋转中心变为转子自身中心。然而，电机发生混合偏心时候，其转子几何中心与定子几何中心发生偏移，并且产生一个既不是定子几何中心，又不是转子几何中心的新的旋转中心。因此，电机在纯静态偏心和纯动态偏心时候其气隙长度表达式分别为

式（5）为静偏心下气隙长度分布函数，而式（6）为动偏心下气隙长度分布函数。从式（5）、（6）中可以看出，转子静态偏心时候，其气隙长度将偏向某一位置，然后按圆周方向呈余弦分布。然而，转子发生动态偏心时候，气隙长度将是一个随着时间和空间同时变化的二维时空函数。在解析法计算气隙磁密时，笔者应用传统的磁势乘以磁导的方法求取电机气隙磁密表达式。气隙磁导可以表示为

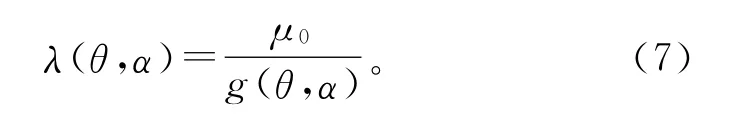
将式（5）、（6）分别代入式（7）中，得到静偏心和动偏心情况下的气隙磁导表达式：

将式（8）、（9）展成傅里叶级数形式［13］，得到

为寻求在静偏心以及动偏心情况下气隙长度的分布规律，由式（5）、（6）可以作出在不同静偏心下气隙长度随定子位置的分布曲线，以及在动偏心下气隙长度的时空分布图，如图2所示，可以看出，转子静偏心情况下，转子向某一位置发展偏移，气隙长度按定子圆周角位置展开后保持不变，不随时间变化，因此，静偏心时候，气隙长度变化是有倾向性的。而转子发生动偏心时，其气隙长度将随着时间和空间的变化而变化，各位置经过一段时间后，其总的平均气隙长度均等，因此，动偏心时气隙长度变化不具有倾向性。

图2 偏心情况下气隙长度分布情况Figure 2 Distribution condition of air-gap length under eccentricity

1.2 偏心情况下的动态卡式系数

以上分析在转子偏心情况下的气隙长度以及气隙磁导的变化函数是假设定转子表面都光滑的情况下而得到的。而实际电机中，一般情况下，定、转子两侧都将开槽。现先考虑电机不偏心情况下定、转子开槽对气隙磁密的变化情况。如图3中所示，假设不开槽时，电机气隙中的磁密幅值为Bmax，开槽后使得气隙中产生一个附加气隙，故磁密幅值将降低，变为Bmin，同时，沿着一个槽距td内的平均气隙磁密降为Bav。对于这种现象，文献［14］引入了卡式系数kc，用来描述因开槽引起的气隙磁密的变化。假设定子开槽，转子光滑时，由定子开槽引起的卡式系数为

从图3中看出，齿边缘处的边缘效应非常显著，其边缘效应作用延续到了槽中心，因此，可知卡式系数与槽深无关。卡特经过保角变换导出了卡式系数的表达式［15］：

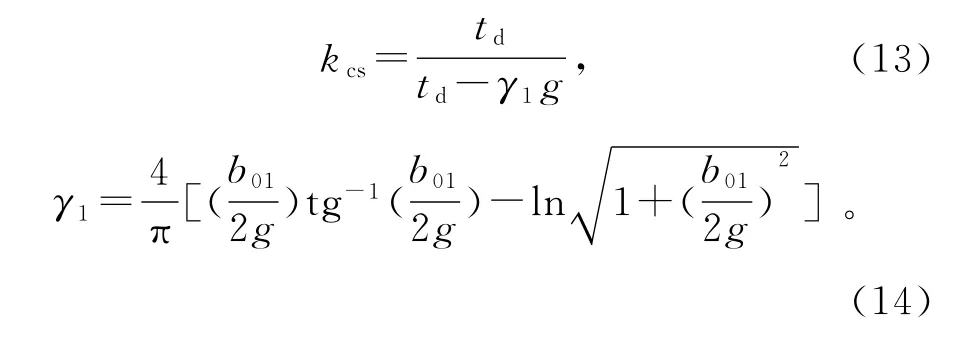
对于定子光滑、转子开槽的情况应将式（13）、（14）中的参数换成相应转子侧的参数。因此，考虑定、转子两边同时开槽的卡式系数可以表示为

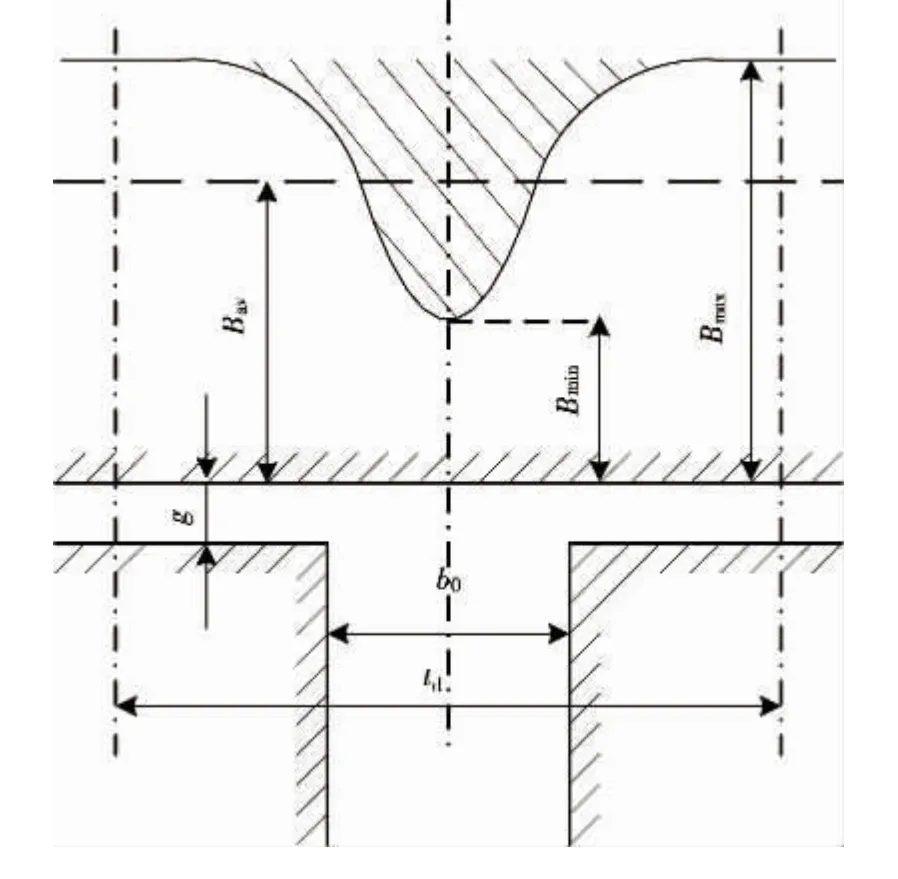
图3 一个槽下的气隙磁密分布示意Figure 3 Distribution diagram of flux density under a slot

该文中涉及的干式潜水电机由于其定子为开口槽，转子为闭口槽，按式（13）、（14）计算时，闭口槽卡式系数等于0，因此，总的卡式系数就等于有定子开槽引起的卡式系数kcs。在偏心情况下，电机气隙长度发生变化，而卡式系数表达式与气隙长度有关，故笔者提出“动态卡式系数理论”，用以描述在偏心情况下各个槽口的卡式系数分布情况。静偏心时，取槽中心线处对应的偏心气隙长度作为计算动态卡式系数的气隙长度，则

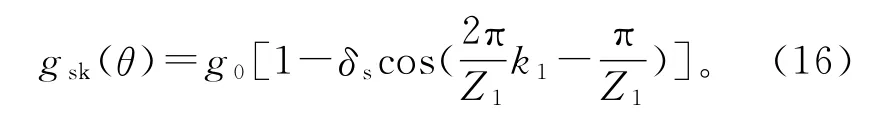
式中 k1为槽号；Z1为定子槽数。比较式（5）与式（16）可以看出，由于静偏心时转子偏向某一位置，因此，槽中心线处的气隙长度与静偏心下气隙长度具有相同的分布状况，如图4所示，可作出静偏心情况下不同槽口的卡式系数分布图。

图4 静偏心情况下不同槽口卡式系数分布示意Figure 4 Distribution diagram of cater factor at different slots under static eccentrictiy

同理，在动态偏心时，槽中心线处对应的偏心气隙长度作为计算动态卡式系数的气隙长度则有

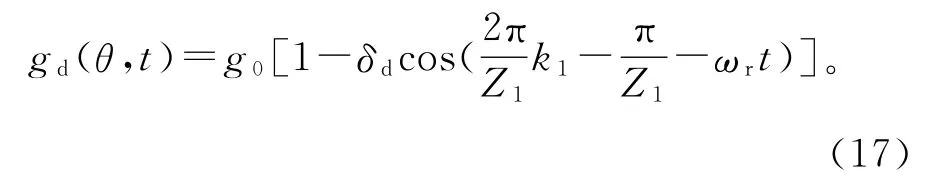
根据式（17），同样能够作出动偏心情况下的不同槽口时空分布的卡式系数图，如图5所示，可知卡式系数与气隙长度具有相同的分布规律。因此，为考虑开槽对气隙磁场的影响，对于式（10）、（11），都需要除以一个动态卡式系数。

图5 动偏心情况下不同槽口卡式系数分布示意Figure 5 Distribution diagram of cater factor at different slots and time under dynamic eccentrictiy

2 偏心磁场特征量的分析与计算

感应电机三相对称绕组通以三相对称电流时，其气隙合成磁场可以表示［16］为

式中 Fp，Fv和Fμ分别表示主波磁势幅值，定子绕组谐波磁势以及转子绕组谐波磁势；φ0，φv和φμ分别为各部分初相角；v和μ分别代表定、转子绕组谐波极对数，其中齿谐波引起的谐波幅值较大，可以表示为

式中 k1，k2都为非零整数。转子μ次谐波相对于定子的角频率为

应用传统的磁势磁导法，可以得到感应电机气隙磁密的函数式，将式（10）中k取1，与式（18）相乘，可得到一系列谐波磁场，其中由静偏心引入的谐波磁密为

观察式（22）～（24），不难发现，转子静偏心新引入的磁密谐波其频率不变，而阶次发生变化，因此，在分析有转子静偏心引入的谐波磁密时，需要通过对气隙磁密按定子角位置作傅里叶分解，从而得到各次谐波磁密的幅值。正常情况下气隙磁密幅值的分布状况如图6所示。

图6为电机正常运行时按定子周向傅里叶分解得到的各次谐波磁密幅值，其中，1次基波和29，31次定子绕组引起的齿谐波具有较大的幅值。分析所用样机为4极电机，定义基波即1次波为p对极波，因此，1，29，31次谐波分别对应2，58，62对极谐波。由理论分析可以知道，静偏心引入的谐波为1，3，57，59，61和63对极的谐波，故应着重关注。笔者将采用有限元以及解析的方法计算引入的谐波磁密幅值，在应用解析法计算时，假设：忽略饱和对磁路的影响；磁路为线性。

通过假设，根据式（22）、（23）可计算出静偏心引入的磁密幅值，并且对于其中的卡式系数，可以求取所有槽对应卡式系数的平均值，如表1所示。

图6 正常运行时各次谐波磁密幅值Figure 6 Air-gap flux density harmonics of a health motor

表1 静偏心下平均卡式系数Table 1 Average cater factor under different static eccentricity

在计算由静偏心引入的谐波磁密时，为方便取57和61对极磁密分别进行有限元计算与解析计算。如图7所示，可以看出，解析计算和有限元计算结果基本一致。在偏心度为0时，有限元计算仍有结果是因为在有限元计算中考虑了饱和效应，而解析计算是不考虑饱和效应的，因此，两者在偏心度为0时有较大差异。

按照同样的方法可以求取动偏心引入的磁密特征量：

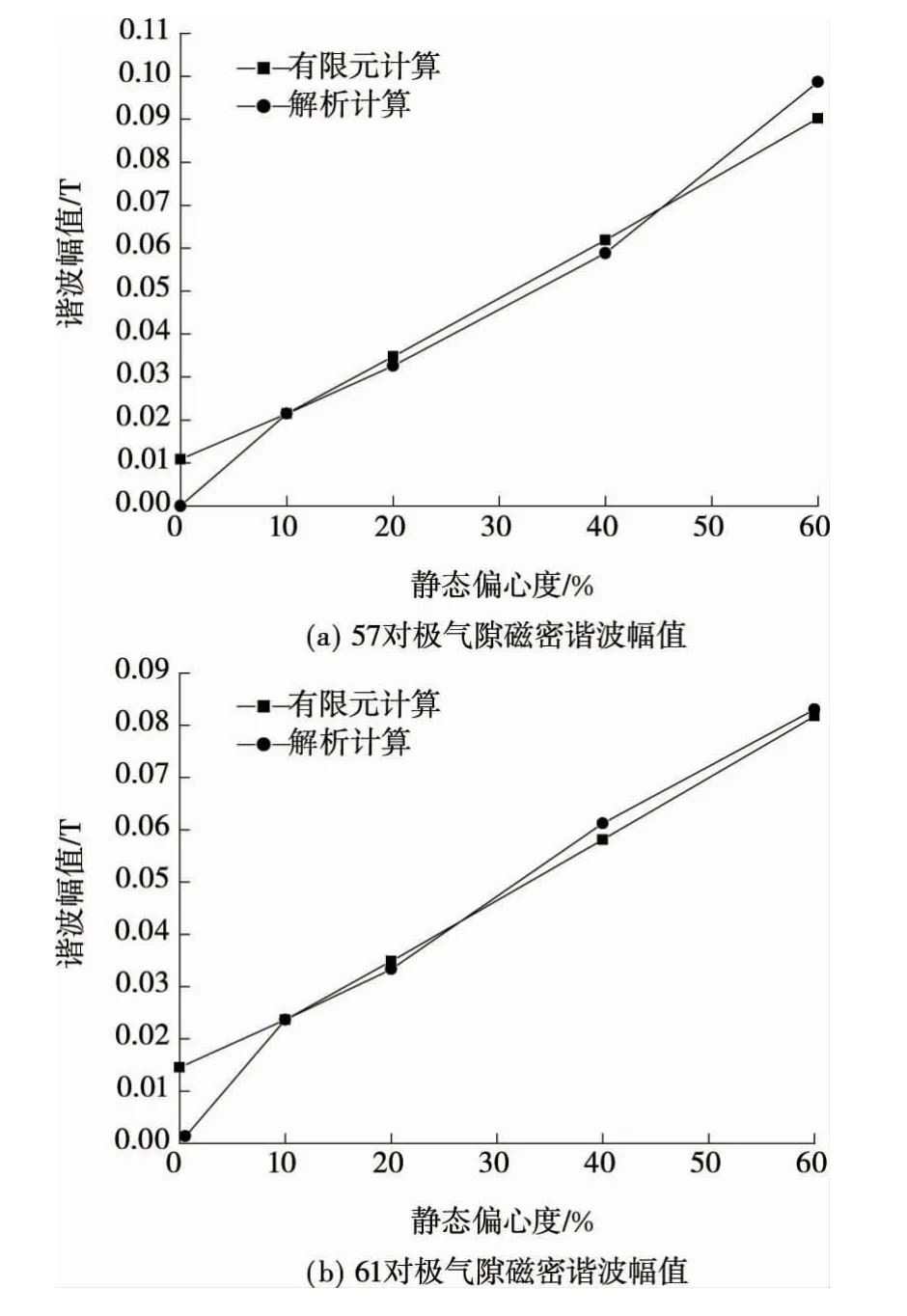
图7 静偏心气隙磁密主要谐波计算值Figure 7 Calculation results of air-gap flux density harmonics under static eccentricity

表2 动偏心下平均卡式系数Table 2 Average cater factor under different dynamic eccentricity

从式（25）～（27）可以看出，当转子发生静偏心时，将引入新的特征频率的谐波磁密，其特征频率为ω1±ωr和ωμ±ωr。在动偏心状态下，实际上各槽的卡式系数随时间变化结果一致，因此，可取某一槽的卡式系数随时间变化的结果求平均值，从而求得动偏心下的平均卡式系数，如表2所示。动偏心引入的谐波磁密如图8所示，25.5和74.5 Hz分别为式（25）、（26）所反映的磁密谐波，这2个谐波是由不同阶次的磁密谐波相互叠加而成，因此，采用一维傅里叶分解难以区别，一般采用二维傅里叶分解来计算。为了简化计算仅分析由式（27）引入的1 227.5Hz谐波。提取图8中的特征频率并计算其不同偏心度下的幅值，如图9所示，可以看出，动偏心引入的谐波磁密幅值非常小，远小于静偏心引入的谐波磁密幅值。因此，可以在静偏心定量计算时重点研究偏心特征量的定量计算。

图8 动偏心磁密特征量Figure 8 Characteristic parameters of flux density under dynamic eccentricity

图9 动偏心气隙磁密主要谐波计算值Figure 9 Calculation results of air-gap flux density harmonics under dynamic eccentricity

3 结语

笔者建立了精确的复杂气隙偏心模型，为研究开槽对气隙磁密的影响，引入了动态卡式系数理论，采用解析法与有限元相结合的方法，分析了动偏心与静偏心引入的偏心特征磁密，并结合动态卡式系数理论定量计算了特征磁密幅值。分析表明，静偏心情况下由于气隙长度不旋转，具有倾向性，其引入的磁密谐波幅值较大，便于作为检测信号用来检测。而动偏心情况下，由于气隙长度始终旋转，因此对各个位置影响是均匀的，其引入的谐波磁密幅值较小，不便于定量检测。该文为今后偏心的定量检测奠定了一定的基础。

［1］Kim U，Lieu D K.Magnetic field calculation in permanent magnet motors with rotor eccentricity：without slotting effect［J］.IEEE Transations on Magnetics，1998，34（4）：2 243-2 252.

［2］Kim U，Lieu D K.Magnetic field calculation in permanent magnet motors with rotor eccentricity：with slotting effect considered［J］.IEEE Transations on Magnetics，1998，34（4）：2 253-2 266.

［3］DorrellD G.Sources and characteristics of unbalanced magnetic pull in three-phase cage induction motors with axial-varing rotor eccentricity［J］.IEEE Transactions on Industry Applications，2011，47（1）：12-24.

［4］Belahcen A.Losses in an eccentric rotor induction machine fed from frequency converter［C］.International Conference on Electrical Machines，Vilamoura，The Portuguese Repubic，2008.

［5］朱海峰，祝长生.转子静偏心时异步电机径向力特性分析［J］.机电工程，2013，30（8）：981-986.ZHU Hai-feng，ZHU Chang-sheng.Electromagnetic racial force analysis of asynchronous motors under static eccentricity［J］.Journal of Mechanical ＆Electrical Engineering，2013，30（8）：981-986.

［6］仇志坚，李琛，周晓燕，等.表贴式永磁电机转子偏心空载气隙磁场解析［J］.电工技术学报，2013，28（3）：114-121.QIU Zhi-jian，LI Chen，ZHOU Xiao-yan，et al.Analytical calculation of no-load air-gap magnetic field in surface-mounted permanent magnet motors with rotor eccentricity［J］.Transactions of China Electrotechnical society，2013，28（3）：114-121.

［7］Cameron J R，Thomson W T，Dow A B.Vibration and current monitoring for detecting airgap eccentricity in large induction motors［J］.IEE Proceeding B，Elctric Power Application，1986，133（3）：155-163.

［8］Nandi S，Bharadwaj R M，Toliyat H A.Performance analysis of a three-phase induction motor under mixedeccentricity condition［J］.IEEE Transactions on Energy Conversion，2002，17（3）：392-399.

［9］Ebrahimi B M，Faiz J.Diagnosis and performance analysis of threephase permanent magnetsynchronous motors with static，dynamic and mixed eccentricity［J］.IET，Electric Power Applications，2010，4（1）：53-66.

［10］Ilamparithi T C，Nandi S.Detection of eccentricity faults in three-phase reluctance synchronous motor［J］.IEEE Transactions on Industry Applications，2012，48（4）：1 307-1 317.

［11］Dorrell D G，Thomson W T，Roach S.Combined effects of static and dynamic eccentricity on airgap flux waves and the application of current monitoring to detect dynamic eccentricity in 3-phase induction motors［C］.International Conference on Electrical Machines and Drives，Durham，North Carolina，USA，1995.

［12］赵向阳，葛文韬.基于定子电流法监测无刷直流电动机转子动态偏心的故障模型仿真研究［J］.中国电机工程学报，2011，31（36）：124-130.ZHAO Xiang-yang，GE Wen-tao.Simulation research of fault model of detecting rotor dynamic eccentricity in brushless DC motor based on motor current signature analysis［J］.Proceedings of the CSEE，2011，31（36）：124-130.

［13］Faiz J，Ardekanei I T，Toliyat H A.An evaluation of inductances of a squirrel-cage induction motor under mixed eccentric conditions［J］.IEEE Transactions on Energy Conversion，2003，18（2）：252-258.

［14］海勒尔，哈马塔.异步电机中谐波磁场的作用［M］.北京：机械工业出版社，1980.

［15］陈永校，诸自强，应善成.电机噪声的分析和控制［M］.杭州：浙江大学出版社，1987.

［16］陈世坤.电机设计［M］.北京：机械工业出版社，2000.