焊管内裂纹电磁激励红外无损检测数值模拟

李龙波，李国华，邢 亮，侯苏灵

(中国矿业大学(北京)机电与信息工程学院，北京100083)

1 引言

直缝焊管就是将热轧板卷成型后，使钢卷变形为圆筒状，用高频电流使管坯融化，在挤压作用下，融化两边熔合在一起，经冷却达到焊接的效果，形成钢管，然后刮去焊缝的外毛刺，再经过定径、矫直、定尺切断;直缝焊管以成本低、效率高、壁厚均匀等特点，广泛应用于石油天然气输送、低压水煤气输送、矿用流体输送和汽车传动轴等方面，特别在石油管道中已经逐步取代不锈钢管;当然，对直缝焊管检测方法的要求也越来越高，而当前直缝焊管内部裂纹的检测方法包括超声波和射线探伤;但超声检测存在检测盲区，检测效率低，缺陷很难定性;射线检测检测存在安全隐患。

与传统方法相比，电磁激励红外热像无损检测用红外热像仪测取目标物体表面的红外辐射能，并将其转变为直观形象的温度场，通过观察该温度场的均匀与否，来推断目标物体内部是否有缺陷［1］;其在焊缝缺陷上的检测也越来越得到重视;国内红外热像无损检测技术的研究刚开始［2－3］，以电磁为激励源的红外无损检测的研究少之又少［4］，国外对此研究也不多［5－9］，需要对其进行研究和完善。

2 仿真有限元模型

2.1 感应加热有限元理论

2.1.1 电磁场数学模型

感应加热的过程是电磁场中能量传播的过程，电磁场中的直缝焊管由于电磁场的作用感生涡流而产生热量，描述电磁场分布和传播的数学方程就是麦克斯韦方程组，其积分形式为:

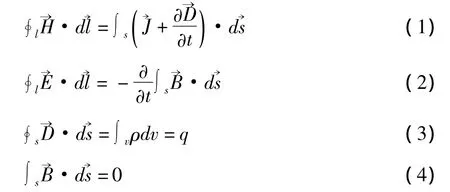
2.1.2 温度场数学模型

求解涡流场的目的是利用求得的感生电流焦耳热作为内热源来计算温度场，温度场的计算结果可以用来分析感应加热过程中直缝焊管裂纹上方的温度变化情况，为内部裂纹可检测性评判提供依据。

对于直缝焊管，根据能量守恒定律，圆柱坐标系下的固态导热微分方程［10］为:

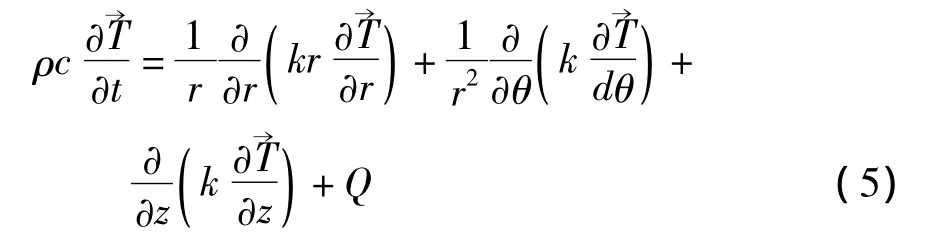
式中，珗T，ρ，k，c，Q 分别为试件的瞬态温度、密度、导热系数、比热、内热源生成的热量。

故本文中计算温度场的数学模型为:

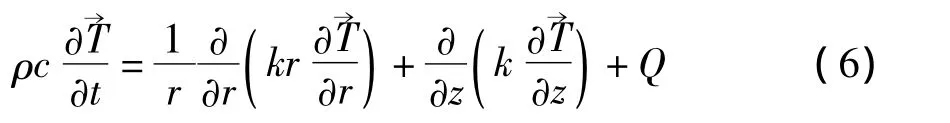
设直缝焊管和外界空气初始温度的初始温度为300 K，对流系数设为15 W/(m2·K)，根据热传导第三类边界条件可得:

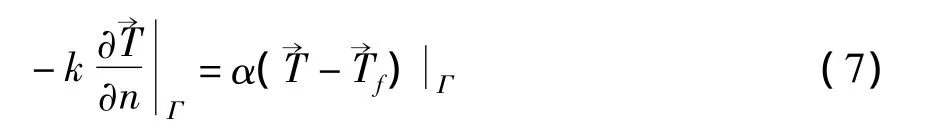
式中，k，n，α，珗Tf，Γ 分别为试件的导热系数、边界上的法向向量、对流系数、空气温度、试件边界。

2.2 直缝焊管有限元模型

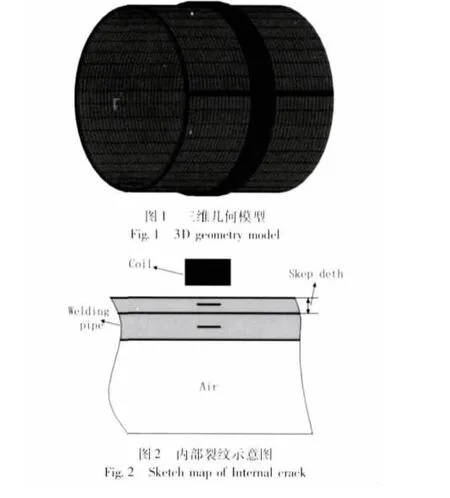
本次仿真以20钢为研究对象，ANSYS中电磁分析选用3－D棱边法，直缝焊管内径100 mm，壁厚4 mm，长度200 mm;焊缝宽1.9 mm;激励线圈为铜线圈，位于裂纹正中，内径为110 mm，壁厚1 mm;裂纹长度为8 mm，宽0.25 mm，深度0.6 mm，如图1所示;焊管、焊缝、热影响区、线圈和空气的网格单元采用SOLID236单元;热分析采用SOLID90单元;为确保仿真精度，直缝焊管内充满空气，管外除线圈皆为空气物理参数如表1所示。

内部裂纹在电磁激励直缝焊管中的位置分为两种:位于趋肤深度深度以内的隐藏裂纹、位于趋肤深度以下的内部裂纹，如图2所示。

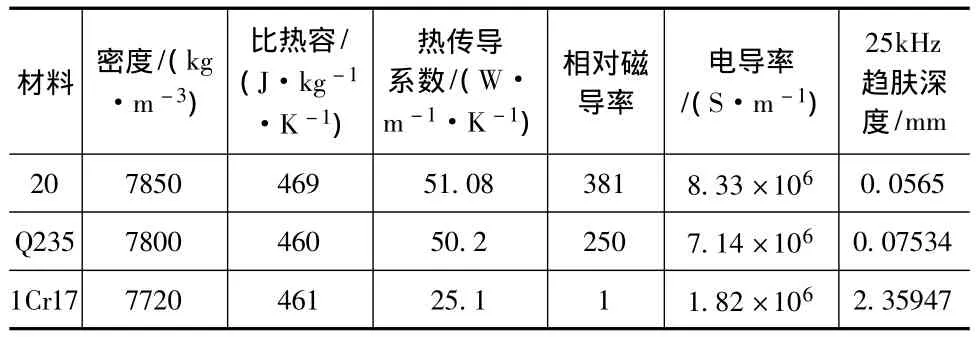
表1 不同材料物理性能Tab.1 Physical properties of different materials

3 评判标准

3.1 温度分布图

为了使模拟仿真更好的向实践中推广，选择了热灵敏度0.04℃，帧频60 Hz的红外热像仪，亦即在温差＞0.04℃的情况下，红外热像仪会以每秒60张的热像图显现出来;图3为无缺陷表面温度云图，只要出现如图4所示的温度图，我们就可以判定焊缝此处存在内部缺陷，因此在仿真模拟中两点的选取至关重要;如图3、4温度云图所示，以缺陷中心为原点，平行于焊缝为X轴，垂直焊缝为Y轴，温度分布都是以缺陷为中心温度最高，向两边下降;无缺陷时，Y轴(垂直焊缝方向)温度分布均匀。

3.2 温差参考点的选取及评判指标

本次仿真激励频率为 25 kHz，电流强度为8 A/mm2，加热时间为 1 s，散热时间 2 s，选取裂纹上方表面中心点为固定点A，向Y轴方向90°圆环上选取40个点，其中焊缝21个点，母材19个点，得到A点与参考点最大温差分布图以及离中心最近最大温差点B，为了消除随机性，以固定A、B两点处所有节点的平均值之差△T，如图5所示，得出最大温差△Tmax和可检测时间段，作为红外热像仪可检测的参考性指标。

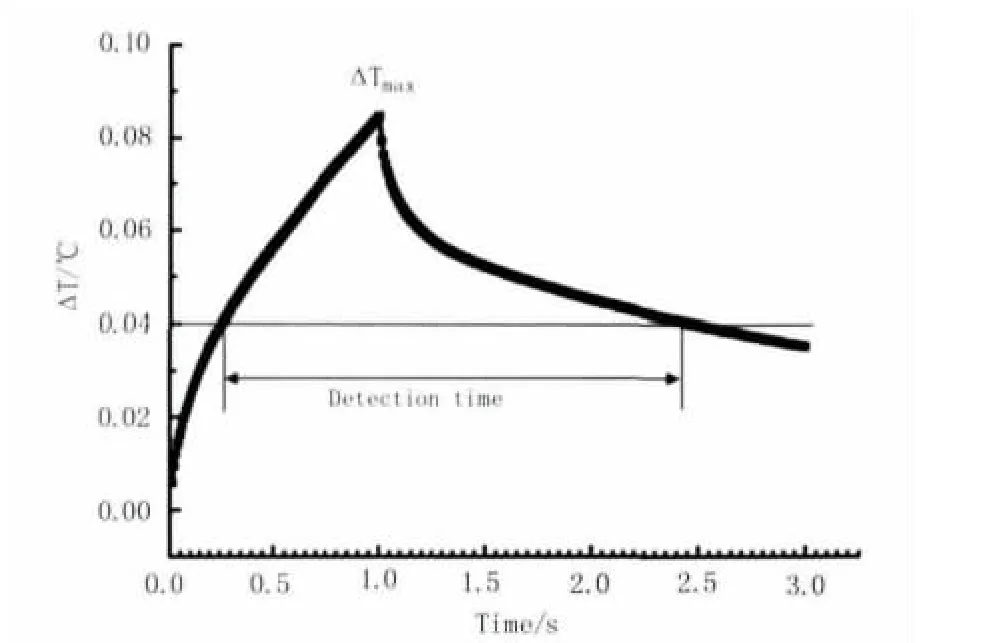
图5 AB两点温度差随时间的变化规律Fig.5 Variation law of temperature difference between two points A and B with time

4 模拟结果与讨论

4.1 埋藏深度对直缝焊管内部裂纹可检测性的影响

内部裂纹离表面距离为埋藏深度，通过对埋藏深度 0.05，0.1，0.2，0.3，0.4 mm 进行对比，从图6和图7可以看出，在焊缝区域，温差分布都是逐渐上升的，到母材区域温差达到平衡，因此参考点B选取在焊缝边缘处;最大温差依次为0.045，0.025，0.02，0.016，0.013℃，埋藏深度为0.05 mm 时，最大温差明显高于其他埋藏深度温差，存在可检测时间0.96 s，其他不存在可检测时间;这是因为在25 kHz的激励频率下，直缝焊管的趋肤深度为0.0565 mm，而电流密度大部分集中趋肤深度以内，因此，当缺陷存在时，其阻碍作用使缺陷处温度升高，并且电流在缺陷上方集聚，从而产生的热源通过热扩散到表面，裂纹上方表面温度也相对更高;但是在趋肤深度以下的裂纹，由于大部分电流在其上方通过，我们认为电流流向并未受到太大影响，所以温差相对较低。

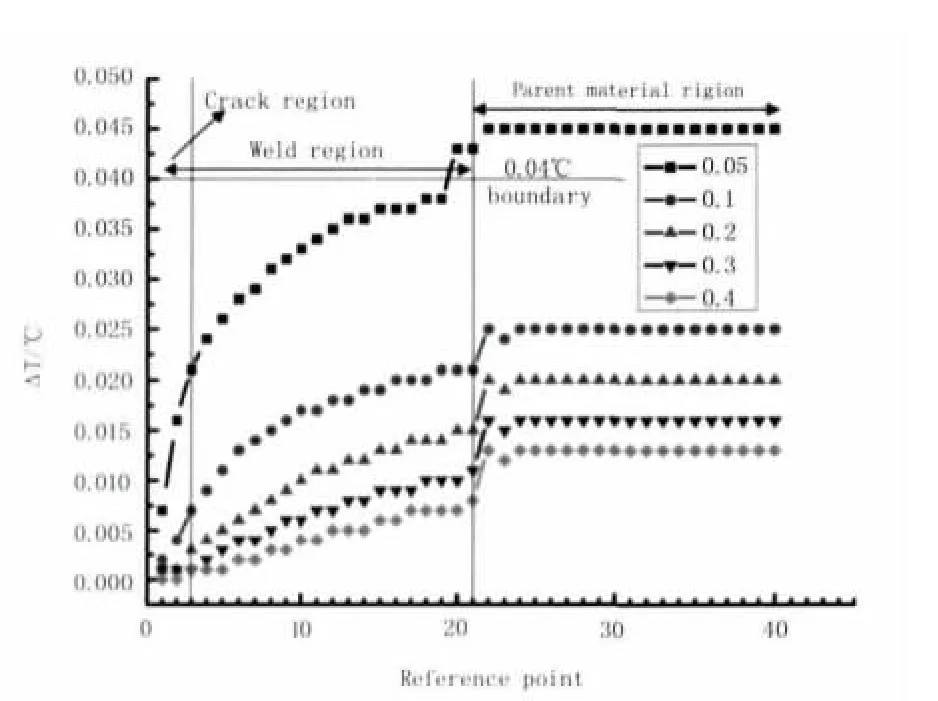
图6 最大温差分布Fig.6 Maximum temperature distribution

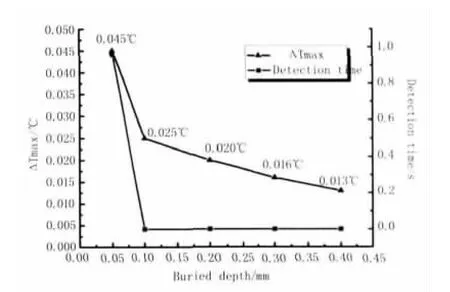
图7 埋藏深度的影响Fig.7 The influence of buried depth

4.2 线圈位置对直缝焊管内部裂纹可检测性的影响

线圈中心离裂纹中心的距离为偏心距离，通过对偏心距离 0，4，8，12，16 mm 进行对比，结果如图 8和图9可见，得到的最大温差依次为0.058，0.056，0.05，0.038，0.023℃(为了更好地作对比，线圈长度由原来的16 mm改为32 mm)，其可检测时间在逐渐下降，当偏心距离为12 mm和16 mm时，不存在可检测时间，这是因为线圈长度的增加，磁感应强度增大，最大温差也相应更大，而裂纹离线圈中心越远，磁感应强度越小，所产生流过缺陷的感应电流也越小，不足以产生足够的热扩散到表面。

4.3 不同材料对直缝焊管内部裂纹可检测性的影响

直缝焊管常用的材质普通碳素钢Q235、优质碳素结构钢20、不锈钢1Cr17，其物理性能如表1所示;实验结果如图10所示，最大温差依次为0.057，0.045，0.013℃，可检测时间分别为 0.98，0.96，0s;这是由于20钢的比热容大于Q235，因此热量相同的情况下，Q235升温更快;并且Q235的趋肤深度大于20钢，因此内部裂纹对电流阻碍作用越明显，产生热也越大;而不锈钢1Cr17相对磁导率很小，因此产生的感应电流越小，产生的热不足以被检测出来。

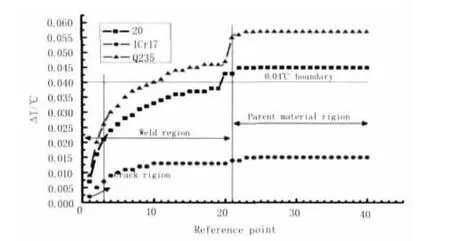
图10 最大温差分布Fig.10 Maximum temperature distribution

4.4 感应加热时间对焊缝内部裂纹可检测性的影响

通过改变激励时间 0.2，0.4，0.6，0.8，1s，如图11和图12所示，其最大温差依次为0.044，0.044，0.044，0.045，0.045℃，但可检测时间呈现直线上升的趋势;这是因为激励时间的增大，直缝焊管的温差保持在一个温度范围不变，当降温的时候才有所下降，因此可检测时间也不断增加。

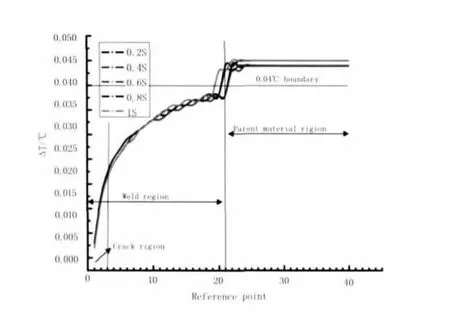
图11 最大温差分布Fig.11 Maximum temperature distribution

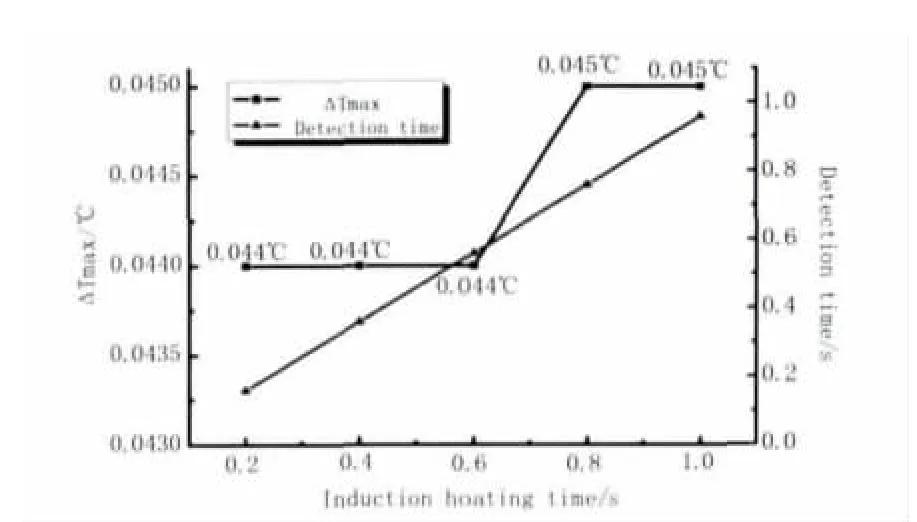
图12 感应加热时间的影响Fig.12 The influence of induction heating time

5 结论

本文通过ANSYS有限元软件对直缝焊管内部裂纹检测模拟仿真，研究分析和模拟计算得出了以下结论:

1)在趋肤深度以内的内部裂纹更加容易能够检测到，对于趋肤深度以下的内部裂纹，可以通过改变激励频率来改变趋肤深度范围或者增大电流强度得到更多的热源，也可以选择更优的红外热像仪，从而达到检测目的。

2)线圈长度的增加，最大温差增大;随着偏心距离的增大，最大温差也逐渐下降，到偏心距离为12 mm时，温差为0.038℃，小于红外热像仪的分辨率，因此内部裂纹无法检测到。

3)铁磁性材料Q235普通碳素钢和20优质碳素结构钢比非铁磁性材料1Cr17不锈钢更容易被检测出来。

4)随着激励时间的增加，最大温差值变化不大，但其可检测时间不断增大。

5)本仿真的结果还有待实践的验证。

［1］ Li Guohua，Wu miao.Modern non-destructive testing ＆ evaluation［M］.Beijing:Chemical Industry Press，2009.(in Chinese)李国华，吴淼.现代无损检测与评价［M］.北京:化学工业出版社，2009.

［2］ Cao Dan，Qu Huiming.Research on material infrared nondestructive testing based on finite element［J］.Laser ＆Infrared，2013，43(5):513 －17.(in Chinese)曹丹，屈惠明.基于有限元的材料红外无损检测研究［J］.激光与红外，2013，43(5):513 －517.

［3］ Wang Chengliang，Yang Bo.Experimental research on ultrasound infrared thermography nondestructive testing for aerial composite materials［J］.Laser ＆ Infrared，2010，40(4):377 －379.(in Chinese)王成亮，杨波.飞机复合材料超声红外无损检测研究［J］.激光与红外，2010，40(4):377 －379.

［4］ Liu Guofei，Li Guohua.Numerical simulation of defect inspection using electromagnetically stimulated thermography［J］.Journal of Shanghai Jiao tong University(Science)，2011，16(3):262 －265.

［5］ N Tsopelas，N J Siakavellas.Electromagnetic-thermal NDT in thin conducting plates［J］.NDT and E International，2008，5(39):391 －399.

［6］ Matej Kranjc，Anze Zupanic.Numerical analysis and thermographic investigation of induction heating［J］.NDT ＆E International，2010(53):3585 － 3591.

［7］ A Risitano，G Risitano.Cumulative damage evaluation of steel using infrared thermography［J］.Theoretical and Applied Fracture Mechanics，2010，54(2):82 －90.

［8］ Liu Junyan，TangQingju，LiuXun，et al.Research on the quantitative analysis of subsurface defects for non-destructive testing by lock-in thermography［J］.NDT and E International，2012，45:104 －110.

［9］ Mengchun Pan，Yunze He.Defect characterisation using pulsed eddy current thermography under transmission mode and NDT applications［J］.NDT and E International，2012，52:28 －36.

［10］ Yang Shiming，Tao Wenquan.Heat transfer［M］.Beijing:Higher Education Press，1998.(in Chinese)杨世铭，陶文铨.传热学［M］.北京:高等教育出版社，1998.