基于谐振环的太赫兹吸波体等效电路研究

周 龙，张文涛，胡放荣，熊显名

(桂林电子科技大学电子工程与自动化学院，广西桂林541004)

1 引言

“超材料”(Metamaterial)是采用微细加工技术制作而成的，具有天然材料所不具备的超常物理性质的人工复合结构或复合材料。微波频段的超材料早在十年前就已经出现［1］，由于其优异的电磁行为，基于超材料的微波吸波体［2－4］是进行电磁隐身［5－6］的重要功能器件。

在太赫兹领域，基于超材料的太赫兹吸波体不仅能够大大提高热效应太赫兹探测器的灵敏度，而且能够进行太赫兹雷达的隐身。另外，“超材料”太赫兹吸波体具有超薄的特点，克服了传统吸波体四分之一工作波长的限制，而且吸收效率提高。因此，“超材料”太赫兹吸波体近年来成了国际同行研究的热点课题之一。2008年美国波士顿大学Hu Tao等人采用表面微加工方法研制出了第一个太赫兹超材料窄带吸波体。随后，极化不敏感［7］、宽入射角［8］，多频［9］、宽带［10］太赫兹超材料吸波体也被研制出来。

在太赫兹超材料吸波体的理论研究方面，目前主要有阻抗匹配理论［2］、传输线理论［11］和多次反射干涉理论［12］。传输线理论的关键是建立合理的等效电路模型来分析谐振吸收峰位置随频率的变化。现有文献在建立吸波体等效电路模型［13－14］时都没有考虑入射太赫兹波的偏振方向，这种理论模型对于偏振敏感的太赫兹吸波体是不能适用的。针对基于开口环谐振器结构的太赫兹吸波体，在考虑太赫兹波偏振方向和分析表面电流的基础上，分别建立了吸波体对横电(TE)模和横磁(TM)模的等效电路模型，并研究了吸波体结构参数对吸收峰位置的影响规律。

2 吸波体结构设计与仿真

吸波体单元结构如图1(a)所示，单元边长L=100μm，各单元从上到下依次为金属开口环谐振器(Split ring resonator，SRR)，中间介质(聚酰亚胺:polyimide)层以及金属(Au)基底。其中，金属(Au)电导率σ =4×107s/m，厚度为0.1 μm;聚酰亚胺的相对介电常数为1.8，损耗角正切tanδ=0.025，厚度为H。开口环谐振器的开口宽度为D，线宽为W，半径为R(圆心点到线宽中心点的距离)。吸波体的吸收率计算公式为A=1－|S11|2－|S21|2，其中S11和S21分别表示反射系数和透射系数。由于金属基底的厚度远大于太赫兹波在金属表面的趋肤深度，电磁波不能透过吸波体，故S21=0，吸收率简写为A=1－|S11|2。根据仿真数据代入公式计算得到的吸收率A随频率变化曲线如图1(b)所示。由图可知，吸波体对横磁(TM)模的吸收峰位置为1.27 THz，而对横电(TE)模的吸收峰位置为1.85 THz。

图1 结构设计与仿真

3 吸波体等效电路模型

表面电荷在入射波电场的作用下发生移动产生表面电流，横磁(TM)模入射所产生的表面电流如图2(a)、(b)所示，横电(TE)模产生的表面电流如图3(a)、(b)所示。通过观察谐振器和金属基底的表面电流分布情况可知，两种模式入射时吸波体的谐振模式是不同的，因此，我们对两种情况分别建立等效电路模型。

首先分析横磁(TM)模入射的情况，由于横磁(TM)模的电场E平行于谐振环开口处上下两个极板，在此模式下谐振器开口没有起到一个电容的作用，不能被等效为一个电容，由横磁(TM)模产生的谐振环(见图2(a))及金属基底(图2(b))的表面电流分布情况可以看出，谐振环上下两个部分的电流是相对独立的，谐振环没有单独形成谐振回路，但是整个吸波体结构却发生了谐振，产生谐振所需的电容源于谐振器与金属基底之间的等效电容［14］，由此得到横磁(TM)模入射所对应的等效电路(见图2(c))。其中，L1、L2、分别为谐振器上、下两个部分的等效电感，C1、C2是谐振器上、下两个部分分别与金属基底形成的等效电容。

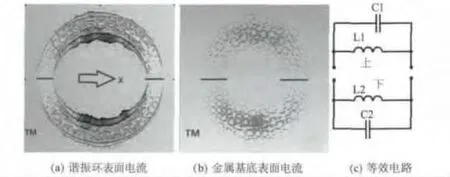
图2 横磁(TM)模入射表面电流的分布情况及其对应的等效电路

由此得到横磁(TM)模对应的吸波体谐振频率:

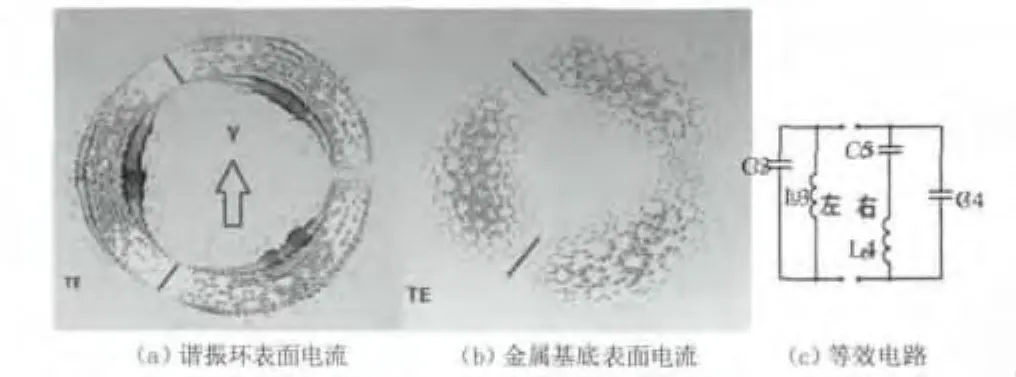
图3 横电(TE)模入射表面电流的分布情况及其对应的等效电路

同理，分析如图3(a)、(b)所示横电(TE)模式对应的表面电流，谐振器左右两个部分与金属基底形成两个相对独立的LC振荡电路，由此得到横电(TE)模入射的等效电路(图3(c))。其中，L3、L4为谐振器左、右两个部分的等效电感，C3、C4为谐振器左、右两部分别与金属基底形成的等效电容。同时由于电场E垂直于谐振环开口处上下两个平行极板，谐振器开口应等效为电容，即C5。尽管左、右两个部分的等效电路结构不同，但是其谐振频率始终保持一致，得到横电(TE)模对应的吸波体谐振频率:

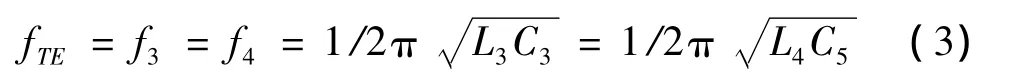
4 等效电路模型的验证

现在根据等效电路模型来研究吸波体结构几何参数D、R、W、H变化对其吸收峰位置的影响规律。当谐振器开口D发生变化时，根据前文的分析，横磁(TM)模入射的等效电路不存在谐振器开口的等效电容，所以不影响其谐振频率。当横电(TE)模入射，D增加，等效电容C5减小，谐振频率fTE增加(见式(3))，如图4(a)。当R增加，谐振器与金属基底的相对面积增加，等效电容 C1、C2、C3、增加，同时等效电感L1、L2、L3、L4也随R的增加而增加，所以横磁(TM)模谐振频率fTM和横电(TE)模谐振频率fTE都减小(见式(1)和式(3))，如图4(b)。当W增加，谐振器与金属基底的相对面积增加，等效电容C1、C2、C3、增加，同时，谐振器开口的相对面积也增加，等效电容C5增加，所以横磁(TM)模谐振频率fTM和横电(TE)模谐振频率fTE都随W的增加而减小(见式(1)和式(3))，如图4(c)。当H增加，谐振器与金属基底之间距离增加，等效电容C1、C2减小，横磁(TM)模谐振频率fTM增加(见式(1))。横电(TE)模入射，式(3)中只有等效电容C3发生变化，谐振频率几乎不会改变，只是由于介质层厚度增加使其吸收率增加，如图4(d)，以上分析结果总结如表1所示。

表1 结构参数(D、R、W、H)对TM和TE模谐振频率的影响

图4 吸波体结构参数对吸收峰的影响

图4(a)～(d)所示的结果与以上理论推导完全一致，说明利用此等效电路模型分析吸波体结构参数对其吸收峰位置的影响规律是完全正确的。

5 总结

本文通过分析横电(TE)模和横磁(TM)模入射时太赫兹超材料吸波体表面电流的分布情况，分别建立了两种入射情况下吸波体的等效电路模型，并利用CST微波分析软件对等效电路模型进行了验证。利用等效电路模型研究了当吸波体结构参数对谐振吸收峰位置的影响规律。这种等效电路模型，为太赫兹吸波体的结构设计和性能研究提供了重要参考。

［1］ D R Smith，W J Padilla，D C Vier，et al.Composite medium with simultaneously negative permeability and permittivity［J］.Phy.Rev.Lett，2000，84(18):4184 －4187.

［2］ N I Landy，S Sajuyigbe，J J Mock，et al.Perfect metamaterial absorber［J］.Phy.Rev.Lett，2008，100(20):207402－207405.

［3］ Weiren Zhu，Xiaopeng Zhao.Metamaterial absorber with random dendritic cells［J］.Eur.Phys.J.Appl.Phys，2010，50(2):21101 －21104.

［4］ Gu Chao，Qu ShaoBo，Pei ZhiBin，et al.Planar metamate-rial absorber based on lumped elements［J］.Chin.Phys.Lett.，2010，27(11):117802 －117804.

［5］ J B Pendry，D Schurig.Controlling electromagnetic field［J］.Science，2006，312(5781):1780 －1782.

［6］ D Schurig，J J Mock，B JJustice .Metamaterical electromagnetic cloak microwave frequencies［J］.Science，2006，314(5801):977－980.

［7］ N I Landy，C M Bingham，T Tyler，et al.Design，theory，and measurement of a polarization-insensitive absorber for terahertz imaging［J］.Phys.Rev.B 2009，79(12):123104－123108.

［8］ Y Q Xu，P H Zhou，H B Zhang，et al.A wide-angle planar metamaterial absorber based on split ring resonator coupling［J］.J.Appl.Phys.，2011，110(4):44102 －44107.

［9］ Wu Xiang，Pei ZhiBin，Qu ShaoBo.Design and experimental verification of band-pass frequency selective surface based on metamaterial effective medium theory［J］.Journal of Infrared and Millimeter Waves，2011，30(5):469－474.

［10］ G D Wang，M H Liu，X W Hu.Broadband and ultra-thin terahertz metamaterial absorber based on multi-circular patches［J］. EurPhyJourB，2013，86(7):30879－30885.

［11］ Q Y Wen，Y S Xie，H W Zhang，et al.Transmission line model and fields analysis of metamaterial absorber in the terahertz band ［J］.Opt.Express，2009，17(20):256－265.

［12］ H T Chen.Interference theory of metamaterial perfect absorbers［J］.Opt.Express，2012，20(7):7165 － 7172.

［13］ M P Hokmabadi，D S Wilbert，P Kung.Design and analysis of perfect terahertz metamaterial absorber by a novel dynamic circuit model［J］.Opt.Express，2013，21(14):16455－16465.

［14］ YU Qian Ye，Yi Jin，Sailing He.Omnidirectional，polarization-insensitive and broadband thin absorber in the terahertz regime［J］.Opt Physics，2010，27(3):498 －504.