外推Gauss－Seidel迭代法的收敛性及其与H－矩阵的关系

薛秋芳，高兴宝，刘晓光

（1.陕西师范大学数学与信息科学学院，西安 710062；2.西安理工大学应用数学系，西安 710054）

外推Gauss－Seidel迭代法的收敛性及其与H－矩阵的关系

薛秋芳1，2，高兴宝1，刘晓光1

（1.陕西师范大学数学与信息科学学院，西安 710062；2.西安理工大学应用数学系，西安 710054）

考虑外推Gauss－Seidel迭代法的收敛性及其与H－矩阵的关系，给出了外推Gauss－Seidel迭代法与Jacobi迭代法收敛性的关系及收敛的参数范围.利用最优尺度矩阵及M－1N的估计量给出了H－矩阵外推Gauss－Seidel法谱半径的上界估计式，并基于外推Gauss－Seidel及Gauss－Seidel迭代法得到一般H－矩阵的等价条件.

H－矩阵；Gauss－Seidel迭代法；外推Gauss－Seidel迭代法；最优尺度矩阵；谱半径

0 引 言

对大型稀疏线性方程组

一般采用迭代法求解，这里：A＝（aij）为n×n阶方阵；x和b均为n维向量.经典的迭代法有Jacobi迭代法、Gauss－Seidel迭代法、SOR迭代法和AOR迭代法等.为改进迭代收敛性，加快迭代收敛速度，对不同的迭代法人们又提出了相应的外推迭代法，如外推Jacobi迭代法和外推Gauss－Seidel迭代法等.本文讨论外推Gauss－Seidel迭代法.

设A＝D－L－U，其中：D，－L和－U分别是A的对角、严格下三角和严格上三角矩阵，则A的Gauss－Seidel迭代法（简称GS迭代法）是基于分裂A＝（D－L）－U得到的，其迭代格式为

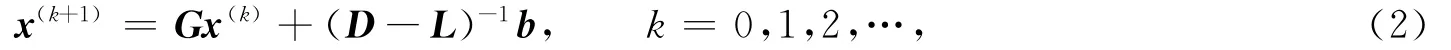
其中G＝（D－L）－1U为Gauss－Seidel迭代矩阵.相应的外推Gauss－Seidel迭代法（简称EGS方法）迭代格式为

其中：G h＝（1－h）I＋h G为外推Gauss－Seidel迭代矩阵；h为外推参数.显然，EGS迭代法是GS迭代法的推广.当h＝1时，其即为GS迭代法.目前，对外推迭代法收敛性的研究已有许多成果［1－11］.文献［1］基于原迭代矩阵T的特征值给出了一般外推迭代法收敛的外推参数范围.

定理1［1］外推迭代法收敛的充分必要条件是下列条件之一成立：

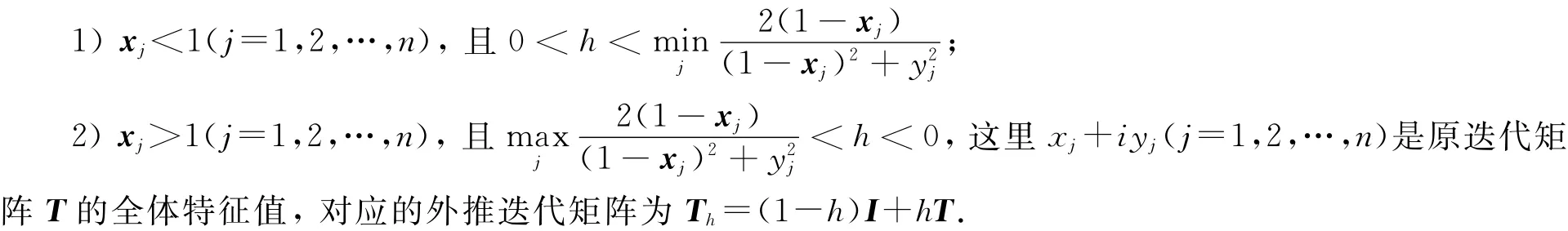
文献［2］基于SSOR迭代法讨论了H－矩阵的等价条件；文献［3］讨论了H－矩阵的块AOR和块SAOR迭代法的收敛性，基于块Jacobi迭代法给出了当参数在一定范围时其谱半径的上界估计式.Bru等［4］基于Jacobi迭代法给出了H－矩阵的如下等价条件：

定理2［4］设A＝（aij）∈Cn×n满足a ii≠0（i＝1，2，…，n），则下列条件等价：

1）A为H－矩阵；

2）对任意的P∈Ω（A），ρ（J（P））＜1.

这里：ρ（J（P））为P的Jacobi迭代矩阵的谱半径；Ω（A）为A的等模矩阵集合.

文献［5］基于EGS迭代法给出了不可约H－矩阵的等价条件：

定理3［5］设A＝（aij）∈Cn×n为不可约方阵，且aii≠0，则下列条件等价：

1）A为H－矩阵；

这里：ρ（｜J｜）为A的Jacobi迭代阵绝对值的谱半径；Ω（A）为A的等模矩阵集合.

本文进一步研究EGS迭代法的收敛性，讨论EGS迭代法收敛性与H－矩阵的关系，从而将文献［4］中基于Jacobi迭代法的H－矩阵等价条件推广为基于EGS迭代法的等价条件，并将文献［5］中关于不可约H－矩阵的等价条件推广到一般的H－矩阵.

1 EGS迭代法的收敛性

引理1［13］设方阵E≥0，F≥0，B＝E＋F，若ρ（E）≤1，则下列结论成立：

1）当ρ（B）＜1时，0≤ρ（（I－E）－1F）≤ρ（B）＜1；

2）当ρ（B）＝1时，ρ（（I－E）－1F）＝ρ（B）＝1；

3）当ρ（B）＞1时，ρ（（I－E）－1F）≥ρ（B）＞1.

由引理1，对L－矩阵，可建立如下EGS迭代矩阵的谱半径与Jacobi迭代矩阵谱半径的关系.

定理4设A是L－矩阵，则下列结论成立：

1）当ρ（J）＜1时，1－h≤ρ（G h）≤（1－h）＋hρ（J）＜1；

2）当ρ（J）＝1时，ρ（G h）＝ρ（J）＝1；

3）当ρ（J）＞1时，ρ（G h）≥（1－h）＋hρ（J）＞1.

这里0＜h≤1.

证明：显然G＝（D－L）－1U＝（I－D－1L）－1D－1U，J＝D－1（L＋U）＝D－1L＋D－1U.令E＝D－1L，F＝D－1U，则G＝（I－E）－1F，J＝E＋F并且ρ（E）＝0.由A为L－矩阵可知E≥0，F≥0，从而由引理1可知：当ρ（J）＜1时，0≤ρ（G）≤ρ（J）＜1；当ρ（J）＝1时，ρ（G）＝ρ（J）＝1；当ρ（J）＞1时，ρ（G）≥ρ（J）＞1.因为G h＝（1－h）I＋h G，0＜h≤1，所以ρ（G h）＝（1－h）＋hρ（G），进而由ρ（G）和ρ（J）的关系可得：当ρ（J）＜1时，1－h≤ρ（G h）≤（1－h）＋hρ（J）＜1；当ρ（J）＝1时，ρ（G h）＝ρ（J）＝1；当ρ（J）＞1时，ρ（G h）≥（1－h）＋hρ（J）＞1.证毕.

由定理4知，当0＜h≤1时，L－矩阵的EGS迭代法是否收敛依赖于Jacobi迭代法是否收敛.

下面讨论复矩阵EGS迭代法的收敛性.

证毕.

定理6表明对一类特殊的复矩阵，当外推参数在一定范围时，不仅可以确定其EGS迭代法收敛，而且可以明确给出其迭代矩阵的谱半径.下面讨论H－矩阵EGS迭代法的收敛性.

2 H－矩阵与EGS迭代法收敛性的关系

推论3若A为M－矩阵，则ρ（G（A））≤ρ（J）＜1，其中J为A的Jacobi迭代阵.

由推论3，当A为M－矩阵时，无论其是否不可约，它的GS迭代法和Jacobi迭代法均收敛，且其GS迭代法收敛速度不慢于Jacobi迭代法收敛速度.

由定理8可将文献［5］中定理1推广到可约H－矩阵的情形.

定理9设A为n阶复方阵，且对任意的i，aii≠0，则下列条件等价：

1）A为H－矩阵；

2）定理9将文献［5］中不可约H－矩阵的等价条件推广到一般的H－矩阵，包括可约H－矩阵和不可约H－矩阵.

3）文献［4］给出了H－矩阵基于Jacobi迭代法收敛性的等价条件（定理2），而本文的定理9则给出了H－矩阵基于EGS迭代法收敛性的等价条件.

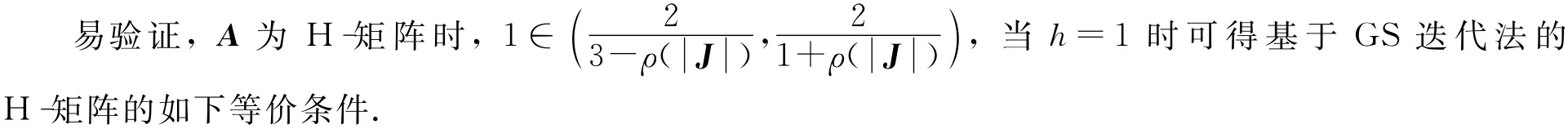
定理10设A＝（aij）∈Cn×n，且aii≠0，则下列条件等价：

1）A为H－矩阵；

2）对任意的P∈Ω（A），ρ（G（P））＜1；

3）〈A〉的GS迭代法收敛，即ρ（G（〈A〉））＜1.

这里G（〈A〉）和G（P）分别为〈A〉和P的Gauss－Seidel迭代阵.

证明：显然1）可以推出2）和3）.反之，如果3）成立，由文献［5］中推论1的证明可知，A是H－矩阵，即1）成立，从而2）成立.所以，当A为H－矩阵时，1）～3）等价.证毕.

类似文献［5］的讨论，对矩阵A定义集合：

3 数值实例

综上，本文研究了外推Gauss－Seidel迭代法的收敛性，讨论了H－矩阵与其EGS迭代法收敛性的关系，得到了EGS迭代法的收敛性结论，并给出了H－矩阵EGS迭代法的收敛范围及其谱半径上界的估计式，从而将文献［5］中的不可约H－矩阵的等价条件推广到一般的H－矩阵，还给出了一般H－矩阵的几个等价条件，进一步发展和完善了H－矩阵的相关理论.

［1］ CAO Zhihao.A Convergence Theorem on an Extrapolated Iterative Method and Its Applications［J］.Applied Numerical Mathematics，1998，27（3）：203－209.

［2］ Alefeld G，Varga R S.Zur Konvergenz des Symmetrischen Relaxationsverfahren［J］.Numerische Mathematik，1976，25（3）：291－295.

［3］ XIANG Shuhuang，ZHANG Shenglei.A Convergence Analysis of Block Accelerated Over－Relaxation Iterative Methods for Weak Block H－Matrices to Partitionπ［J］.Linear Algebra and Its Applications，2006，418（1）：20－32.

［4］ Bru R，Corral C，Gimenez I，et al.Classes of General H－Matrices［J］.Linear Algebra and Its Applications，2008，429（10）：2358－2366.

［5］ 薛秋芳，高兴宝，刘晓光.H－矩阵基于外推Gauss－Seidel迭代法的几个等价条件［J］.山东大学学报：理学版，2013，48（4）：65－71.（XUE Qiufang，GAO Xingbao，LIU Xiaoguang.Several Equivalent Conditions for H－Matrix Based on the Extrapolated Gauss－Seidel Iterative Method［J］.Journal of Shandong University：Natural Science，2013，48（4）：65－71.）

［6］ Evans D J，Martins M M.On the Convergence of the Extrapolated AOR Method［J］.International Journal of Computer Mathematics，1992，43（3／4）：161－171.

［7］ WANG Xinmin，Evans D J.Convergence of the Extrapolated AOR and SOR Iterative Methods［J］.International Journal of Computer Mathematics，1994，52（1／2）：65－74.

［8］ Kohno T，Niki H，Sawami H，et al.An Iterative Test for H－Matrix［J］.Journal of Computational and Applied Mathematics，2000，115（1／2）：349－355.

［9］ 干泰彬，黄廷祝.非奇异H－矩阵的实用充分条件［J］.计算数学，2004，26（1）：109－116.（GAN Taibin，HUANG Tingzhu.Practical Suffcient Conditions for Nonsingular H－Matrices［J］.Mathematica Numerica Sinica，2004，26（1）：109－116.）

［10］ GUO Zhijun，YANG Jianguang.A New Criteria for a Matrix Is Not Generalized Strictly Diagonally Dominant Matrix［J］.Applied Mathematical Sciences，2011，5（6）：273－278.

［11］ 郭丽.非奇异H－矩阵的判定［J］.吉林大学学报：理学版，2010，48（2）：226－228.（GUO Li.Criteria for Nonsingular H－Matrices［J］.Journal of Jilin University：Science Edition，2010，48（2）：226－228.）

［12］ Berman A，Plemmons R J.Nonnegative Matrices in the Mathematica Sciences［M］.New York：Academic Press，1979.

［13］ WANG Xinmin.Generalized Stein－Rosenberg Theorems for the Regular Splittings and Convergence of Some Generalized Iterative Methods［J］.Linear Algebra and Its Applications，1993，184：207－234.

［14］ Young D M.Iterative Solution of Large Linear Systems［M］.New York：Academic Press，1971.

［15］ 胡家赣.尺度变换和矩阵分解的收敛性［J］.计算数学，1983（1）：72－78.（HU Jiagan.Scaling Transformation and Convergence of Splittings of Matrix［J］.Mathematica Numerica Sinica，1983（1）：72－78.）

［16］ HU Jiagan.Upper Bounds of the Spectral Radii of Some Iterative Matrices［J］.Journal of Computational Mathematics，1990，8（2）：118－127.

Convergence of Extrapolated Gauss－Seidel Iterative Method and Its Relationship with H－Matrix

XUE Qiufang1，2，GAO Xingbao1，LIU Xiaoguang1
（1.CollegeofMathematicsandInformationScience，ShaanxiNormalUniversity，Xi’an710062，China；2.DepartmentofAppliedMathematics，Xi’anUniversityofTechnology，Xi’an710054，China）

The convergence performance of the extrapolated Gauss－Seidel iterative method and its relationship with H－matrix were discussed.The convergence relationship between the extrapolated Gauss－Seidel and the Jacobi iterative methods and also the range of the extrapolated parameter when the method converges were given.The upper bound estimates for the spectral radius of the extrapolated Gauss－Seidel iterative method were obtained by using the optimally scaled matrix and the estimator ofM－1N.Meanwhile，equivalent conditions for general H－matrices based on the extrapolated Gauss－Seidel and the Gauss－Seidel iterative methods were provided.

H－matrix；Gauss－Seidel iterative method；extrapolated Gauss－Seidel iterative method；optimally scaled matrix；spectral radius

O241.6

A

1671－5489（2014）03－0413－08

10.13413／j.cnki.jdxblxb.2014.03.03

2013－09－09.

薛秋芳（1978—），女，汉族，博士研究生，讲师，从事数值计算的研究，E－mail：qiufangxue＠163.com.通信作者：高兴宝（1966—），男，汉族，博士，教授，博士生导师，从事智能计算的研究，E－mail：xinbaog＠snnu.edu.cn.

国家自然科学基金（批准号：61273311；10902062）.

赵立芹）