多轴数控专用机床床身动态特性的可靠性优化研究*

展晓珺，蒋立正，2，潘柏松*

(1.浙江工业大学浙江省特种装备制造与先进加工技术重点实验室，浙江杭州310014;2.浙江机电职业技术学院机械工程分院，浙江杭州310053)

0 引言

机床床身的动态特性是影响机床加工精度的重要因素。通过对机床床身动态特性进行可靠性优化，可以在满足床身动态特性可靠度的情况下使床身的重量最小，显著降低制造成本，提高企业的经济效益。

机床床身结构的设计尺寸和布局形式，决定其性能的优劣。目前，国内很多学者研究了筋板布局方式对床身动态性能的影响，通过结果对比选择最佳筋板布局方式，为床身结构优化提供可靠了的依据［1-5］。张祥雷等人［6］对五轴数控磨床床身进行了静、动态特性分析和优化，通过改进床身结构和筋板布置形式提高机床整体刚度。马青芬［7］借助有限单元法，运用灵敏度分析和结构优化的方法，对加工中心床身开展以提高床身的低阶固有频率为目标的动态结构优化设计，得到床身筋板厚度和壁厚的最佳匹配值，床身前两阶固有频率得到提高。耿新海等人［9］对CK2120 六主轴数控车床床身进行了模态分析，并针对分析结果提出了增加外壳板厚和筋板数量的结构改进方法，为合理地避开共振区提供了理论参考。陈叶林等［10］结合基于近似模型的尺寸优化及拓扑优化技术，以床身重量最轻为优化目标，以各板间距和厚度等为设计变量，对床身进行了多目标的优化设计，有效地提高了床身的机械性能。

研究发现，国内对床身动态特性的优化集中在改进筋板结构形式和厚度，忽略了床身的可靠性。为此，本研究综合考虑床身关键尺寸加工误差对床身可靠性的影响，以床身重量最轻为优化目标，以床身动态特性可靠度为约束条件，在满足床身动态特性的基础上对床身进行可靠性优化。

1 多岛遗传算法概述

图1 传统遗传算法和多岛遗传算法相邻两代之间的进化流程图

遗传算法是有鲁棒性的搜索算法，可以解决复杂的大尺度、多变量非线性反演问题。多岛遗传算法(MIGA)继承了传统遗传算法(TGA)的基本思想。两者的区别在于多岛遗传算法将众多种群分成若干个子种群(也被称为岛)，在子种群中执行遗传算法的选择、交叉、变异等操作，并且周期性地在不同岛之间有针对性地进行“迁移”操作，从而保持了优化解的多样性，提高了包含全局最优解的机会。传统遗传算法和多岛遗传算法相邻两代之间的进化流程图如图1所示。

2 多轴数控专用机床床身的模态分析

2.1 床身结构的初步设计

床身采用分体铸造，初步设计为外围长2 150 mm，宽1 375 mm，高1 150 mm，壁厚35 mm;采用高刚性45°斜式管状中空整体结构;床身内部沿导轨方向布置4 个加强筋，导轨两侧分别布置2 个加强筋，可以增强床身的强度和刚性;考虑铸造工艺，加强筋厚度为25 mm。

建立正确有效的有限元模型是进行结构分析和优化改进的基础［11］。床身参数化建模时，不考虑对床身刚度影响不大的小孔、小面、倒角等细小结构，以避免局部生成大量的有限元单元，从而减少工作量。床身结构如图2所示。

图2 床身结构

2.2 床身结构的模态分析

研究模态固有频率可以得到床身的振动情况。主轴最高转速n=3 000 r·min-1，电机产生的转速激励频率fj为:

考虑2 倍的安全裕量，因此床身一阶模态固有频率应该满足:

床身的材料属性如表1所示。床身通过9 个地脚螺栓与地面连接，因此对床身的9 个地脚螺栓孔施加固定约束。本研究采用四面体单元对床身进行网格划分，网格单元长度为20。经提取模态分析的前3 阶固有频率，如表2所示。

表1 床身的材料属性

表2 床身前三阶固有频率

从表2 中可以看出，床身的一阶模态固有频率f为166.25 Hz，大于100 Hz，满足设计要求。

3 基于Isight 集成的床身可靠性优化

可靠性优化设计的目的是在满足可靠性约束的条件下寻求系统的最优解，其将系统不确定性因素定义为随机变量或参量，选择合适的可靠性设计优化策略，建立可靠性优化设计模型，采用合适的优化算法进行优化设计。床身的可靠性优化设计流程图如图3(a)所示。

由于床身优化过程中需要多次迭代，计算量大，而Isight 能够快速集成各种设计和仿真软件，按照指定的优化算法对所集成软件的输入文件进行修改，再调用软件进行求解计算后读取目标函数的值，然后判别目标函数值是否达到最优，如果最优则优化结束，否则对输入文件再次进行修改计算，如此循环直至取得理想的目标函数值，因此，本研究采用Isight 集成的方法对床身进行优化。Pro/E、ANSYS 和Isight 的集成控制流程图如图3(b)所示。

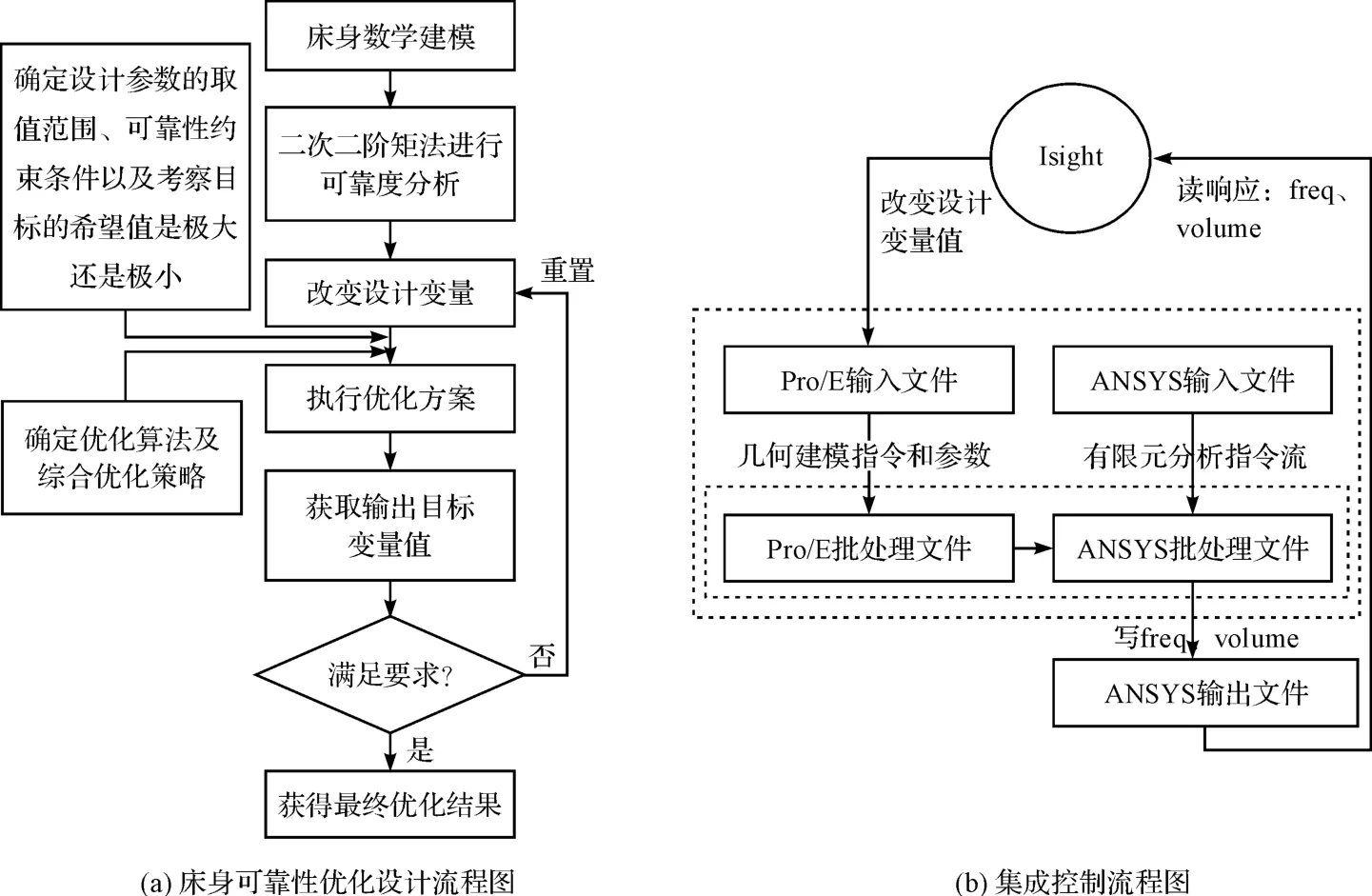
图3 流程图

床身可靠性优化的数学模型表示为:

式中:V—床身体积;t—床身外围壁厚;j—加强筋厚度;n1—副主轴区域加强筋数量(由于对称关系，只取一侧的数量);n2—主轴区域加强筋数量;R—最低可靠度(99.999%);l，u—约束极值的上下标。

床身的参数示意图如图4所示。考虑加工误差的影响，床身壁厚和加强筋厚度值在每一点都会有一定的波动，其值服从正态分布。

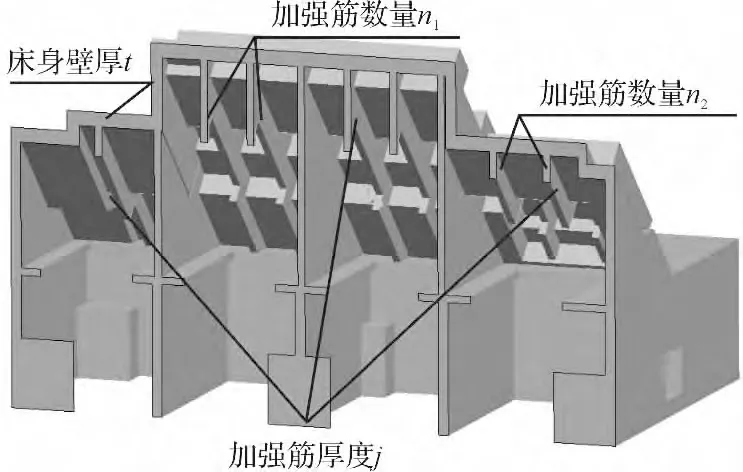
图4 床身关键参数

优化三要素确定后，本研究采用响应面法建立床身的近似数学模型。为了提高模型精度，尽量使采样点均匀，笔者采用DOE 中的拉丁超立方法对设计点进行采样。采样点为110 个，随机取20 个样本点进行误差分析。

设计变量取值范围如下:

4 结果分析

设计变量对一阶固有频率f 影响的输出响应图如图5所示。床身壁厚和加强筋厚度对一阶固有频率的影响如图5(a)所示，可以看出，随着两者的减小，一阶固有频率增大，红色区域为最优解的范围;从图5(b)可以看出，一阶固有频率随加强筋数量的增多而减小;图5(c)中，当加强筋的数量在2～3 之间，加强筋厚度在15～20 之间能取得最优解;图5(d)中，当加强筋数量在2～3 之间，床身壁厚在25～30 之间时能取得最优解。

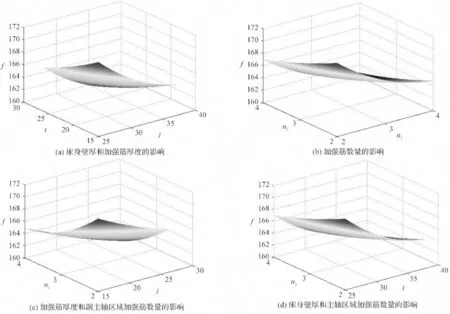
图5 设计变量对一阶固有频率的影响

本研究采用多岛遗传算法对床身进行可靠性优化设计，初始种群数为20，交叉概率为1，变异率为0.01。本研究采用二阶可靠性方法计算优化前后的可靠度。优化结果如表3所示，优化后的床身在一阶模态固有频率基本保持不变的情况下，床身体积(或床身重量)减少了15.23%，可靠度大幅度提高(即失效概率从万分之三降为千万分之一)。

5 结束语

本研究基于Isight 集成仿真对床身动态性能进行了可靠性优化;采用有限元法对床身进行模态分析，求得一阶固有频率。以床身重量最轻为优化目标，基于多岛遗传算法对床身壁厚、加强筋厚度和加强筋数量进行了优化。

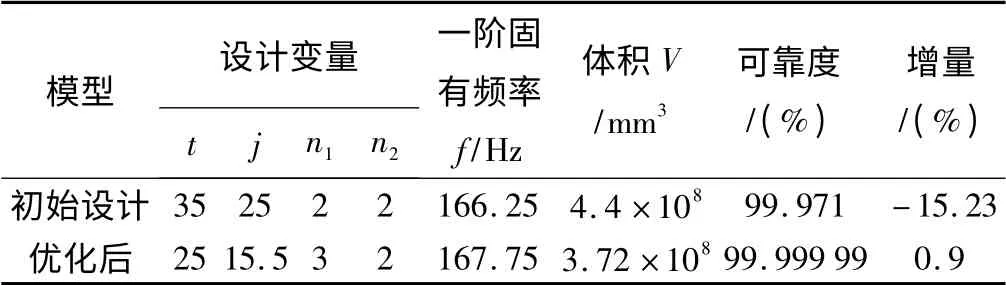
表3 优化结果

优化后床身动态特性的可靠度得到提高，且床身的重量减小了15.23%，达到了节省材料、降低成本的目的，可以为企业带来更大的效益。

［1］倪晓宇，易 红，汤文成，等.机床床身结构的有限元分析与优化［J］.制造技术与机床，2005(2):47-50.

［2］刘 峻.基于ANSYS 的数控冲床床身优化设计［J］.机械研究与应用，2013，26(1):53-55.

［3］陈桂平，文桂林，崔 中.高速磨床床身结构动态分析与优化［J］.制造技术与机床，2009(2):19-23.

［4］杨明亚，王 辉，张长泉，等，数控机床床身筋板布局方式的动态特性分析及优化［J］.贵州大学学报:自然科学版，2013，30(1):37-42.

［5］张士强.锯片对磨机床床身动态分析与优化［J］.组合机床与自动化加工技术，2013(7):34-36.

［6］张祥雷，姚博世，冮铁强，等.五轴数控磨床床身结构分析与优化［J］.机床与液压，2012，40(15):18-21.

［7］马青芬.高速立式加工中心床身结构动态设计［J］.机械制造与研究，2011，40(2):19-21.

［8］耿新海，刘玉堂，王世杰.六主轴数控车床床身的模态分析［J］.装备制造技术，2010(1):71-73.

［9］陈叶林，丁晓红，郭春星，等.机床床身结构优化设计方法［J］.机械设计，2010，27(8):65-68.

［10］WOON S Y，QUERIN O M，STEVEN G P.Structural application of a shape optimization method based on a gentic algorithm［J］.Structural and Multidisciplinary Optimization，2001，22(1):1415-1488.

［11］胡维东，周新建，吴智恒，等.GSLM3308 五轴联动镗铣加工中心立柱有限元分析［J］.机械，2013，40(7):36-39.