限定舒适性的馈能主动悬架系统可回馈能量分析*

陈冬云，杨礼康，*，蔡明龙

(1.浙江工业大学机械工程学院，浙江杭州310014;2.浙江科技学院机械与汽车工程学院，浙江杭州310023)

0 引言

车辆悬架系统在车座舒适性和操纵稳定性方面起着至关重要的作用，特别是主动悬架系统能使车辆获得更好的行驶平顺性。但是主动悬架的高能耗无疑成了这项技术推广的一道障碍。电动式主动馈能悬架概念的提出，为上述问题的解决提出了一种方法，即通过对不平路面引起的振动能量进行回收，将原本以热能形式耗散掉的能量转变为可以利用的电能，以降低主动控制的能耗。

自20世纪70年代末，学者们开始从理论上分析研究车辆悬架的振动能量和回收的可行性。Karnopp［1］揭示了悬架系统的能量耗散过程，指出振动能量回收悬架系统可减低整车驱动功率，对电动车辆尤为有利。Segel［2］分析了悬架系统能量耗散对抑制不平路面振动的影响，计算得到某乘用车在颠簸路面上以13.4 m/s 的速度行驶时，4 个被动阻尼器的能量耗散功率约为200 W。Hsu［3］预测，车辆在高速道路上以96 km/h 车速行驶时，平均每车轮上实际可回收100 W 的振动能量。喻凡、郑雪春［4］理论计算了汽车主动悬架的耗能情况和回收路面振动能量潜能。Abouellnour［5］通过对1/4 悬架建模仿真，估算了某车辆以25 m/s 的车速行驶时，被减振器消耗掉的150 W能量可以转化为电能。Kawaoto［6］设计了主动悬架滚珠丝杠电磁减振器，以20 m/s 的速度在C 级路面上行驶，实验结果表明每个减振器上可以回收15.3 W 能量，主要来自大于2 Hz 的激励频率。

目前，虽有针对馈能式主动悬架的振动能量回收潜力的一些分析和研究，但在仿真分析计算中缺乏一个有效的振动能量计算方法，也没有考虑乘坐舒适性。本研究以此为切入点，建立直线电机式馈能悬架系统模型，对可回收的振动能量进行计算分析，探讨乘坐舒适性与回收能量之间的关系，为进一步合理地匹配直线电机参数，对馈能悬架的设计具有指导意义。

1 直线电机式馈能悬架系统建模

1.1 车辆悬架系统模型

汽车行驶平顺性是指汽车正常行驶时能保证乘客不致因车身振动而引起不舒适和疲乏感觉，以及保持运载货物完整无损的能力。汽车高速行驶在不平路面上，承受具有宽带频谱的振动，频率范围约为0.5 Hz～15 Hz。

为了方便分析被动悬架及主动悬架对车辆行驶动力学(主要指垂直振动)性能的影响及各自能量耗散或需求，本研究假设［7］:①车辆左右两侧完全对称;②车辆前后部分之间相互影响很小;③轮胎的垂向动力学特性可简单地等效为一个忽略阻尼的弹簧，两自由度车辆动力学模型如图1、图2所示。装有被动阻尼器的两自由度1/4 车辆模型如图1所示，由图2 可见，主动悬架采用一个电磁作动器来取代传统被动悬架中的减振器，由于基于电磁作动器的悬架系统是一种阻尼可连续调节的主动悬架系统，是通过调节减振器的阻尼来实现控制的主动悬架系统，此处将电磁作动器模型表示成由机械阻尼cm和电磁阻尼ce(可调)两部分组成。电磁作动器根据控制信号来产生相应大小的作用力，从而实现根据不同工况下的最佳行驶性能，包括乘坐舒适性、车身姿态和轮胎附着性能，同时回收由不平路面激励引起的振动能量。

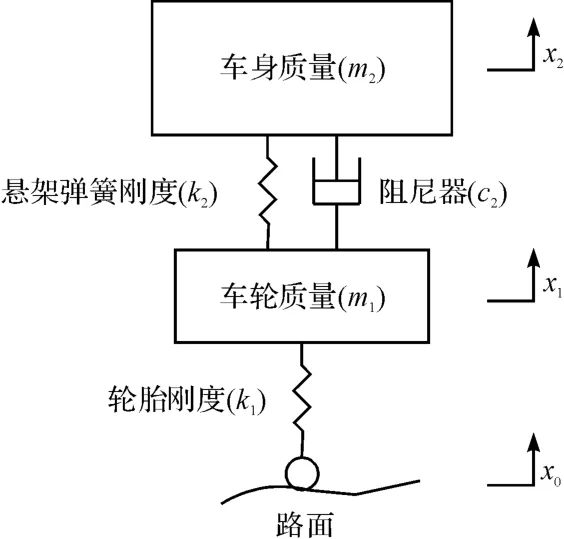
图1 1/4 被动悬架模型

图2 1/4 主动悬架模型

根据牛顿第二定律，可得主动悬架系统的运动方程如下:

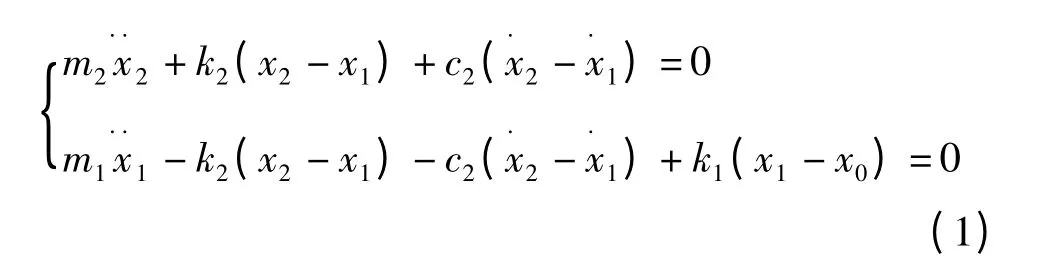
其中，c2=ce+cm，取系统状态向量，输出向量，输入向量U=［x0］。

则其状态方程为:

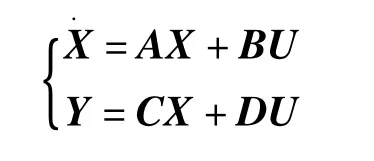
其中:

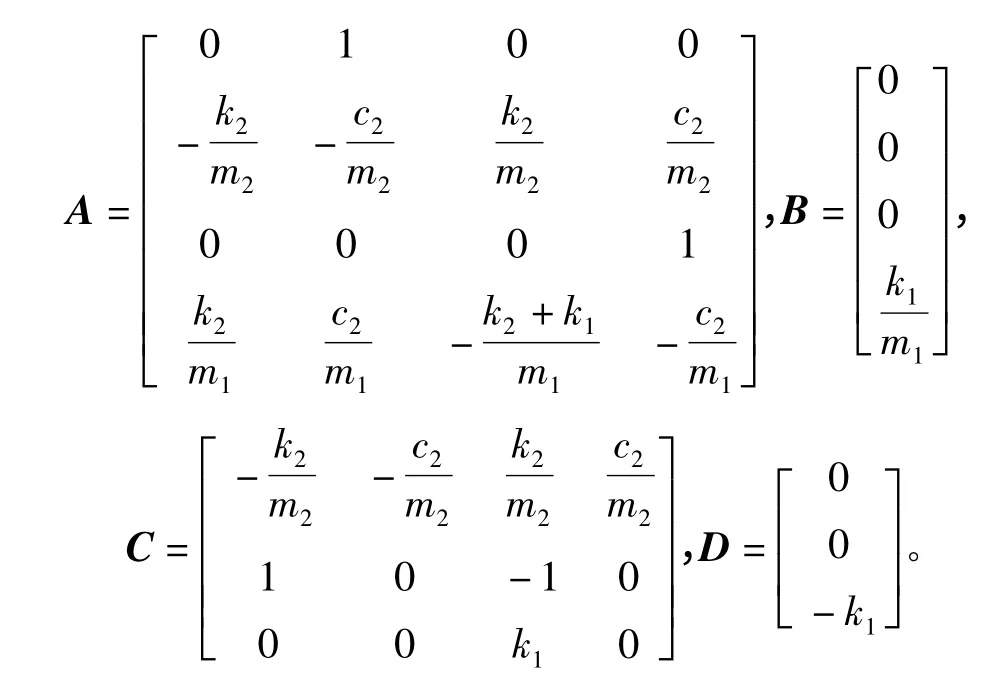
1.2 直线电机式电磁作动器结构

在能量回馈式主动悬架系统中，直线电机被用作动器代替传统被动悬架阻尼器。直线电机是一种将直线运动机械能直接转换成电能或将电能直接转换成直线运动机械能，而不需要任何中间转换机构的传动装置。本研究用直线电机作动器代替传统减振器，在抵消道路冲击的同时回收一部分振动能量。直线电机式馈能作动器结构图如图3所示，其内部装有磁铁和内置线圈［8-9］。

内置线圈通电后可使悬架总成依车身和车轮的相对位置的不同而伸张或收缩。当悬架总成收缩时，直线电机以发电机模式工作，产生作动力。

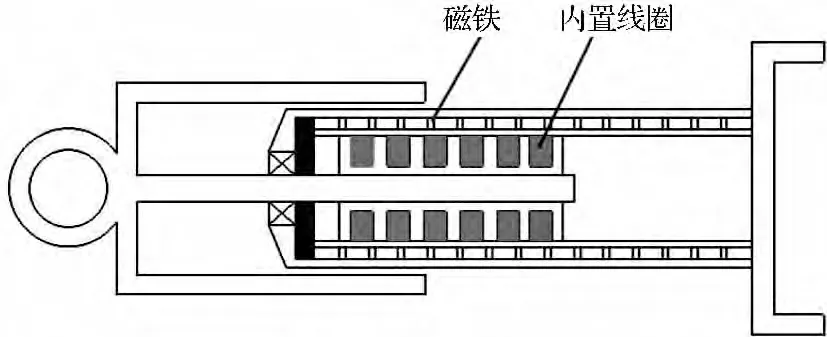
图3 直线电机作动器结构简图

2 直线电机式电磁作动器功率流计算

2.1 电磁作动器功率流

作动器工作时，路面激励引起的振动功率通过馈能悬架系统输入到作动器的功率，一部分被作动器的机械阻尼cm以热能形式耗散，另一部分功率被被直线电机的电磁阻尼ce吸收。被电磁阻尼吸收的这部分功率，一部分被电路内阻以热能的形式耗散，另一部分功率被电路负载电阻吸收，为最终的输出功率，即回收的功率。电磁作动器功率流向示意图如图4所示。

图4 电磁作动器功率流

据此，电磁作动器的功率流可表示为:

式中:P—输入作动器的功率，Pm—机械阻尼耗散的功率，Pe—电磁阻尼吸收的功率，Pa—电路内阻损耗的功率，PL—输出功率(可回收功率)，Ploss—机械阻尼和电路内阻损耗的功率。

2.2 作动器输入的功率计算

在零初始条件下，对式(1)进行拉普拉斯变化并整理得:

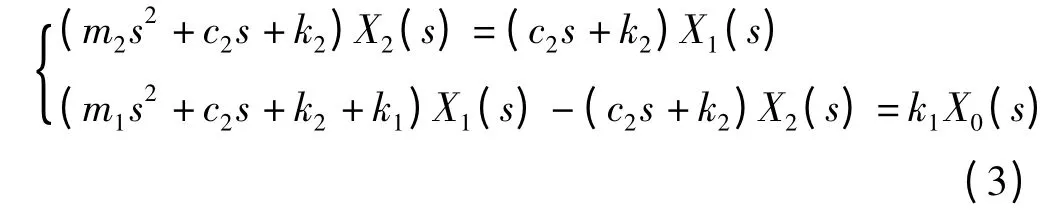
从而可得车身位移、车轮位移和悬架动位移对路面输入的传递函数分别如下式所示:

其中:

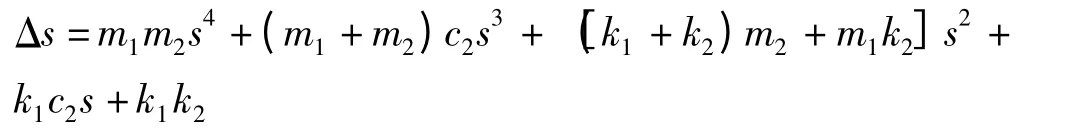
当s=jω 时，悬架动位移(x2-x1)对x0的传递函数为:

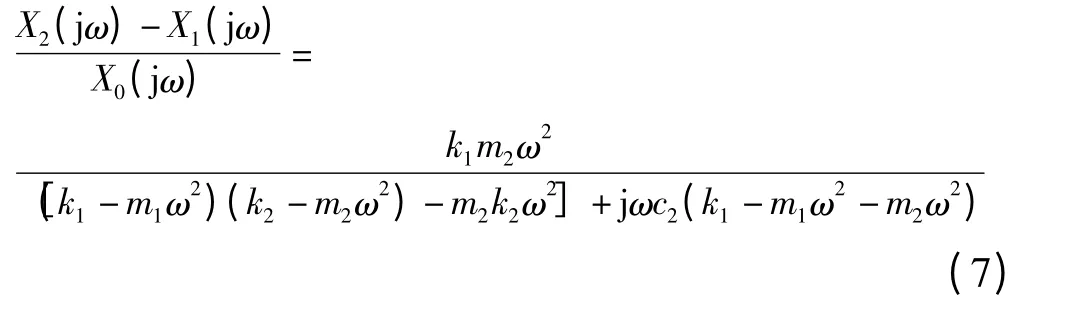
悬架动位移(x2-x1)对x0的幅频特性为:

其中:

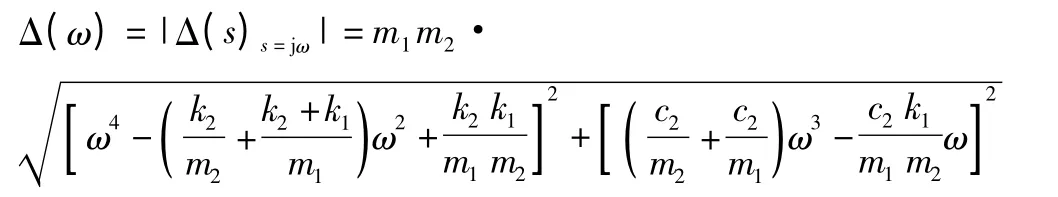
假设悬架动位移z=x2-x1，路面激励为一正弦路面:

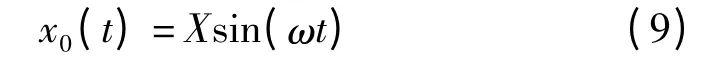
式中:X—激励振幅，ω—激励圆频率或角频率。

对于线性系统而言，若路面激励x0(t)是简谐的，则悬架系统动位移的稳态响应z(t)=x2(t)-x1(t)必定也是简谐的，并且振动频率即等于激振频率ω。

则悬架系统动位移可以表示为:

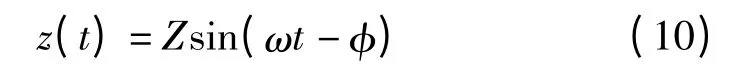
式中:Z—悬架动位移振幅。

可以表示为:

悬架的相对速度为:

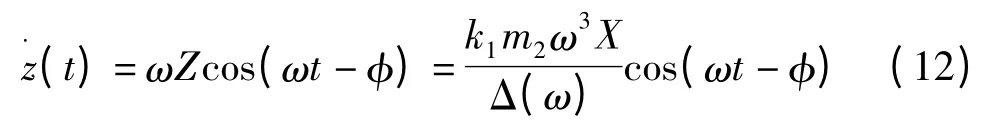
输入减振器的瞬时功率为:

一个周期内输入减振器的能量为:

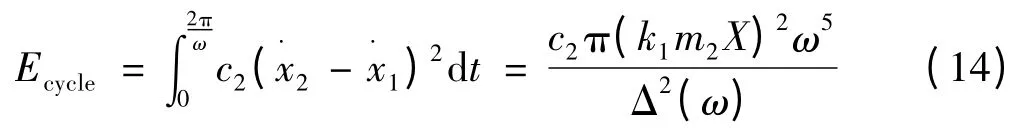
则一个周期内输入减振器的平均功率为:

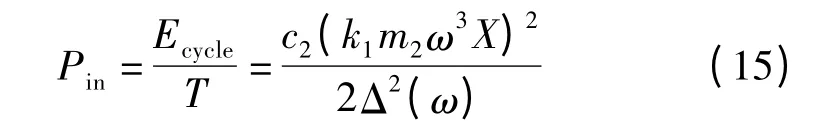
2.3 作动器输出的功率计算

馈能式主动悬架采用直线直流电机作为能量回收装置，其等效电路图简化模型如图5所示［10］。由于汽车悬架系统的振动频率范围很低(0.1 Hz～15 Hz)且直线电机线圈电感值相对较小，电感忽略不计。

在这个模型中，作动器具有如下性质［11］:

(1)电磁阻尼产生的主动作动力F 与电路电流的大小i 成正比:

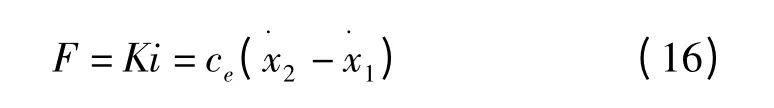
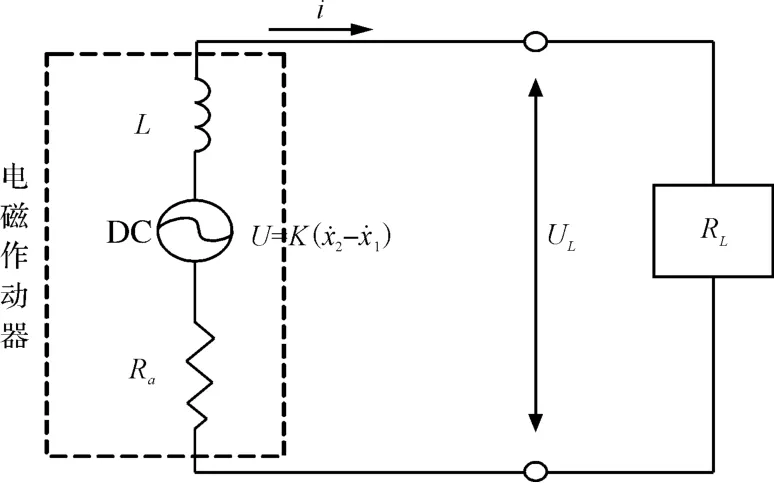
图5 等效电路简化模型

根据基尔霍夫电压定律:

将式(18)代入式(16)，可得电磁阻尼系数为:

将式(12)代入式(18)，可得电枢回路电流为:

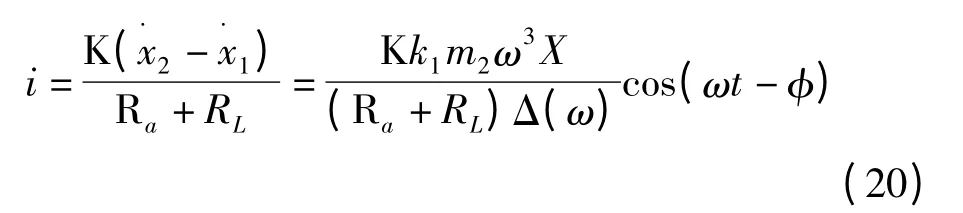
且:

K=NBl

式中:K—直线电机电动势常数，N—线圈绕组匝数，B—平均气隙磁密度，l—线圈绕组总长度，Ra—电枢回路内阻，RL—负载电阻，UL—负载两端的电压。

因为K 和Ra均为一常数，通过调节负载电阻RL的值可以改变电磁阻尼系数ce的大小。

则直线直流电机可回收的瞬时功率为:

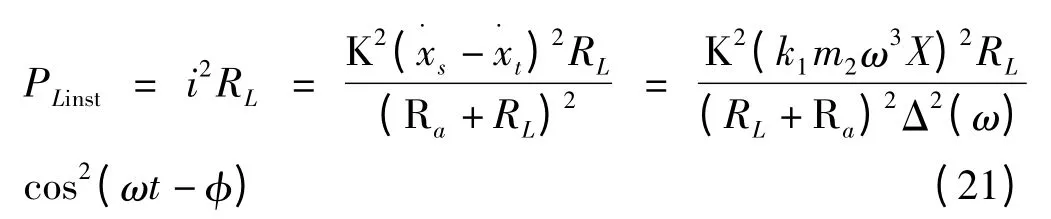
一个周期内直线直流电机可回收的能量为:

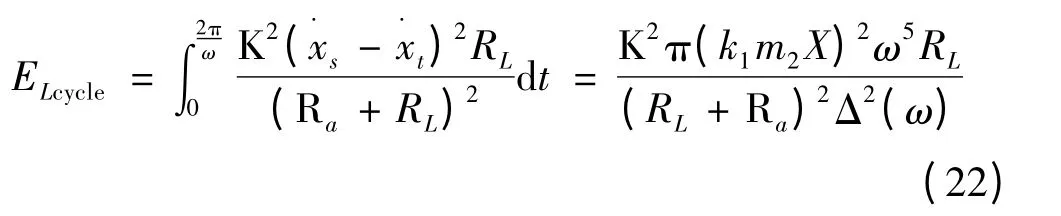
一个周期内直线直流电机平均可回收的功率为:

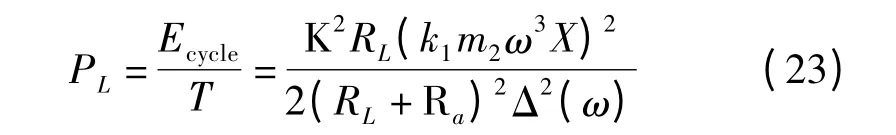
2.4 馈能效率的计算

机械阻尼耗散的功率为:

负载电阻上的瞬时输出功率为:

当dPL/dUL=0 时，即UL=U/2，Ra=RL，负载电阻最大输出功率为:

直线电机式馈能悬架的馈能效率为:

其中:

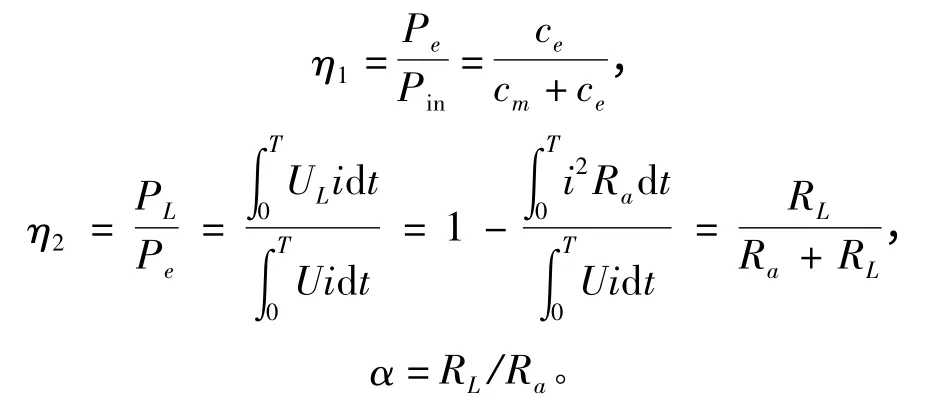
当dη/da=0 时，即达到最大转换效率η⇒ηmax，此时:

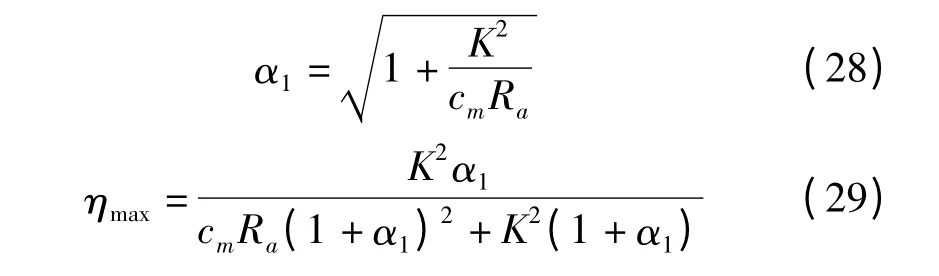
3 仿真计算与实例分析

本研究参照某车型的悬架系统，具体参数如表1所示。直线直流电机参数如表2所示。

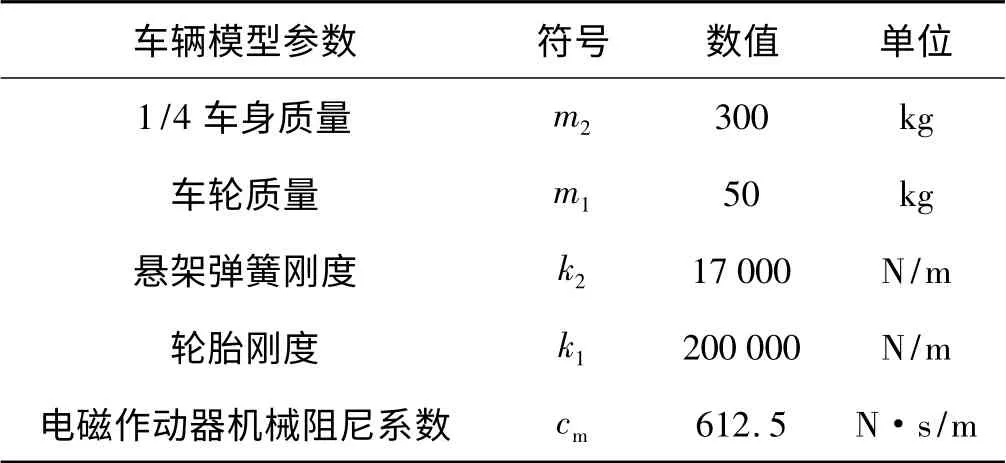
表1 车辆单轮模型参数

表2 直线电机参数

由式(26)可知，当直线电机式馈能悬架的输出功率PL最大时，PL=Pa=4 Ω;由式(28)可知，当直线电机式馈能悬架的馈能效率η 最大时，α1＞1。电磁作动器功率Pin，Pe，PL、效率η1，η2，η 随α 参数的变化曲线图如图6、图7所示。本研究选取最大输出功率对应的外接负载电阻值，即α=1，RL=4 Ω。由式(19)可知ce=612.5 N·s/m，则总阻尼c2=ce+cm=1 225 N·s/m。

假设正弦路面激励振幅为20 mm，激励圆频率ω=1～100。根据式(15，23)利用Matlab 编程进行仿真。输入作动器的功率和回收的功率随激励圆频率的变化曲线分别如图8、图9所示。

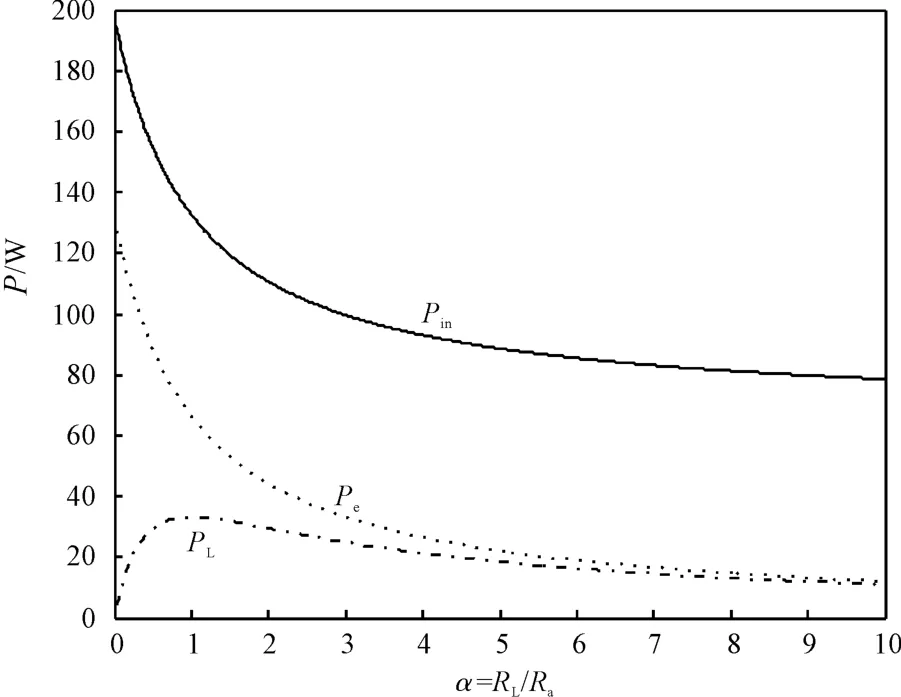
图6 作动器功率流变化曲线图(正弦路面激励振幅X=20 mm，圆频率ω=20)

图7 作动器效率变化曲线图(正弦路面激励振幅X=20 mm，圆频率ω=20)

图8 作动器输入功率曲线图

由图8 可以看出，当车辆行驶在正弦路面上时，减振器存在大量可回收的能量，当激振圆频率ω 在车身、车轮的固有圆频率时，输入减振器的平均功率达到极大值。由图9 可以看出，装有直线直流电机的电磁作动器能够将其中一部分能量进行回收利用，馈能效率达到25%。本研究为探讨车身舒适性与可回收能量之间的关系，为此有选择地选取靠近车身、车轮固有圆频率的6 个正弦路面激励条件，参数如表3所示。

图9 作动器输出功率曲线图

表3 正弦路面激励条件参数

其Matlab/Simulink 仿真模型如图10所示.仿真计算结果如表4所示。

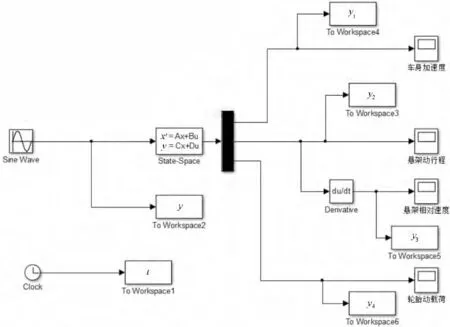
图10 Simulink 仿真模型

分析可见，在正弦路面激励振幅相同的情况下，激励频率越靠近车身、车轮固有频率，车身加速度均方根值越大，对应的乘坐舒适性越低，输入作动器的能量越大，回收的能量也越大。当激励频率在车轮固有频率附近时，车身加速度均方根值很大，乘坐舒适性比较低，同时回收的能量达到1 000 W 以上，直线电机能量回收效率为25%。把作动器的功率流、能量回收的效率与代表乘坐舒适性的车身加速度均方根值联系起来，在满足一定舒适性的前提下，尽可能地回收能量，提高馈能效率。

表4 车身加速度均方根值与回收的能量

4 结束语

本研究通过建立馈能主动悬架系统和直线电机电路模型，结合悬架相对速度对路面激励的幅频特性函数计算出输入作动器的功率以及直线电机回收的功率，然后利用Matlab 仿真软件进行建模仿真。仿真计算结果表明，当车辆行驶在正弦路面上时，路面激励频率与车身加速度、输入作动器的能量、直线电机回收的能量存在一个对应的关系。路面激励越大，馈能悬架的输出功率也越大，既由振动机械能转化成的电能也越多。但是，这是以牺牲车辆的行驶平顺性为代价的，因为路面变差，随动状态(不提供主动力)下的馈能悬架的减振性能也会变差。这往往很难协调，但是如果将主动控制的控制逻辑加入到馈能悬架的控制算法中，使馈能悬架的随动状态与主动控制协调工作，使其具有主动悬架的性能，又能够回收能量，那么馈能悬架就具有得天独厚的优势。因此，通过仿真计算可以针对具体车辆模型参数，设计合理的直线电机参数，以平衡乘坐舒适性和回收能量之间的关系，对馈能式悬架的设计具有一定的参考依据。

［1］KARNOPP D.Power requirement for vehicle suspension systems［J］.Vehicle System Dynamics，1992，21(1):65-71.

［2］SEGEL L，LU X P.Vehicular resistance to motion as influenced by road roughness and highway alignment［J］.Australian Road Research，1982，12(4):211-222.

［3］HSU P.Power Recovery Property of Electrical Active Suspension Systems［C］//Proceedings of the Intersociety Energy Conversion Engineering Conference，Washington，DC，USA，IEEE，1996:1899-1904.

［4］喻 凡，郑雪春.馈能式电动主动悬架的理论及试验研究［D］.上海:上海交通大学机械与动力工程学院，2007.

［5］ABOUELNOUR A，HAMMAD N.Electric Utilization of Vehicle Damper Dissipated Energy［C］.Electronics Research Institute，AEIC，2003.

［6］KAWAMOTO Y，SUDA Y，HOUE H，et al.Modeling of electromagnetic damper for automobile suspension［J］.Journal of System Design and Dynamics，2007，1(3):524-535.

［7］喻 凡，林 逸.汽车系统动力学［M］.北京:机械工业出版社，2005.

［8］陈少君.能量可再生汽车悬架系统建模与控制研究［D］.西安:西北工业大学机械学院，2007.

［9］彭庆红，杜群贵.电动客车变频热泵空调系统及其性能的试验研究［J］.流体机械，2013，41(12):65-69.

［10］ZHU Song-ye，SHEN Wen-ai.Linear electronmagnetic device for vibration damping and energy harvesting:modeling and testing［J］.Engineering Structure，2012(34):198-212.

［11］STEPHEN N G.On energy harvesting from ambient vibration［J］.Journal of Sound and Vibration，2006(93):409-425.