一种新型的单相数字锁相环

张 琪，邱亮明，程善美

（华中科技大学 自动化学院，湖北 武汉 430074）

光伏并网逆变器、UPS电源、PWM整流器等电力电子装置性能很大程度上依赖于锁相环（PLL）对电网电压频率和相位的跟踪能力[1]。目前PLL已有多种实现方法，大致上可以分为两类：周期调节锁相和瞬时调节锁相[2]。周期调节锁相又叫过零锁相，当输入信号干扰较大，存在多个过零点时可能会导致锁相失败。瞬时调节锁相调节速度慢，但是锁相角度误差冲击小，即使存在多个过零点时也能准确锁相，所以目前瞬时调节锁相应用范围广。近年提出的利用离散傅里叶（DFT）变换来提取输入信号基波，即使包含丰富的谐波信号也能准确得到输入信号的基波频率和相位信息。但是当输入信号频率发生波动时，如果采样窗口周期与信号频率比值不能保持恒定，则计算结果会有相位差[3-4]，并且DFT蝶形运算离散化实现时会消耗较多硬件资源。

1 改进的鉴相器(PD)环节

锁相环一般包含鉴相器（PD）、环路滤波器（LF）和压控振荡器（VCO）3个部分[5]。不同锁相环之间的区别大多表现在PD环节[6]。大多数单相锁相环PD环节实现方法主要是基于虚拟坐标变换，需要产生一个与输入信号相差90度的正交信号。产生正交信号的方法有很多，可以根据输入信号频率延时，目前采用较多的是利用两个一阶通用积分器的方法来产生正交信号[7]。文中提出以一个改进的PD环节代替常用的二阶通用积分器构成的PD环节，对于二阶通用积分器，第一个积分环节的累积误差会作为第二个积分环节的输入，从而引起更大的角度误差。数字化实现时，一个积分环节会引起一拍的控制延时，以10K采样频率计算，一拍滞后会引起100 μs的控制延时。对于锁相环而言，这种控制延时是不可忽略的。并且，积分环节会消耗较多的硬件资源。所以相对于常用的二阶通用积分器而言，本文所采用的PD环节误差小，控制延时小，消耗的硬件资源少。其结构如图1所示。

图1 改进的PD环节Fig.1 Improved PD

图1 所示改进的PD环节传递函数为：

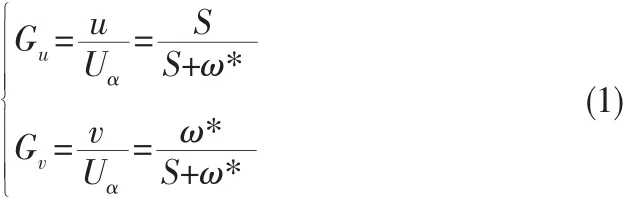
式 （1） 中，ω*为输入信号中心频率。UβUα=Gv-Gu的Bode图如图2所示。如图2所示，输出信号Uβ相对于输入信号Uα在中心频率 ω*（假设为 50 Hz）处滞后 90°，因此输出信号Uβ相对于输入信号Uα在中心频率ω*处是正交的。幅值增益在全频率范围内为1。

图2 改进的PD环节Bode图Fig．2 Bode diagram of improved PD

2 谐波分析

当采用图1所示PD环节时，由图2中幅频响应可以看出，当ω*与参考信号Uα的频率完全相等时，输出信号Uβ相对于输入信号Uα滞后90°，但是在非理想情况下，Uβ相对于输入信号Uα的相移并不为90°。为分析非理想情况下的相移，假设θ很小，那么：

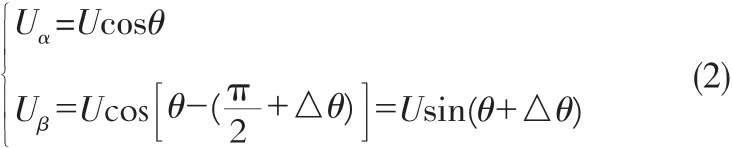
将Uα和Uβ变换变换到dq坐标系，由2s 2r变换公式得

式（3）中θ*为锁相环得到的输入信号相角，此处为便于分析，令 θ*=θ，那么由式（3）可得：

结合式（2）可得：

由式（6）可知，Uα、Uβ经坐标变换之后得到的 Ud分量不仅包含直流量，还包含二次谐波分量，可见，在Uβ相对于Uα在非理想情况下的相移不为准确的90°的情况下，微小的相角偏差会在锁相所得的内部参考信号频率上引起二次谐波扰动，从而导致锁相角度偏差。锁相环一般用于市电电压锁相，其频率一般在中心频率附近微小波动，因此可以用一个带阻滤波器（BSF）滤除锁相所得参考信号频率上的二次谐波扰动。假设以市电作为输入信号，其中心频率为50 Hz，波动范围为±1 Hz。100 Hz为阻带中心频率，3 dB带宽阻带频率范围为95～105 Hz，采样频率为10 kHz，以此参数按双线性变换设计得到的离散化二阶数字带阻滤波器的传递函数为：

其Bode图如图3所示。由图3可以看出，此带阻滤波器对频率为95～105 Hz的信号具有很强的抑制作用，所设计的10 Hz陷波带宽足以应对输入电压的频率波动情况。

图3 带阻滤波器Bode图Fig．3 Bode diagram of band－stop filter

3 基于改进的一阶积分器的仿真分析

基于改进的PD环节的锁相环控制结构框图如图4所示。

图4 基于改进的PD环节锁相环控制框图Fig．4 PLL schematic diagram based on improved PD

按照图4所示控制结构在MATLAB/SIMULINK环境下搭建仿真模型，仿真结果如图 5 所示。 图 5(a)、(b)、(c)、(d)分别给出了输入信号为50 Hz稳态下的输入信号和同步信号波形、输入信号为50 Hz稳态下的输入信号和同步信号相角误差、输入信号频率从50 Hz跳变为60 Hz同步信号与输入信号相位误差及输入信号含有3、5次谐波及白噪声的输入信号和同步信号波形。

由图5可以看出：

1)当输入信号频率稳定为50 Hz时，如图5(a)所示，同步信号在经过2～3个周期之后快速跟踪输入信号，锁相速度快。如图5(b)所示，在输入信号为50 Hz稳定工作情况下，输入信号和同步信号相角误差为0，锁相精度高。

2)如图5(c)所示，输入信号频率从50 Hz跳变为60 Hz同步信号与输入信号相位误差冲击小，过渡过程平缓。电网电压频率波动范围±1 Hz，所设计锁相环足以应对电网频率波动。

3)如图5(d)所示，输入信号受到较大干扰，含有3、5次谐波及白噪声，存在多个过零点的情况下，同步信号能准确跟踪输入信号，抗干扰能力强。

图5 基于改进的PD环节锁相环仿真结果Fig.5 Simulation results based on improved PD loop

4 锁相环实现及物理实验验证

物理实验在80 kVA电力机车辅助变流器系统中单相PWM整流器上完成。锁相环数字化实现在ALTERA公司的EP1C20 FPGA内实现，FPGA控制AD7606获得16位数字信号，锁相环控制结构和模块化均与仿真方案保持一致，基于FPGA的实现顶层框图如图6所示。FPGA内部存储2048点1/4周期正弦信号作为内部基准正余弦信号源，采样频率为10 kHz。

图6 锁相环的FPGA实现框图Fig.6 Schematic diagram of PLL realization based on FPGA

图7 为静态时和辅助变流器工作时的锁相波形。由图7可以看出，静态时锁相方波信号与输入信号在过零点处一致性很好，锁相精度较高[8]。当输入信号受到较大干扰时，锁相环仍能准确跟踪输入信号，稳定可靠工作。

图7 锁相环实验波形Fig.7 Experimental waveforms of PLL

5 结论

文中主要针对常用锁相环PD环节进行研究，用一个改进结构PD环节代替常用的两个一阶通用积分器构成的PD环节，并对其进行分析，优化了控制效果，研究了其基于FPGA的数字实现方法。该方法锁相精度高，速度快，结构简单，计算量较小，工程化实现简单。仿真和实验验证了该锁相环的可靠性和准确性。

[1]Teodorescu R,Blaabjerg F,Liserre M,et al.Proportional resonant controllers and filters for grid-connected voltage-source converters[J].IEE Proceedings on Electric Power Applications,2006,153(5):750-762.

[2]Rubens M,Filho S，Paulo F Seixas.Comparison of Three Single-Phase PLL Algorithms for UPS Applications[J].IEEE Trans.on Industrial Electronics，2008，55(8):2923-2932.

[3]赵文才，范声芳，熊健，等.基于DFT算法的单相数字锁相环[J].电力电子技术，2011,45(4)：79-81.ZHAO Wen-cai,FAN Sheng-fang,XIONG Jian,et al.Single-phase digital phase-locked loop based on DFT[J].Power Electronics,2011,45(4):79-81.

[4]McGrath BP,Holmes D G,Galloway J J H.Power converter line synchronization using a discrete Fourier transform(DFT)based on a variable sample rate[J].IEEE Trans.on Power Electronics,2005,20(4):877–884.

[5]Thacker T,Boroyevich D,Burgos R,et al.Phase-locked loop noise reduction via phase detector implementation for single phase systems[J].IEEE Trans.on Industrial Electronics,2011,58(6):2482–2490.

[6]Golestan S,Monfared M，Francisco D,Freijedo，et al.Dynamics assessment of advanced single-phase PLL structures[J].IEEE Trans.on Industrial Electronics，2013，60(6):2167-2177.

[7]Ciobotaru M,Teodorescu R,Blaabjerg F.A new single-phase PLL structure based on second order generalized integrator[C]//.Proc.37th IEEE PESC.Denmark,2006:1511-1516.

[8]李正兵，蒋兴加，王小丽.高精度新型调制变送器设计与应用[J].火箭推进，2011（5）：69-73.LI Zheng-bing,JIANG Xing-jia,WANG Xiao-li.Design and application of new type high-accuracy modulation transmitter[J].Journal of Rocket Propulsion,2011（5）：69-73.