RLV 末端能量管理段轨迹优化与纵向控制律设计

王 鹏，党晓康，马松辉

（西北工业大学 无人机特种技术重点实验室，陕西 西安710065）

自从第一代可重复使用运载器 （Reusable Launched Vehicle，RLV）出现后，各国对RLV的研究试验从未停止过。其中，以X-33、X-34等验证机为平台，美国在制导与控制技术方面取得了一定的成果[1-3]。末端能量管理段[4-5]为可重复使用运载器所特有，主要是为了耗散飞行器在再入段结束之后所具有的多余的能量，使其在满足各种约束的情况下精确进入自动着陆窗口。RLV在经历末端能量管理段时，很短的时间内从高高度、大马赫数过渡到低高度、亚音速，飞行状态变化剧烈，为了满足自动着陆窗口的位置约束和动压约束，TAEM段需要轨迹规划并跟踪规划轨迹。所以，如何设计一条物理可飞的下滑轨迹并对其进行跟踪是TAEM段的关键。

1 轨迹规划数学描述

TAEM段的目的是消耗和控制能量，RLV的能量包括动能和势能[4]：

其中，m—RLV质量，V—空速，H—RLV高度。

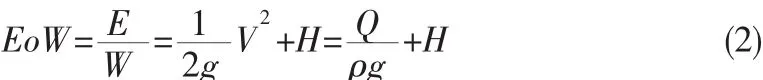
其中，ρ—空气密度。

由上式可以看出，RLV的能量跟H和V密切相关。轨迹的运动属于质点运动范畴。

基于时间历程的质点动力学方程如下所示[4-5]：

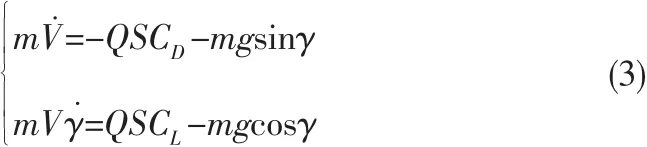
其中，S—RLV参考面积，—航迹倾斜角，CL—升力系数，CD—阻力系数，CL和CD都是迎角、马赫数和控制舵面的函数。

受结构强度限制，RLV飞行过程中需要考虑动压约束，动压同时跟高度和速度相关，而且相对于空速变化缓慢，采用动压代替空速将大大简化轨迹仿真过程。

基于动压的质点动力学方程如下[5]：

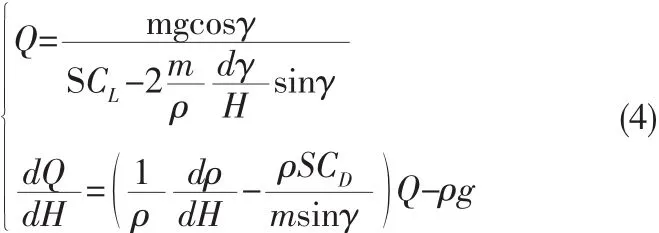
这就将轨迹仿真过程转化为一个优化的过程，寻求合适的迎角、下滑角使得每个高度处的动压和动压变化率满足要求。

直接利用式（4）即可进行离线轨迹设计，为了使质点动力学方程更适应在线轨迹设计，进一步将对高度的微分转化为对待飞距离的微分。

下滑高度、航迹倾斜角和待飞距离之间满足如下关系：

则可得轨迹剖面关于待飞距离的描述[5]：

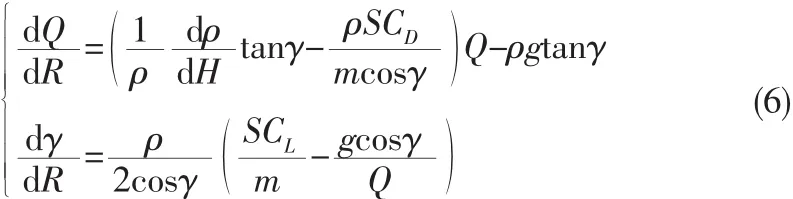
待飞距离定义为沿地轨迹飞行时剩余的飞行距离，待飞距离可以根据地轨迹的几何形状直接计算。

2 轨迹剖面规划

2.1 轨迹规划问题描述

RLV沿轨迹剖面飞行时做拟平衡[5-6]下滑飞行，在下滑过程中，飞行器持续减速，因此速度方向的切向力不平衡，而法向力则处于瞬时平衡状态，则下滑过程中：

则轨迹规划即对于任意给定的高度、速度、航迹倾斜角，寻找满足上述条件的迎角和配平舵面使得RLV满足拟平衡条件。在拟平衡状态下，飞机的航迹倾斜角保持不变，法向力为0，而切向力不为0。

RLV的飞行包线、强度限制等决定了飞行过程中需要对对动压、过载、迎角以及升阻比等加以约束。这样，我们就可以将轨迹的设计问题转化为已知初始状态和终端状态且满足约束条件的优化问题。由于RLV在TAEM段的能量只与高度和速度有关，轨迹设计时可不考虑横侧向机动，将三维轨迹剖面简化为二维轨迹剖面进行设计。

2.2 参数计算

给定某一动压剖面。已知：初始高度H0和初始动压Q0可求得初始马赫数。

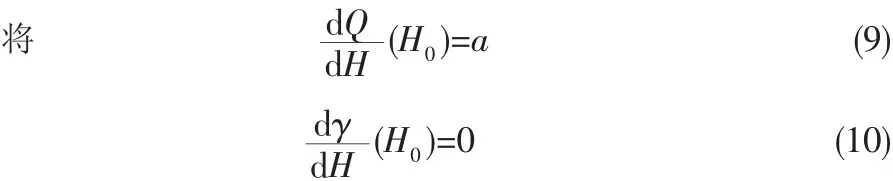
再加上力矩平衡方程可求迎角、轨迹角和配平升降舵。该方程是一个非线性方程，求解方法就是采用优化技术使如下优化指标最小：

固定动压剖面的轨迹仿真[5]，在任意高度上都满足如下条件：

根据第 k 步的 α(Hk)，γ(Hk)，EoW(Hk)，计算 k+1 步的α(Hk+1)，γ(Hk+1)，EoW(Hk+1)，使得性能指标：

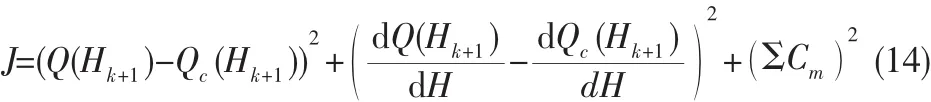
最小。其中，Hk+1=Hk+△H，△H为高度迭代计算步长。

3 标称轨迹跟踪策略

3.1 能量走廊剖面规划

能量走廊[4-5]之内的的任一动压剖面都能产生一个合理（物理可飞）的高度剖面。RLV在实际飞行时不可能沿着一个非线性很强的剖面形状，所以轨迹设计时线性剖面、二次曲线和三次曲线等均可以作为轨迹剖面的形状[5]，在此我们采用线性动压剖面。

由于自动着陆窗口给出了终端约束，即RLV在规划具体的能量走廊时TAEM段初始动压和结束动压已知，能量走廊的最陡下滑能量剖面和最大升阻比下滑能量剖面在自动着陆窗口归于一点，动压剖面和能量走廊如下：

图1 能量走廊及动压剖面规划Fig.1 Energy corridor and design of dynamic pressure profile

3.2 标称下滑能量剖面跟踪

标称下滑能量剖面的跟踪策略如图2所示，当在某一待飞距离下，对RLV的能量航程比进行估算，定义KE/W=(E/W)/(E/W)标称，为若其满足 0.9≤KE/W≤1.1，则按照规划的标称能量剖面飞行；若KE/W＞1.1，则切换到最陡下滑可加速能量消耗回到标称下滑能量剖面上；若KE/W＜0.9，则切换到最大升阻比下滑可减慢能量消耗回到标称下滑能量剖面上。

图2 标称下滑能量剖面跟踪Fig.2 Tracking of normal energy profile

4 纵向控制律设计

以俯仰角速率控制作为控制系统的内回路[5]，既能够实现RLV本体的增稳控制，进行高精度的轨迹跟踪控制，又能够实现对RLV进行姿态控制。

RLV无动力下滑时，给飞机的输出指令为舵偏，将俯仰角速率指令转化为舵偏指令：

控制结构如3所示。

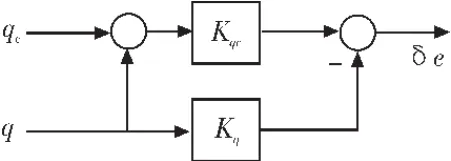
图3 俯仰角速率控制回路Fig.3 Control of pitching rate

高度跟踪通过控制高度变化率实现，高度变化率指令可由高度偏差信号转化得到：

然后将高度变化率的偏差转为法向过载指令：

考虑到不同速度下高度变化率的差异较大，将其转化为俯仰角速率指令：

控制结构如4所示。

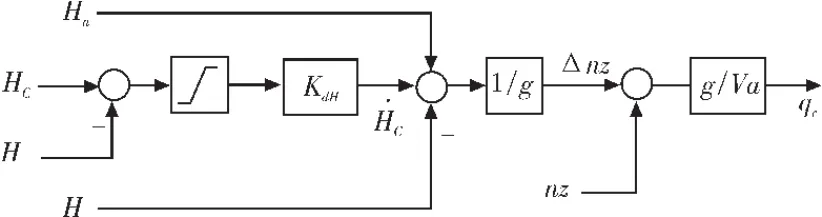
图4 高度控制回路Fig.4 Control of height

5 仿真实例

根据上文提到的轨迹优化方法进行TAEM段轨迹设计，并用文中所设计的高度跟踪控制器进行轨迹跟踪。

选定图1所示标称下滑动压剖面，HTAEM为22 km，QTAEM为 35 kpa，HAL为 3 km，QAL为 8 kpa，则标称动压剖面规划及仿真结果如5所示。

图5 轨迹规划结果与跟踪Fig.5 Design and tracking of the trajectory

由仿真结果可以看出，随着高度的降低，RLV动压逐渐过渡到8 kpa左右，RLV在10 km附近经历跨音速，航迹倾斜角、攻角在跨音速状态时有个转折，航迹倾斜角最终在自动着陆窗口时达到-7。左右，攻角变化范围较小，在满足各种约束的情况下,RLV能很好的跟踪标称能量剖面，到达自动着陆窗口。

6 结论

文中根据末端能量管理段特点，结合末端能量管理段下滑轨迹的设计方法，将下滑轨迹的优化转化为数学优化问题，针对具体的重复使用运载器进行TAEM段的能量剖面设计，并设计相应的高度跟踪控制器对标称能量剖面进行跟踪，设计结果满足高度、动压、航迹倾斜角及攻角等各种约束条件。仿真结果表明此方法能够充分发挥飞行器机动能力，使其到达自动着陆窗口。

[1]Barton G H,Tragresser S.G.Autolanding Trajectory Design for the X-34[C]//AIAA,August 1999:99-4146.

[2]Barton,G.H,New Methodologies for Assessing the Robustness of the X-34 Autolanding Trajectories[C]//American Astronautical Society,2001:1-14.

[3]Hanson John M.A plan for advanced guidance and control technology for 2nd generation reusable launch vehicles[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit 5-8 August 2002,Monterey,California.AIAA,2002-4557.

[4]Girerd,A.R,Onboard Trajectory Generation for the Unpowered Landing of Autonomous Reusable Launch Vehicles[D].S.M.Thesis,Department of Aeronautics and Astronautics,MIT,2001.

[5]孙春贞.重复使用运载器末端区域能量管理与自动着陆技术研究[M].南京：南京航空航天大学，2008.

[6]沈宏良，陶矩，魏立新，等.航天飞机自动着陆轨迹优化设计[J].飞行力学，2004,22(1):10-13.SHEN Hong-liang,TAO Ju,WEI Li-xin,et al.Optimal design of autolanding traj ectory for a space shuttle[J].Flight Dynamics,2004,22(1):10-13.