基于支持向量机的水声信号多分类器设计

刘深

（昆明船舶设备研究试验中心 云南 昆明 650051）

传统的模式识别或人工神经网络都是以大样本统计理论为基础的，而实际操作中常常面对的是小样本。如何从小样本集出发，得到泛化能力较好的模型，是模式识别研究领域内的一个难点。Vapnik等早在20世纪60年代开始研究有限样本情况下的机器学习问题。近年来，有限样本机器学习理论逐渐成熟，形成了完善的统计学习理论（SLT）体系，但也遇到了许多困难，如确定网络结构的问题、过拟合与欠拟合问题、局部极小点问题等。1992到1995年，在SLT的基础上发展了支持向量机（Support Vector Machine，SVM）算法，在解决小样本、非线性及高维模式识别问题中表现出许多特有的优势[1，2]。

水声信号获取不易，而支持向量机对小样本数据具有很好的分类性能，因此解决了水声信号样本不足的问题。同时水声信号类型多样化，对分类器的泛化性能提出了很高的要求，这一点也是支持向量机分类器的优势所在。

1 支持向量机的分类机理

支持向量机利用线性可分或非线性不可分训练样本集，运用最优化理论在原始特征空间中建立最优线性分类界面或广义最优线性分类界面，然后利用满足Mercer定理的核函数代替原始分类界面函数中的内积，不需显式地使用非线性变换的具体形式，将原始特征空间中的非线性分类界面隐式地映射到更高维的变换特征空间中产生线性分类界面，这样可以方便的达到更好的分类效果。

设线性可分样本集为（xi，yi），i=1，…，x，n∈Rd，y∈{+1，-1}是类别标号。d维空间中线性判别函数的一般形式为g（x）=w·x+b，分类面方程为[3]：

将判别函数归一化，使两类所有样本都满足|g（x）|≥1，即使离分类面最近的样本的|g（x）|=1，这样分类间隔就等于2/‖w‖，因此使间隔最大等价于使‖w‖或‖w‖2最小；而要求分类线对所有样本正确分类，就是要求它满足

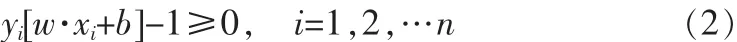
因此，满足上述条件且使‖w‖2最小的分类面就是最优分类面。两类样本中离分类面最近的点且平行于最优分类面上的训练样本就是上式中使等号成立的那些样本，它们就是支持向量，因为它们支撑了最优分类面。

根据上面的讨论，最优分类面问题可以表示成如下的约束化问题，即在式（2）的约束下，求函数

的最小值。为此，可以定义如下的Lagrange函数：

其中，αi>0为Lagrange系数，我们的问题是对w和b求Lagrange函数的极小值。分别对式（4）中w和b求偏微分并令它们等于0，就可以把原问题转化为如下这种较简单的对偶问题：

在约束条件

之下对αi求解下列函数的最大值：

即，最优分类面的权系数向量是训练样本向量的线性组合[4-5]。

这是一个不等式约束下二次函数极值问题，存在唯一解。求解上述问题后得到的最优分类函数是：

式中sgn（）为符号函数。由于非支持向量对应的αi均为0，因此式（8）中的求和实际上只对支持向量进行。而b*是分类的域值，可以由任意一个支持向量用式（1）求得，或通过两类中任意一对支持向量取中值求得。

如果用内积K（x，x′）代替最优分类面中的点积，就相当于把原特征空间变换到了某一新的特征空间，此时，优化函数变为：

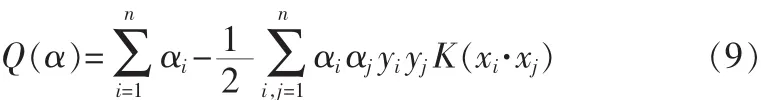
而相应的判决函数式也应变为：

算法的其它条件均不变。这就是支持向量机。

这里的内积 K（x，x′）称为核函数，本文使用径向基函数（RBF）作为核函数。

式（11）中，σ为控制核函数高宽的参数。其满足Mercer条件[6]。

2 基于SVM的多分类器设计

2.1 水声信号分类器设计思路

SVM分类器采用径向基函数作为核函数，可以解决任意维数的特征矩阵的问题。本文主要验证3分类情况。

以下为设计思路：

1）读入样本数据，挑选合适的特征作为训练集；

2）构造3个二分类器，分别计算这3个分类器的权值和偏置系数；

3）输入测试集数据，分别代入3个分类器，计算得出三个信号的分类结果；

4）与该信号实际所属类别比较，计算正确率。

2.2 实际水声信号分类实例

分类数据为实际水声信号，该信号有3类，编号为A、B、C，以矩阵形式存储。

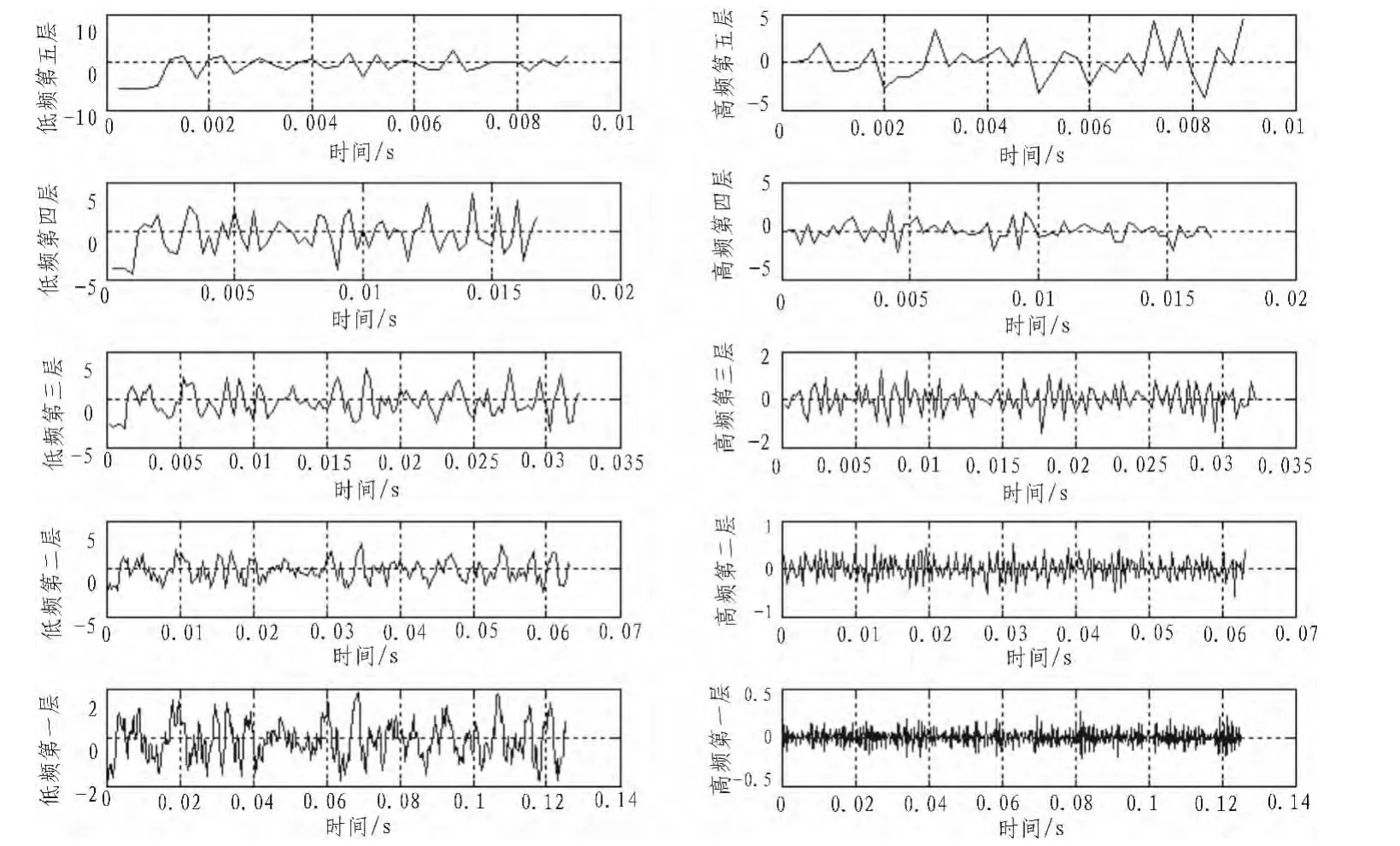
图1 A类第一组信号小波系数图Fig.1 First group of wavelet coefficients of A class

图2 B类第一组信号小波系数图Fig．2 First group of wavelet coefficients of B class

图3 C类第一组信号小波系数图Fig．3 First group of wavelet coefficients of C class

本节采用改进的支持向量机分类程序，重新设计了3类分类器，并进行了分类实验。过程如下：

1）实际水声信号的预处理：

信号预处理包括对信号的降噪、滤波等，不是本文重点，因此不做详细介绍。

2）实际水声信号的特征提取：

对实际信号进行分段、截取，将截取到的一段信号进行五层小波分解，得到各层小波系数，做出三类信号的功率谱，作为一个特征值。重复上述过程，直到将截取到的信号段的特征提取完为止。本实验中选取的截取长度为1 000点，实际信号长度为32 000个点，采样频率为4 kHz。现以A、B、C三类信号的第一段为例。

①实际信号小波分解图（仅对A、B、C三类的第一组详细介绍，第二、三组与第一组类似）如图1～3。

图1～3中，从上到下依次为第五层、第四层、……、第一层小波系数，左侧为低频小波系数，右侧为高频小波系数。

②三类信号的功率谱，如图4～6所示。

图4 A类第一组信号功率谱图Fig．4 First group of signal power spectrum of A class

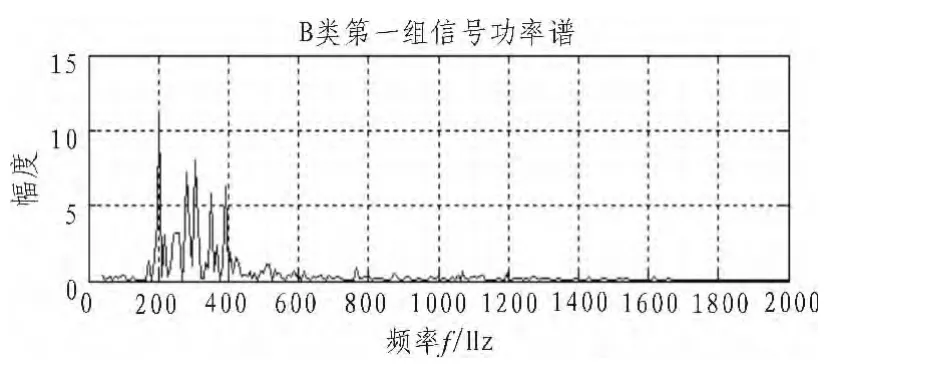
图5 B类第一组信号功率谱图Fig．5 First group of signal power spectrum of B class

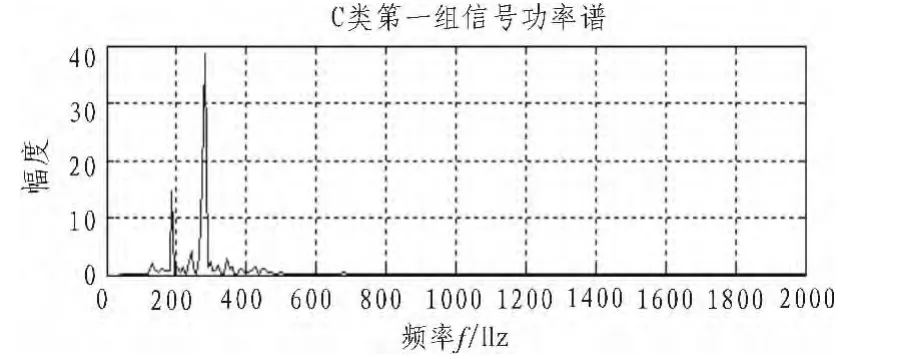
图6 C类第一组信号功率谱图Fig．6 First group of signal power spectrum of C class

观察三类信号的功率谱图可以发现，三类水声信号的能量主要集中在低频段，大概在 50～500 Hz之间，所以选择低频第一层、第二层和第三层小波系数就可以描述信号特征。

3）实际水声信号的分类：

实际信号有A、B、C 3类，提取出来的特征矩阵共有三个样本集，每个样本集为的矩阵。我们从中随即选取10组样本作为训练样本，剩下的20组为测试样本。表1为多次独立试验平均分类准确率。表2为使用神经网络分类器进行多次独立试验的试验结果。

对比表1和表2可以发现在相同训练样本和测试样本条件下，SVM多分类器的分类效果要优于神经网络分类器，证明了本文设计的SVM分类器的有效性，也从侧面验证了SVM分类器在处理小样本数据时的优越性。

表1 SVM分类器多次独立重复试验结果Tab.1 Independent repeated trials result of SVM classifier

表2 神经网络分类器多次独立重复试验结果Tab.2 Independent repeated trials result of neural network classifier

3 结 论

本文初步研究了基于支持向量机的分类器在多类水声信号分类问题中的应用。该方法有效的避免了“维数灾难”，可以较好的解决多类水声信号的分类问题，使得算法复杂度可以不随维数的增加而增加。但是本文也有不足，由于水声信号提取难度较大，本文只验证了三分类的情况，若以后获得其他水声信号数据，本文作者将做更深一步的研究与验证。

[1]周绮凤．基于支持向量机的若干分类问题研究[D]．厦门:厦门大学，2007．

[2]孙即祥．现代模式识别[M]．2版．高等教育出版社，2008．

[3]肖健华．智能模式识别方法[M]．广州:华南理工大学出版社，2006．

[4]王国胜．支持向量机的理论与算法研究[D]．北京:北京邮电大学，2007．

[5]王晓丹，王积勤．支持向量机和实现算法综述[J]．计算机工程与应用，2004，40（13）:75－78．WANG Xiao-dan，WANG Ji-qin．A survey on support vector machines training and testing algorithms[J]．Computer Engineering and Applications，2004，40（13）:75－78．

[6]罗林开．支持向量机的核选择[D]．厦门:厦门大学，2007．