基于Z脉冲信号的高速高精回零方式研究

王兴飞，郑仲谦，李 松

（华南理工大学 机械与汽车工程学院，广东 广州 510640）

随着电子信息技术的发展，数字化制造技术越来越成为机电一体化时代机床业的核心技术，其代表产物就是数控机床。数控机床可以在提高生产率的同时，保证产品一定的加工质量和加工精度。加工过程中机床各个轴都设定了一个原点，作为轴运动的零点。确定零点位置对机床的精度是至关重要的，回零操作就是要确定位置测量的起点，数控机床的刀具补偿、反向间隙补偿、螺距误差补偿等精度补偿措施能否发挥作用，也完全取决于数控机床的回零精度[1]。

回零方式根据检测装置的不同，可以分为栅格法和磁开关法两种[2]。其中光电开关加光栅尺或者旋转码器是最常使用的回零方式。由于光电开关有一定的宽度，所以可以利用光栅尺和旋转编码器的Z脉冲信号精确回零。实际应用中一般将回零分为高速寻找光电开关和低速寻找Z脉冲信号两个阶段。然而随着回零速度的提高，运动轴切换不同速度时，会出现震动现象，并且会因为轴减速产生的一定减速距离而不能在Z脉冲信号处精确停止。

本文针对如何消除高速运动下，轴启停产生的震动和提高回零精度两方面阐述改进后的回零过程优化方案。该方案经过实验仿真和实际测试证明，有效的提高了运动的平稳性、速度和精度，并已成功应用于东莞市升力智能科技有限公司自主研发的通用运动控制卡中。

1 回零速度规划的改进算法

为解决高速运动状态下电机的震动现象，在运动开始和结束时，需要加减速过程。梯形速度规划算法和S形速度规划是最常见的两种速度规划算法。其中由于S形速度规划的柔性、连续性好，而成为比较理想的速度规划算法[3-4]。

S形速度曲线一般被抽象为7段式模型，即整个运动被分为加加速段、匀加速段、减加速段、匀速段、加减速段、匀减速段和减减速段，分别对应图1的①到⑦各个阶段。

其中，vs为起始速度，ve为终点速度，V为指定的目标速度；τk（k=1，2…7）为局部时间坐标，表示以各个阶段的起始点作为零点的时间表示，τk=t-tk-1。速度规划过程中位移、速度、加速度和加加速度的关系可用式（1）、（2）、（3）表示。

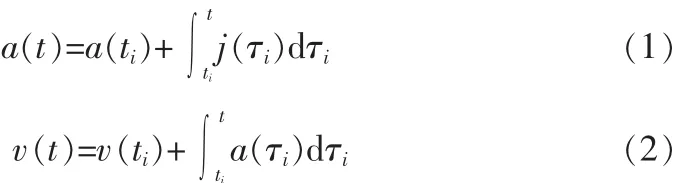
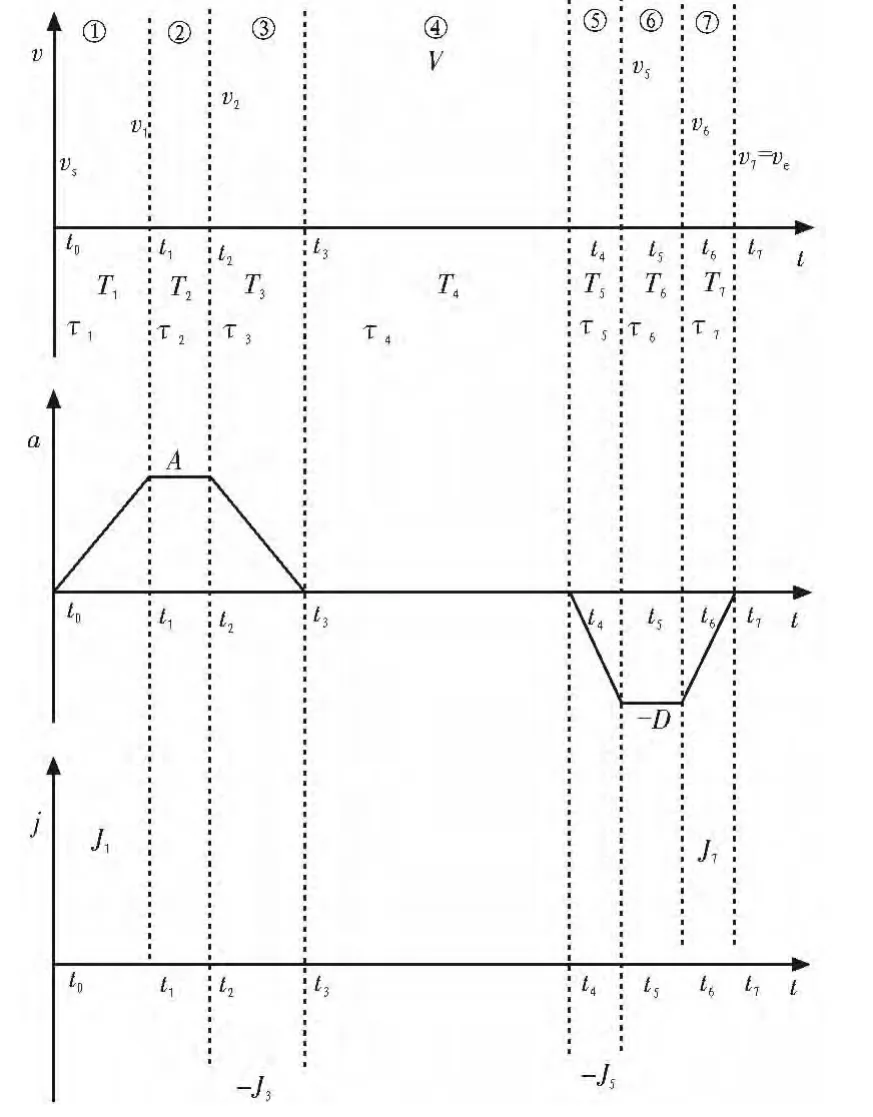
图1 7阶段S形速度规划示意图Fig.1 Schematic of 7 stage S-curve velocity planning

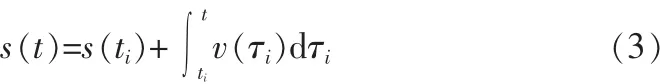
然而在此种速度规划算法中，需要指定运动长度L、目标速度V、最大加速度A、最大减速度D以及第 1、3、5、7阶段的加加速度 J1、J3、J5、J7[6-8]，才能完成整个速度规划算法，这个过程计算量大，算法的程序实现复杂。而在某些情况下，若目标速度V太小，可能导致T2和T6等于0，也就是不存在匀加速和匀减速阶段；若指定的运动长度太短，也可能导致T2、T4和T6等于0，也就是不存在匀加速，匀速和匀减速阶段。这时7阶段模型就简化为了5阶段模型，其速度、加速度、加加速度关系如图2所示，由图可以看出，精简以后的速度曲线的各个阶段仍然平滑过度，满足柔性控制方法的要求。

在实际应用中，经常用指定加减速时间的方法来代替设定加速度和加加速度等概念比较抽象的参数。如果假设7阶段速度规划模型中加速时间为，减速时间为，并且①和③、⑤和⑦阶段加加速度分别相等，即J1=J3，J5=J7，。那么可知T1=T3，T5=T7，J1T1=J3T3=A，并且存在以下关系式（3）和（4）。

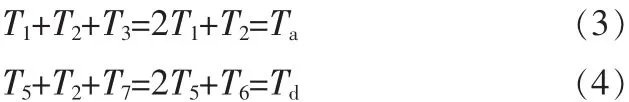
对于由①加加速段、②匀加速段、③减加速段三段组成的加速过程，可得如下关系：

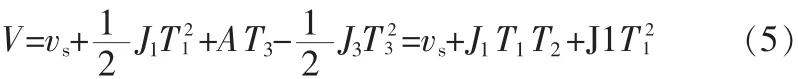
由方程（5）可看出，在加速过程中无法全部解出T1、T2和T1，即在7阶段模型中无法通过直接指定加减速时间来实现S形加减速规划。在5阶段模型中，由于没有匀加速阶段和匀减速阶段，方程（5）可以解出T1和J1。因此，5阶段模型可以在只指定运动距离L、目标速度V、起始速度vs、终止速度ve、加速度时间Ta和减速度时间Td6个变量情况下完成速度规划，并且保证运动的平稳性。

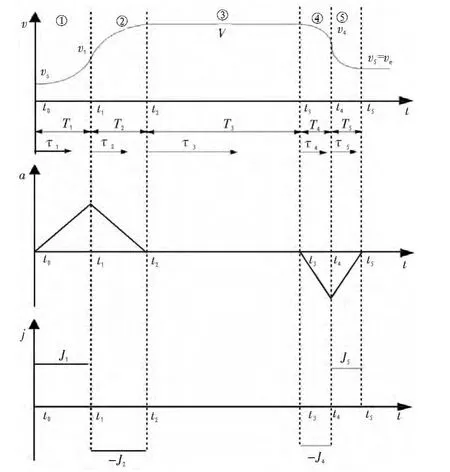
图2 5阶段S形速度规划示意图Fig.2 Schematic of 5 stage S-curve velocity planning

2 回零过程状态分析

在某些回零速度要求较高的场合，由于最后寻找Z脉冲信号阶段的速度仍然很高，捕捉到Z脉冲信号时不能及时停止，导致回零精度降低。为解决这一问题，对常用的基于Z脉冲的回零方式进行了改进，即在回零最后阶段Z脉冲产生时利用高速锁存器锁存精确的零点位置。当回零轴停止后，再根据当前位置和锁存位置进行误差补偿，以保证较高的回零速度下的回零精度。改善方案的回零过程如图3所示。

由于各轴运动的起始位置不确定，所以把起始位置分为了在特殊位置和不在特殊位置，特殊位置又包括在零点和正、负限位处，3种情况。

当起始点不在特殊位置时，按照设定的回零方向寻找零点开关。在运动过程中采用周期查询的方式获取各轴的位置信息。如果在回零方向上首先遇到了零点开关，则会减速停止。然后，以回零低速向Z脉冲信号存在的方向离开零点开关。当离开零点开关的瞬间又以这个速度向指定方向寻找Z脉冲信号。在检测到Z脉冲信号时，触发高速锁存器锁存当前编码器的位置信息，同时使轴立即减速停止。轴停止后再次读取编码器的位置信息，并将两次的读数相减，即可得到当前位置到Z脉冲点的偏差。最后再让电机向反方向旋转此偏差的距离，以补偿减速停止后的误差。至此清除相关寄存器的数值，整个回零过程结束。如果在遇到零点开关前先遇到了限位开关，则需要另电机反向旋转继续寻找零点，找到零点后的运动过程和上面的过程相同。

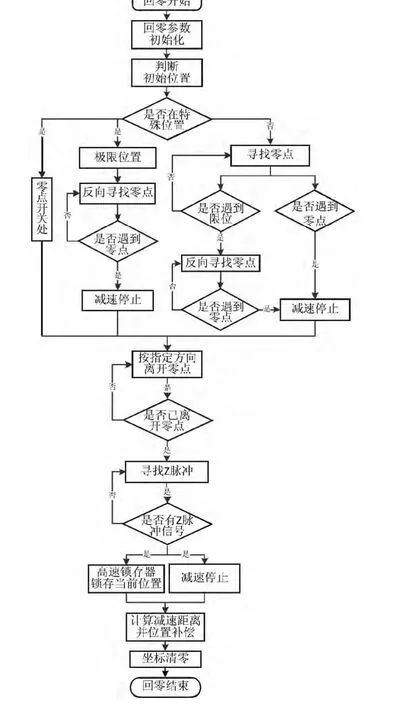
图3 回零过程流程图Fig.3 Flowchart of homing process

当起始在特殊位置时，如果在零点处，则直接重复上述的过程；如果在极限开关处，则需要向极限开关的反向运动寻找零点，到零点后同样重复上述过程。

3 试验验证

为检验5阶段速度规划曲线的连续性和平滑性，对速度规划算法进行了软件的多次仿真测试，其中一次的仿真结果如图4和图5所示。

经过多次仿真实验后可以看出，简化后的5阶段速度规划曲线仍然可以保证速度和加速度的连续性和平滑性，可以满足柔性控制的要求。并且在实验平台运行过程中，随着速度的提高，依然可以平稳运行。

为检验回零的准确性，搭建了图6所示的实验平台，零点开关安装在Z脉冲信号的左侧。程序设计时已经确定了回零的起始方向，并且是固定的，这里设定的为负方向。

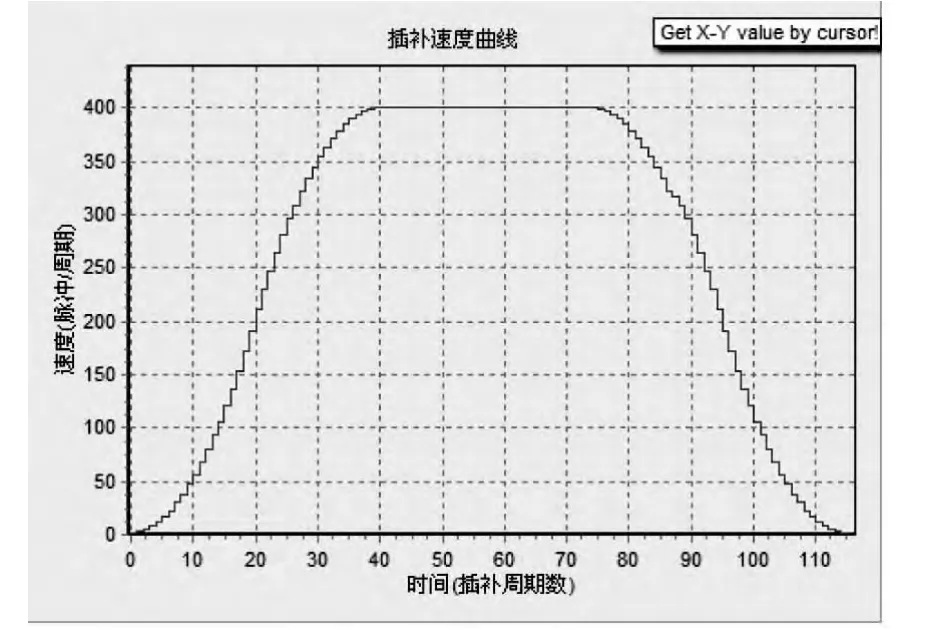
图4 5阶段速度规划速度曲线仿真图Fig.4 Velocity simulation diagram of 5 stage velocity planning

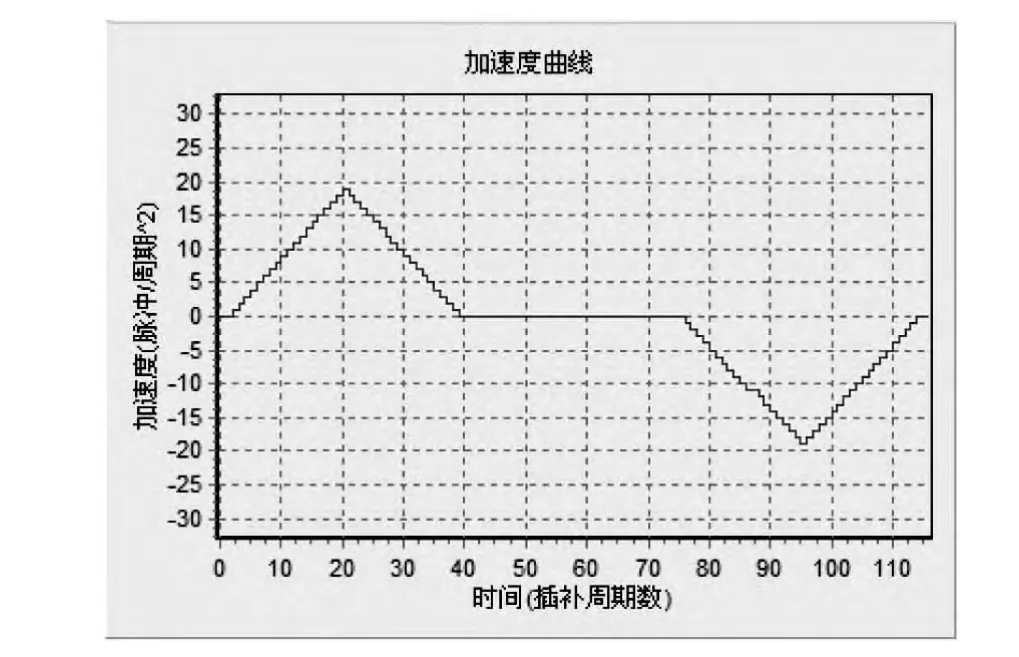
图5 5阶段速度规划加速度曲线仿真图Fig.5 Acceleration simulation diagram of 5 stage velocity planning

图6 旋转编码器方式回零示意图Fig.6 Schematic ofrotary encoder homing

如果从①位置开始回零，则运动轴将先以高速向负方向寻找零点。当遇到零点开关后减速停止，并开始以低速继续前进至越过零点。越过了零点以后开始继续以低速向负方向运动，遇到Z脉冲以后立即停止。如果从②位置开始回零，在这种情况下会先遇到负限位，这里需要在负限位出将轴运动方向调转，并继续寻找零点。当到达零点开关后减速停止，并以低速再次反向运动，直到离开零点开关。然后继续以低速寻找到Z脉冲信号后，轴立即停止。轴停止后，根据当前位置和锁存位置加以补偿，回零结束。

回零过程的改善方案，是针对回零的最后一个阶段，也就是低速找Z脉冲的阶段提高速度后精度降低提出的。为测量有无高速锁存以及回零最后阶段的速度对回零精度的影响，在实验中采用了激光干涉仪测量回零结束后的位置误差。试验分为低速无锁存、相对较高速度无锁存和相对较高速度有锁存三种情况分别测量。实验中设定速度值与测量的部分结果如表1所示。

从试验数据可以看出，当Z脉冲处没有高速锁存时，回零最后一个阶段的速度越大误差也越大。速度为0.2 m/s时误差已经达到了80 μm左右。而贴片机、FPC补强机等高精度机床的最低精度要求也需要达到50 μm以内。随着速度的不断提高误差将进一步增大，显然没有高速锁存的情况下，回零最后一个阶段必须较低的速度。然而，在Z脉冲处触发高速锁存的情况下，即使速度提高到0．5 m/s都可以很准确的定位到零点，而且回零误差在1～2 μm左右。由此可见，此时回零精度即可满足部分高精度机床的要求。

表1 不同条件下回零精度对比Tab.1 Comparison of homing accuracy in different conditions

4 结束语

通过在实际机床中大量测试，结果表明以上提出的解决方案，提高了回零的速度，消除了高速运动下的震动现象，并同时保证了较高了精度。此回零方式配合反向间隙补偿、螺距误差补偿等补偿算法即可满足机床自动运行过程中的精度要求。回零精准是自动化设备能够实现高精度运行的重要前提，因此本方案为高速高精自动化设备的研发打下了良好的基础，并可以推广应用至光栅尺等其他回零方法中。

[1]邹金桥，姜晓强，徐文源．基于数控机床栅格法回零机制的分析及故障诊断[J]．组合机床与自动化加工技术，2006（11）:63－64．ZOU Jin-qiao，JIANG Xiao-chao，XU Wen-yuan．The analysis and fault diagnosis of returning home with grid method based on CNC machine tools[J]．Modular Machine Tool&Automatic Manufacturing Technique，2006（11）:63－64．

[2]陈伟娜．基于DSP的运动控制算法研究与实现[D]．华南理工大学，2012．

[3]朱晓春，屈波，孙来业，等．S曲线加减速控制方法研究[J]．中国制造业信息化，2006，35（23）:38－40．ZHU Xiao-chun，QU Bo，SUN Lai-ye，et al．Study on the accelaration/decelaration control method for S －curve[J]．ManufactureInformation EngineeringofChina，2006，35（23）:38－40．

[4]郭新贵，李从心．S曲线加减速算法研究[J]．机床与液压，2002（5）:60－62．GUO Xin-gui，LI Cong-xin．Studying S－shape acceleration/deceleration algorithm[J]．Hydromechatronics Engineering，2002（5）:60－62．

[5]KaanErkorkmaz，AltintasY．High speed CNC system design:Part I:jerk limited trajectory generation and quintic spline interpolation [J]．International Journal Machine Tools&Manufacture，2001，41（9）:1323－1345

[6]胡鸿豪．CNC系统直线加减速优化算法[J]．机床与液压，2008，36（5）:287－289．HU Hong-hao．Linear acceleration and deceleration optimization algorithm for CNC machine tools[J]．Hydromechatronics Engineering，2008，36（5）:287－289．

[7]李晓辉，邬义杰，冷洪滨．S曲线加减速控制新方法的研究[J]．组合机床与自动化加工技术，2007（10）:50－53．LI Xiao-hui，WU Yi-jie，LENG Hong-bin．Research on a new S －curve acceleration and deceleration control method[J]．ModularMachineTool&AutomaticManufacturingTechnique，2007，10:50－53．

[8]赵光．CNC插补过程中加减速控制算法的研究[D]．济南：山东科技大学，2007．