数学建模：提升高等数学教学效率的有效途径

李栋红

（阳泉师范高等专科学校，山西 阳泉 045200）

高等院校中，数学是一门基础性课程，占据高等院校课程体系的特殊地位，高等数学能够为后继课程提供有效的应用工具与基础数学知识，对培养大学生的能力具有重要作用。但是，由于现代社会信息化程度不断提高，当今教育也对高等数学教学的要求更高。比如，在构建课程体系、设置教学内容等方面必须有新突破，不断改革数学教学模式、手段以及方法，为社会培养出独具创新意识的现代化应用人才。此外，由于高等教育的普及化与大众化，而且高等院校招生规模也在不断扩大，使得其总体生源素质呈现下降趋势，尤其是高职院校学生存在非常薄弱的数学基础。对于此现象，如何提升高等数学教学效率，与时代发展和进步需求相适应，是目前高等数学教学中需要探讨的问题。因此，论文将有效结合高等数据教学实践，对提升高等数学教学效率的有效途径进行分析与探讨。

一、高等数学教学中数学建模的作用

（一）激发学生学习高数的兴趣

学生能够在学习数学过程中对通过数学理论与方法去分析与解决实际问题有所了解，提高其解决和分析问题的水平与能力，并在某种程度上提高学生数学应用意识与数学学习主动性，保证学生在未来工作中能够以数学的思维解决实际问题。正所谓对材料感兴趣能够帮助学生学习。数学建模教学能够将更多有效的学习材料提供给学生。就现实视角与社会发展现状来说，社会的发展需要大学生一定要具备高数学素养。若学生具有较低的数学素养，则该学生就难以在工程与科技等领域有所贡献与作为。现阶段一些学生存在畏惧数学心理，认为学习数学是一种噩梦，还有些学生认为数学仅仅是学位与考试的代名词，并没有特别大的用处，要想端正这种思想，一定要从数学源头与解决实际问题着手。对数学模型进行学习与应用的思维属于一种行之有效的措施，因为学生在建模中能够切身领悟到数学是科学范畴，由此就能带给学生一种对解决问题的有效方式。

（二）提高学生数学适应能力、应用能力和综合素质

从根本上说，数学建模是科研活动的范畴，而且对学生今后的工作和学习极具深远影响，同时对学生水平和能力也有更高要求，对数学建模竞赛活动和思想予以普及，不仅能够在某种程度上提高学生对数学进行应用的能力，培养学生创造性思维能力与合作意识，同时还能促进高校教学改革和课程建设，以此激发学生本身所具有的创新精神。对于学生而言，数学建模是联系实际问题与理论数学的重要桥梁。因此，在数学教学过程中，首先，必须积极引导学生对数学背景和知识内容进行学习，以此加深学生对数学问题进行理解的能力，进一步拓展学生知识面，最终提高学生数学水平。其次，必须在学习数学模型中培养学生运用数学的能力与意识。通过对数学模型的学习，参与数学建模，以此增强学生数学应用意识，并在一定程度上提高学生通过数学对实际问题予以解决的能力。

二、高等数学教学中数学建模的应用

通常在高等数学教学中都会忽视数学定理几何意义与数学现象中的几何背景，而是直接向学生传达数学定理与定义，同时将其应用在高数解题思路中，不重视高数知识形成过程与应用的解释和揭示，几乎不会顾及到微积分和几何联系的紧密性，这对提高学生数学素质具有非常大的影响。根据此现象，在高等数学教学过程中必须注重与某些定理、概念以及题目的建模意义进行有效结合，对学生作针对性授课，以使数学建模在高数教学中的重要作用得到充分发挥。

1.通过数学建模解决数学问题

将初看起来杂乱无章的实际问题抽象为一个数学问题是数学建模的主要目标。数学建模中，对于错综复杂的实际问题，需要建模者对其主观能动性进行充分发挥，探索与发现问题，创造性地用形式或似真推理，对观察、实验、类比、联想、归纳、直觉和审美等多种思维方式进行综合利用，以达到解决问题的目的。将客观实际与数学问题联系起来的纽带首先是数学建模，也就是说，用数学语言（由数字、数学符号、字母组成的图表、公式或程序）来描述实际问题中的数量关系、空间形式。它主要通过建立数学模型，及解决各种实际问题等形式来考察大学生的数学修养、应用能力和创新精神。数学模型就是对实际问题的一种数学表述。确切地说，数学模型就是对于一个特定的对象，为了一个特定目标，根据特有的内在规律做出一些必要的简化假设，并运用适当的数学工具得到的一个数学结构。数学结构可以是数学算法、公式、表格、图示等。数学建模是一种数学的思考方法，是运用数学的语言和方法，通过简化、抽象建立能近似刻划并解决实际问题的一种强有力的数学手段。比如，求解曲边梯形面积引申出“定积分”的定义，为了使学生更为清晰直观地了解形成“定积分”概念的过程，可以采用“取近似、作分割、取极限以及求和式”等相关建模操作，同时以动画演示的方式在分割区间处于[a,b]时，Sm与积分会随着n的进一步扩大，逐渐向曲边梯形面积S逼近的过程，由此在对面积求解予以完成的同时，也会将定积分概念引申出来。这样能够有效揭示定积分概念产生的背景，对学生对概念的正确把握与理解非常有利，同时进一步深化了高等数学教学中的概念教学。

2.在数学几何公式中应用数学建模

一般微积分定理中都有相应的几何背景与几何意义，如果可以对其几何意义进行充分利用，将形与数所特有的内在联系充分揭示出来，以构造辅助函数的关系，能够保证定理及时获证。比如，证明微积分中值定理其实就是利用定理几何意义，通过构造高数辅助函数，即，将其转化为罗尔定理，最终得出结论。

在高等数学中，所计算出来的多数问题都非常有难度，而且十分繁琐，如果可以通过数学建模使学生思维得到启迪，将对高数问题的解答极为有利。对于所计算的一些重积分，若可以将被积函数的奇偶性与区域对称性进行有效结合，能够使复杂而抽象的数学问题更为直观与形象，进一步降低解题难度，化繁为简，这样能够将积分值快速求出来。

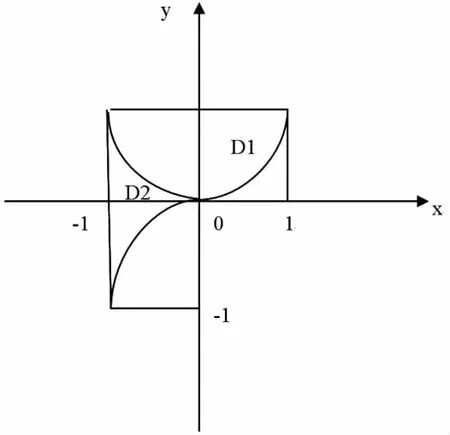
分析：因为被积函数中含有抽象函数，即f（x2+y2），所以，不能对其作直接性积分，然而，一定要注意被积函数中（x，y）=xyf（x2+y2）与以下条件相满足：

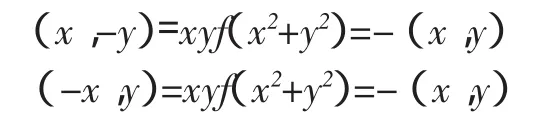
也就是说，（x，y）中的变量函数x属于奇函数，而变量函数y同样属于奇函数，依照对称区间中奇函数的定积分性质，若区域存在对称性，那么就能够简化积分计算。将积分区域画出来，观察可知，采用曲线y=-x3能够将区域进行x轴对称区域D2与y轴对称区域D1，以此依照区域中积分的可加性得出

三、数学建模应用于高等数学教学汇总需要注意的问题

（一）以高等数学教学为主，数学建模为辅

根据课堂教学地位与主要内容，将高等数学视为课堂教学的基本内容。从根本上说，数学建模被称为学生认知的有效途径，并服务于高等数学教学，同时也是数学教学的补充与延伸，具有从属作用。所以，应该以高等数学为主，数学建模为辅，两者避免出现本末倒置与平分秋色的情况。所以，将数学建模方法与思想融入到高数教学的问题，其实就是将数学建模理念所渗透的高数教学量避免超过一个度，不然，高等数学课可能就会演变为数学建模课。所以在数学教学具体实践中，一定要注意区分数学教学内容与课型，避免出现由于学生偏好数学建模而对课型做任意改变，适当运用数学建模。

（二）引入数学建模时机要恰当

将数学建模理念以合理顺序融入高数教学中，可以说这是一门学问。不是每一个高数教学都必须将建模方法融入进去，也不比在一整堂课中始终贯穿数学建模，必须与高数教学内容进行有效结合，由浅入深、循序渐进地推介各种数学建模措施。

（三）和高等数学知识相匹配

一般情况下，学生要想全面掌握数学建模方法与内容，通常需花费很多时间，而高等数学课时极为有限，所以如何在有限时间内将高数教学任务高效完成，将数学建模融入进去，对高数教学效果与效率有何影响等等，都是值得高数师生深思的问题。由此可见，建模方法范畴必须做到和高数知识相匹配。若数学建模案例内容在所学高数范畴之外，那么必须耗损有限的时间资源，这就等于说是忙中添乱，最终导致适得其反的教学效果。例如，在对无穷级数12，212，123…进行教学时，可以进入《庄子》语录：“一尺之锤，日取其半，万世不竭”；在向学生传授定积分定义时，可将求曲边梯形面积当做原型。

[1]沈澄.高职高等数学多媒体教学的心理机制与思考[J].湖南农业大学学报（社会科学版·素质教育研究），2008（5）:120-121.

[2]程红萍.试论高职院校高等数学教学改革[J].陕西教育（高教版），2011（4）:154-155.

[3]周巧姝,张朝燕.高等数学课多媒体教学的研究与实践[J].长春师范学院学报（自然科学版），2008（8）:184-186.

[4]金辉.数学建模与高等数学教学改革[J].江苏经贸职业技术学院学报，2006（4）:187-189.

[5]颜冠群.论在文科高等数学教学中引入数学建模思想[J].江苏经贸职业技术学院学报，2010（5）:147-148.