求解非对称线性方程组的自适应简单GMRES(m)算法

2014-01-20王雅

烟台职业学院学报 2014年4期

关键词：线性方程组范数非对称

王雅

(常州市广播电视大学信息与工程学院数学部，江苏常州213001)

求解非对称线性方程组的自适应简单GMRES(m)算法

王雅

(常州市广播电视大学信息与工程学院数学部，江苏常州213001)

GMRES方法比较多的运用于求解大型稀疏非对称线性方程组。本文研究具有自适应重新开始参数的简单GMRES算法，该算法具有储存量少，收敛速度快的特征。文章给出了数值试验和数值比较，以表明新算法的优越性和有效性。

线性方程组;重新开始GMRES;简单;自适应

1 引言

科学技术与生产实际中的大量问题往往归结为求解线性方程组，而且经常是大规模稀疏非对称方程组，广义最小残量法(一般简称GMRES)是目前最为流行并且行之有效的方法之一。求解线性方程组

AX=b

其中A∈Rnxn非奇异，b∈Rn。重新开始GMRES (m)算法可以克服GMRES算法中计算量和存储空间随着迭代步数的增加变得不可接受的情况，确保运算不会中断。

算法1:重新开始GMRES算法，即GMRES(m)

①开始:给定m＜＜n，选取x0，计算r0=b-Ax0及v1=r0/‖r0‖;

②迭代:对j=1，2，…，m

③构造近似解:

计算xm=x0+Vmym，其中 yk是最小二乘问题的解;

④重新开始:

计算rm=b-Axm，若满足精度则停止;否则置x0:=xm，v1=rm/‖rm‖，转第2步。

2 自适应简单GMRES(m)算法

在算法执行过程中，为了提高数值稳定性，每次迭代开始时的初始残量都要规范化，这就要求每次迭代过后，要在校正值上乘以初始残量范数，从而得到重新开始简单GMRES算法SGMRES(m)，下面引入自适应简单GMRES(m)算法。首先，定义两个术语:用连续角(如∠(ri+1，ri))来表示两个连续残量之间的夹角，用跳跃角(如 ∠(ri+1，ri-1))来表示每隔一个残量的两个残量间的夹角。我们计算的角度总是介于0到90度之间的。

这个改变重新开始参数的方法，包括要详细地给定最大与最小的重新开始参数mmax和mmin，相应地，任意第i次迭代重新开始参数mi都要满足mmin≤mi≤mmax。我们把改进的SGMRES(m)记为SGMRES(mmin，mmax)，首次迭代循环以mmax为重新开始参数。然后，我们在每次要重新开始之前计算连续角，来决定下一次的重新开始参数mi。事实上，我们每次都以d小幅度地降低重新开始参数，直到mmin。另外，我们也可以增大mi到mmax。然而，如果连续角很大(接近90度)，表明收敛性良好，那我们就不需要改变当前的重新开始参数了。相反，如果连续角很小(接近0度)，那我们就将之变为mmax。

算法2:自适应简单GMRES算法 SGMRES (mmin，mmax)

cr=1; /*收敛率*/

max_cr=cos(8); /*cos 8°≈0.99*/

min_cr=cos(80);/*cos 80°≈0.175*/

d=3; /*自适应重新开始参数的步长*/

i=0; /*计算迭代次数*/

x=0; /*初始估值*/

r=b-Ax; /*残量*/

while(不收敛)

/*计算重新开始参数mi*/

if(cr＞max_cr or i==0)/*首次迭代或接近停滞*/

mi=mmax

else if(cr＜min_cr)/*收敛率良好*/

else/*调整m*/

if(mi-1-d)≥ mmin

mi=mi-1-d

else

mi=mmax

end

/*重新开始迭代循环*/

for j=1:mi

/*SGMRES迭代*/

/*(如果达到收敛标准则跳出)*/

end

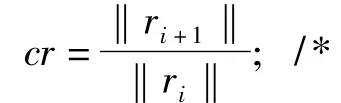
i=i+1;计算收敛率*/

end

从算法2中，很明显可以看出SGMRES(mmin，mmax)的测试标准计算量的简单性，以致可以忽略不计。而且，通过这种方法，我们可以简单迅速地把现有的SGMRES(m)实施改编为一个自适用重新开始的算法。

3 数值试验

此部分通过数值试验，比较GMRES(m)，SGMRES(m)以及SGMRES(mmin，mmax)三者收敛性等，对所有的方程组，我们取方程组右端项b=(1，1，…，1)T，初始估计x=(0，0，…，0)T。并且，GMRES(m)和SGMRES(m)算法的重新开始参数m均取30，SGMRES(mmin，mmax)算法的参数最大值为30，最小值为3，收敛性的判断标准为tol=10-6，即当‖r‖≤tol时结束迭代计算。

例1:矩阵bfw398a.这是一个398×398的矩阵，有3678个非零元素。

当取m=30，mmax=30，mmin=3，d=3，收敛标准为tol=10-6时，分别运行各版本GMRES程序，我们得到了关于矩阵bfw398a的比较，计算结果见表1.