一类分块矩阵的群逆

丁 华

(扬州职业大学，江苏 扬州 225009)

1 定义与引理

定义［8］设A∈Cn×n，若矩阵X 满足如下矩阵方程

则称X 为A 的群逆，记为A#.

引理1［8］设A∈Cn×n，当且仅当ind(A)=1 时，A 的群逆存在.当A 的群逆存在时，A 的群逆唯一，且A#=A(A3)(1)A.

引理2 设A，B∈Cn×n，A2=A，B2=B，R(A)=R(B)，rankA=rankB=r.则存在n 阶酉矩阵U，使得

证明 因为A2=A，B2=B，所以A，B 的特征值均只有1 和0，R(A)，R(B)分别为A，B 关于特征值1的特征子空间.又R(A)=R(B)，rankA=rankB=r，故A，B 关于特征值1 的特征子空间相同，且维数为r.取R(A)=R(B)的一组标准正交基e1，e2，…，er，将其扩充成Cn的标准正交基e1，e2，…，er，er+1，…，en.令U=(e1，…，er，er+1，…，en)*，则U 为n 阶酉矩阵，且

因为rankA=rankB=r，所以A1=0，B1=0，从而

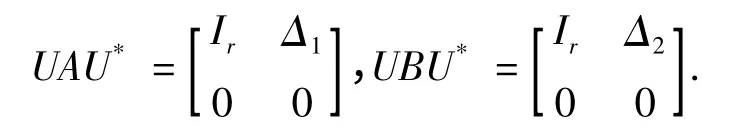
引理3 设A，B∈Cn×n，A2=A，B2=B，R(A)=R(B)，则rankBAB=rankB.

证明 由引理2 的证明可知，R(A)，R(B)分别为A，B 关于特征值1 的特征子空间. R(BAB)⊆R(B).又∀x∈R(B)，x=Bx=BAx=BABx∈R(BAB);故R(BAB)=R(B)，从而rankBAB=rankB.

2 主要结果

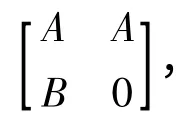
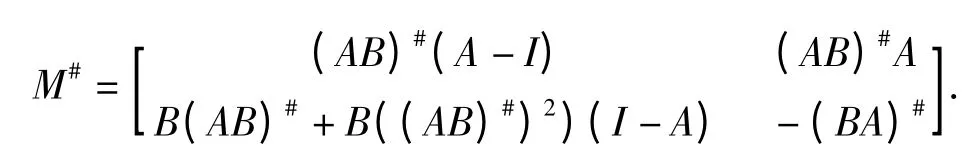
证明 因为

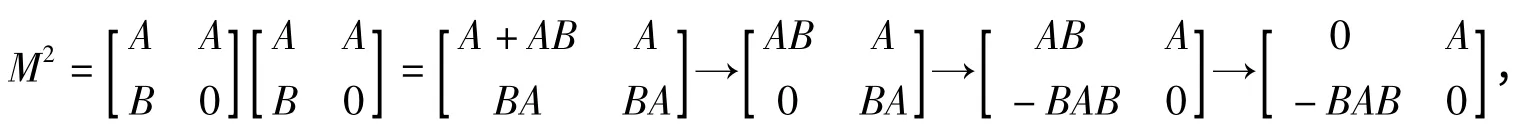
所以由引理3 得，rankM2=rankA+rankBAB=2r.

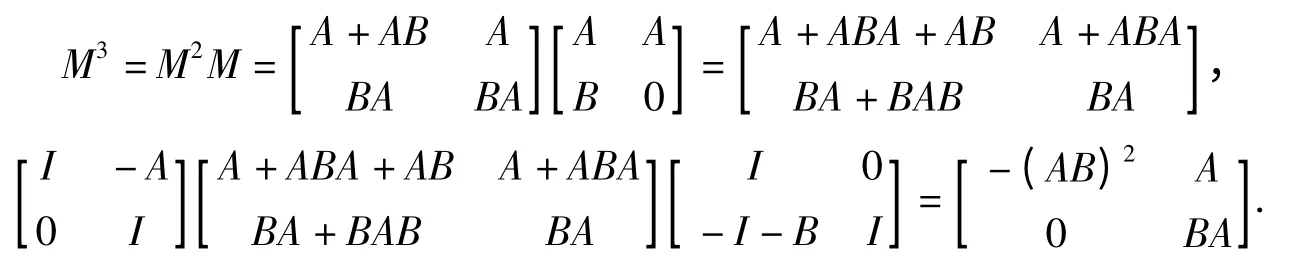
由A2=A，B2=B，R(A)=R(B*)，rankA=rankB=r，根据引理2，存在n 阶酉矩阵U，使得

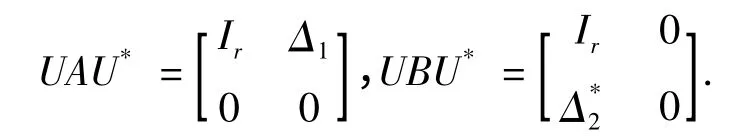
于是，

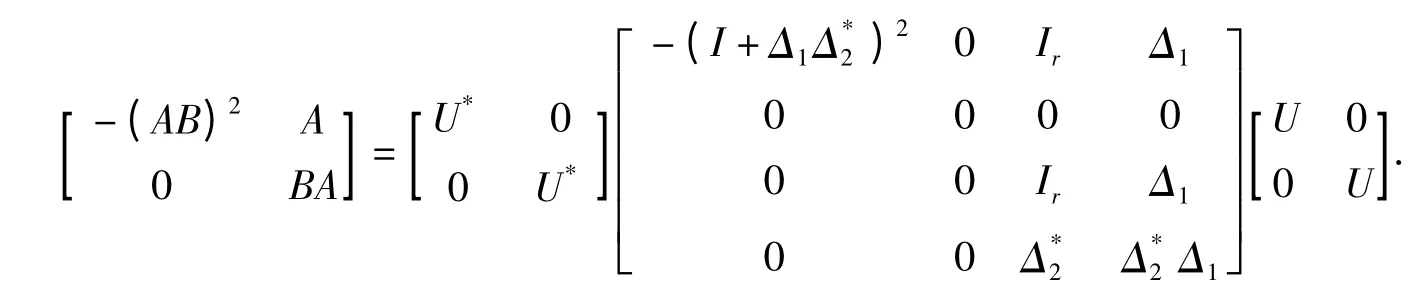
又

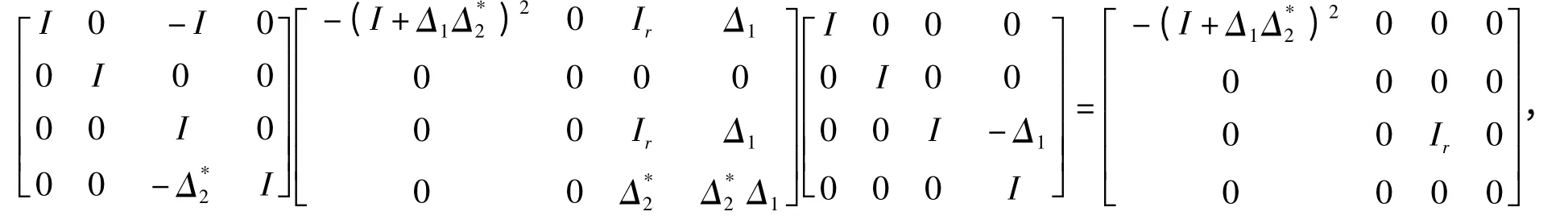
且由rankAB=r 可推出D=I+Δ1Δ*2可逆，从而

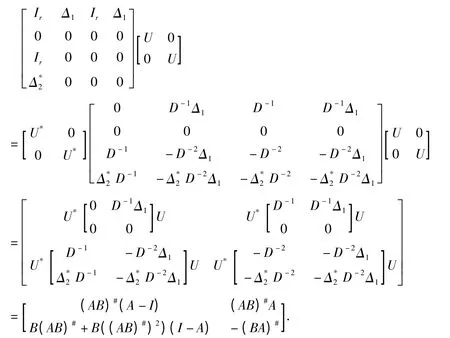
当A∈Cn×n，A2=A，rankA=r 时，A*2=A*，rankA =rankA*=rankAA*=rankA*A =r，故只要在定理中取B=A*，由定理的结论便可得

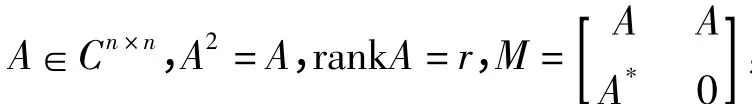
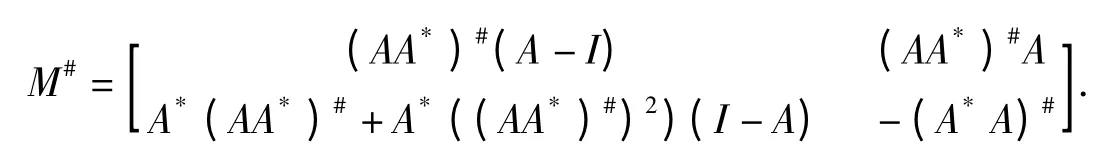
［1］ CAMPBELL S L.The Drazin inverse and systems of second order linear differential［J］.Linear and Multilinear Algebra，1983，14:195 -198.

［2］ 刘玉，曹重光.两类块阵的群逆表示［J］.黑龙江大学自然科学学报，2006，23(3):413 -414.

［3］ 姚红梅，卜长江.一些特殊分块矩阵的群逆［J］.哈尔滨工程大学学报，2008，29(5):529 -532.

［4］ 马元婧，曹重光.分块矩阵的群逆［J］.哈尔滨师范大学自然科学学报，2005，21(4):7 -8.

［5］ 周红玲，王成.特殊分块矩阵的群逆的表示［J］.黑龙江工程学院学报:自然科学版，2013，27(1):78 -80.

［6］ 卜长江，郑金山，赵杰海.关于某些特殊分块矩阵的群逆［J］.哈尔滨工程大学学报，2009，30(9):1074 -1076.

［7］ 宋丽艳.分块矩阵群逆的表示［J］.佳木斯大学学报:自然科学版，2007，25(5):673 -674.

［8］ 何旭初，孙文瑜.广义逆矩阵引论［M］.南京:江苏科学技术出版社，1990.