用等价无穷小代替求极限的推广
2014-01-20姜海勤
姜 海 勤
(扬州职业大学,江苏 扬州 225009)
极限概念是贯穿整个微积分的基本概念,微分、积分、级数等高等数学运算的实质是某种极限运算.等价无穷小代替在求极限过程中有着重要的作用,利用它求不定式极限可以简化计算,使一些复杂的问题简单化.但目前的教材一般只给出两个等价无穷小之比的代换定理,对无穷小代换的使用范围有严格的要求,因而学生在使用时常常会出现一些问题,不明白为什么同样的问题有时通过等价代换可以得到正确的结果而有时又会发生错误[1,2].本文对等价无穷小代换定理的应用范围作了一些推广.
1 乘积函数中的等价无穷小代替
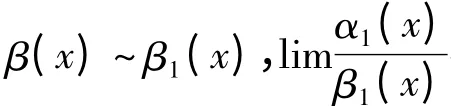
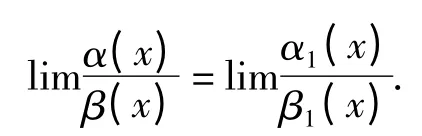
证明见文献[1]、[2].
推论 设α(x),α1(x)是自变量在同一变化过程中的无穷小量,α(x)~α1(x),且lim[α1(x)f(x)]存在,则 lim[α(x)f(x)]=lim[α1(x)f(x)].
证明 若f(x)为非无穷大量,则由无穷小的性质有
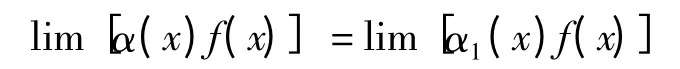
若f(x)为无穷大量,lim[α1(x)f(x)]存在,则
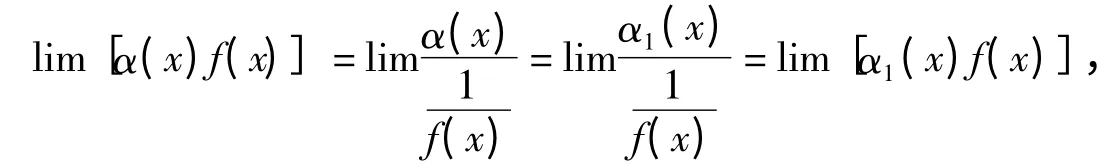
所以
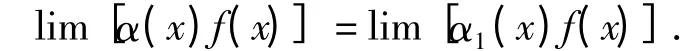
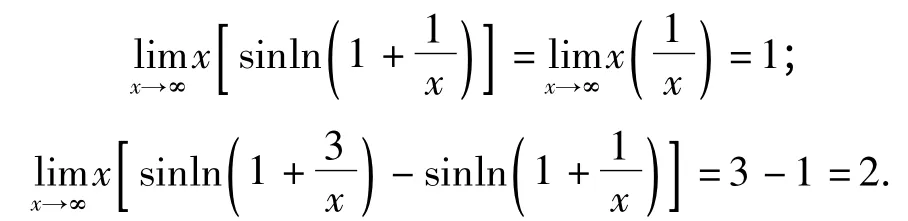
2 和差函数的等价无穷小代替
定理1 设α(x),α1(x),β(x),β1(x),ψ(x)是自变量在同一变化过程中的无穷小量,且α(x)~
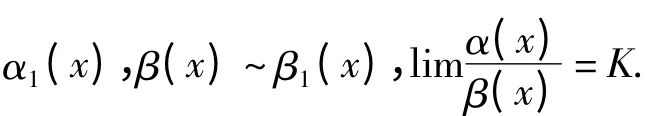
证明 (1)因为α(x),α1(x),β(x),β1(x)为无穷小量,由无穷小的性质有α(x)±β(x),α1(x)±β1(x),ψ(x)无穷小量,
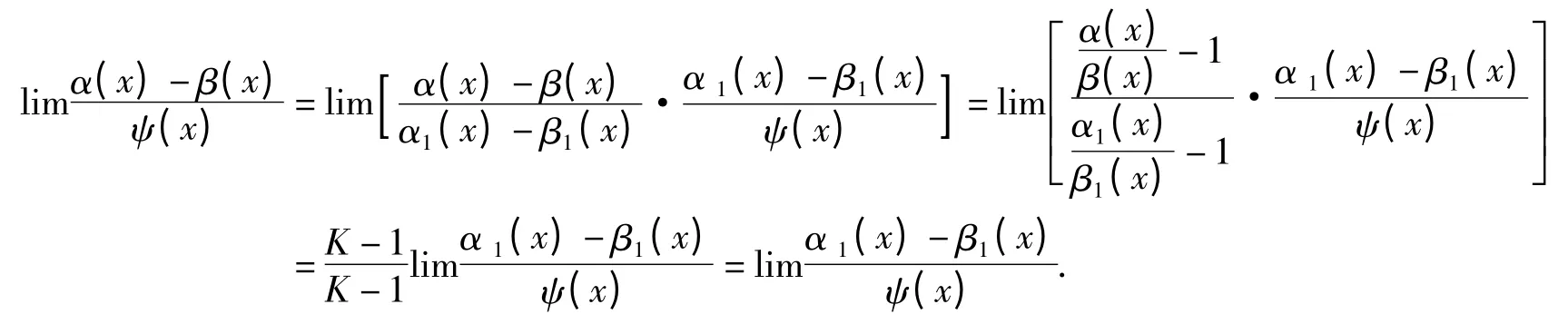
同理可证(2)
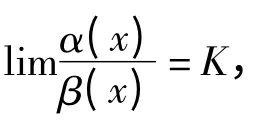
则 (1)若K≠1,α(x)-β(x)~α1(x)-β1(x);
(2)若K≠-1,α(x)+β(x)~α1(x)+β1(x).
例3 求
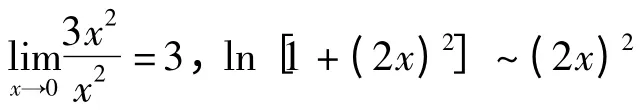
注意:若k= ±1 相关定理不成立。
成立于1992年的上海新星本是以制版设备起家,后于1997年将发展重点落于橡皮布。按照徐毛清的阐述,上海新星刚刚介入橡皮布这个市场时,国内已有七八家相关生产企业,但都规模较小,只能生产低档产品,因此中高端橡皮布市场被国外企业垄断。于是,徐毛清带领的上海新星决定攻克中高档市场,并暗下决心,“要做,就做高质量产品,做国内的老大“。
3 对数函数中的等价无穷小代替
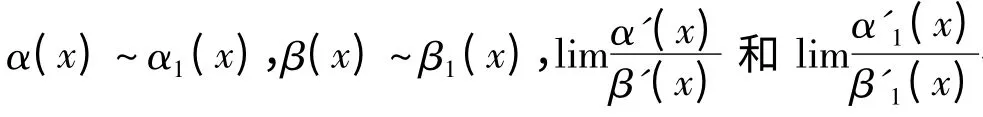
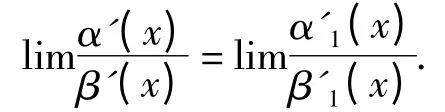
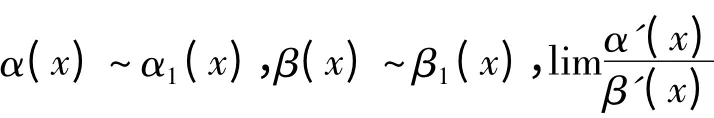
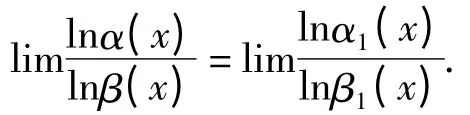
证明 由洛必达法则有
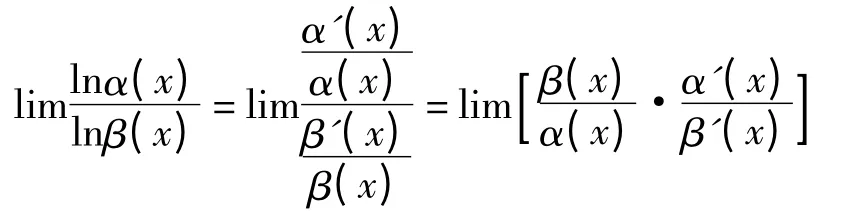
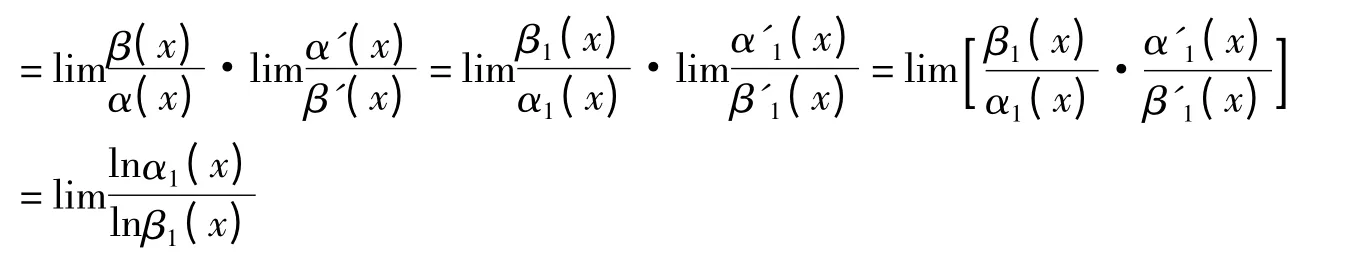
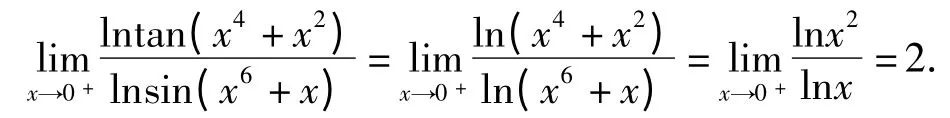
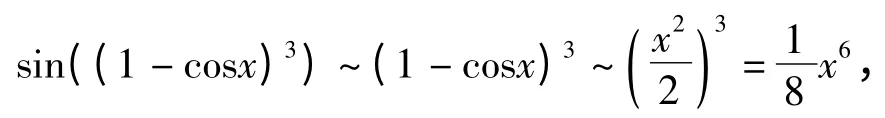
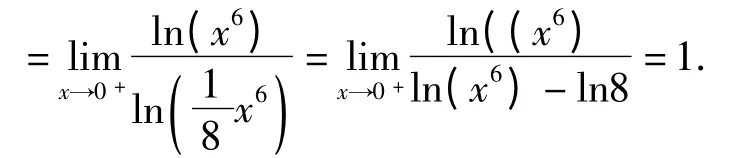
4 结语
在极限求解过程中,对于和差函数、乘积函数以及对数函数中的无穷小量适当利用等价无穷小代替,把复杂的无穷小变成简单的无穷小,起到了化繁为简的作用.
[1] 曹瑞成,姜海勤.大学数学[M].苏州:苏州大学出版社,2011.
[2] 同济大学应用数学系.高等数学[M].北京:高等教育出版社,2002.
[3] 伍华健.在求函数极限过程中使用等价无穷小[J].广西师院学报:自然科学版,1999(6):54 -56.
