冻融循环作用下泥质白云岩力学特性及损伤演化规律研究
2014-01-20吴安杰邓建华
吴安杰,邓建华,顾 乡,洪 彧
(1.西南交通大学 土木工程学院,成都 610031;2.贵州大学 土木建筑工程学院,贵阳 550003)
1 引 言
贵州是一个多山的省份,山地占全省面积绝大部分且气候多雨潮湿,低温凝冻天气出现频繁。泥质白云岩在该地区分布广泛,在基坑、边坡、隧道等开挖施工过程中使大量原先处于地下的岩石暴露出来置于复杂的气候环境中。受冻融环境的影响,岩石的力学性质将发生变化,这种变化往往会造成重大的灾害事故,因此,研究冻融循环条件下岩石的力学响应和变化机制对工程的设计、施工及安全运行具有重大意义。
岩石材料不同于一般的固体介质,它具有岩体本身的特殊的力学性质,受水作用影响很大[1-8],就岩石冻融循环问题国内外学者进行了一些研究[9-21],但涉及的岩石类型较少,且研究手段也较单一。虽然损伤力学的出现和发展对岩石力学性质、破坏机制的研究开辟了新思路,但到目前为止,仍没有找到一种较普遍适用的岩石本构关系模型。建立以冻融循环次数和应变为控制变量的本构模型很少[18-19],对于压缩状态下的曲线斜率递增的现象,文献[22]有所反映,但未明确提出斜率增大趋势系数这一概念。
本研究针对贵州常见的泥质白云岩借助于室内快速冻融循环试验和单轴压缩试验手段,分析研究了岩石在冻融后的力学性质变化规律,首次提出了斜率增大趋势系数的概念,即损伤修正因子。该系数的引入能形象地反映出岩石损伤存在的内涵,进一步理解损伤的本质,并建立了以冻融循环次数和应变为控制变量的本构模型,对冻融环境下的同类岩土工程设计和监测有重要意义。
2 试验过程
2.1 试样制作
泥质白云岩采自贵州地区某边坡处,通过现场钻芯取样、室内切割、打磨等工序,将同一批新鲜岩块加工成50 mm×100 mm(直径×高度)的圆柱体标准试样。借助RS-ST01C 非金属超声波检测仪(声时测量精度为0.1 μs)进行岩样纵波波速测定,按波速相近的原则选出岩样,确保岩样初始状态相同和减少试验数据的离散性。
2.2 室内快速冻融循环试验
将制作好的岩样采用自由浸水48 h 饱和,饱和后的试样分为7 组,每组5个岩样,放置在BCD-218C 低温数控恒温箱中,在-(20 ± 2)℃温度下冻12 h,然后取出浸泡在水槽中,水温保持在(20 ±2)℃,融化12 h,即每个冻融循环周期为24 h(目的是模拟天然环境冻融周期),共进行了30 次循环。
2.3 单轴压缩试验
将每隔5 次循环后的一组试样分别进行单轴压缩试验,单轴压缩试验设备为WDW3100 型微机控制电子万能试验机,最大试验力为100 kN,测量范围0.4% F.S.~100%F.S.,精度为±0.5%,调速范围为0.005~500 mm/min,位移分辨率为0.001 mm。试验加载速率为0.1 mm/min,径向变形采用千分表控制,具体操作按文献[23]要求进行。
3 试验结果及其分析
单轴压缩试验结果数据见表1(以每组岩样的平均值为代表值)。从试验压力机设备系统上可以直接获得单轴压缩状态下压力-位移全过程曲线及文档数据,经处理可得应力-应变全过程曲线、峰值应力(抗压强度)、峰值应变等参数。采用曲线峰前近似直线段(第3 阶段)进行线性拟合,并计算出弹性模量和泊松比。
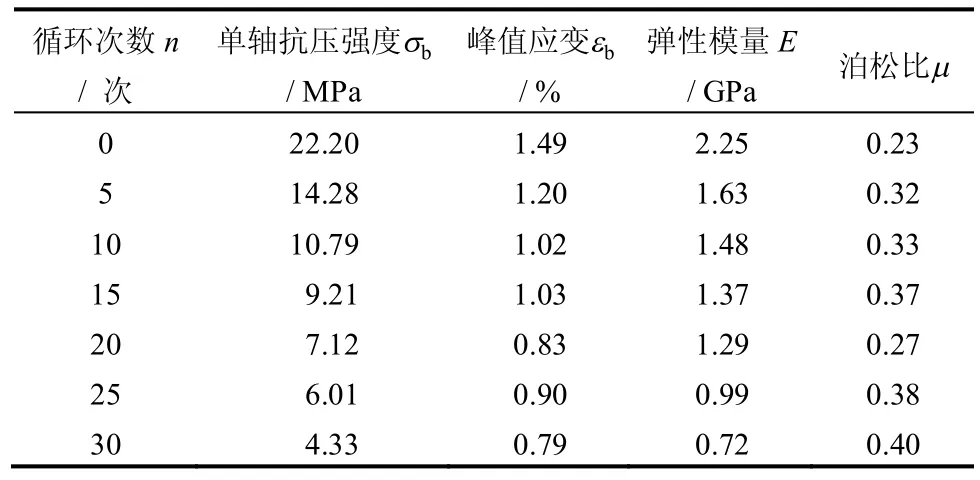
表1 泥质白云岩单轴压缩试验结果Table1 Results of uniaxial compressive testing of argillaceous dolomite under different freeze-thaw cycles
(1)应力-应变曲线
饱水的泥质白云岩试样经历不同冻融循环次数后单轴压缩状态下的应力-应变关系曲线如图1所示(为了使图片更清楚,每组选取了一条典型曲线)。

图1 泥质白云岩经历不同冻融次数后在单轴压缩状态下的应力-应变曲线Fig.1 Stress-strain curves for argillaceous dolomite under uniaxial compression and different freezing-thawing cycles
由图1 可以看出,随着冻融次数的增加,泥质白云岩的应力和应变峰值都有所降低,单轴压缩下应力-应变全过程曲线变化规律大致可以划分为5个阶段(以冻融20 次循环的典型曲线用字母标记)。
第1 阶段:AB 曲线形状呈上凹形,为2 次抛物线或多次幂函数,曲线斜率(切线弹性模量)逐渐增大,此时岩石中的初始微裂缝或微孔隙,在压力的作用下逐渐完成闭合密实,称为压密阶段。
第2 阶段:BC 曲线出现短暂的线形平缓期,此时应力增加缓慢,而应变速度陡增,岩石表现出局部滑移现象。曲线斜率降低,逐渐向稳定的线弹性阶段过渡。
第3 阶段:CD 曲线形状大致呈直线,斜率保持稳定,称为线弹性阶段。
第4 阶段:DE 曲线斜率变小,应力上升速度放缓,变形增速,逐渐濒临极限破坏。
第5 阶段:EF 当达到峰值应力后,应力迅速下降,出现应力跌落现象,而后应力出现缓慢下降,具有残余强度。曲线的下降段可统称为破坏阶段。
冻融循环对泥质白云岩性质的影响主要表现在第2、4、5 阶段。在冻融0 次时,即岩石未受冻融,此时曲线未出现第2 阶段或不明显,但该岩石经冻融循环后,出现第2 阶段,随后越来越明显。虽然此阶段短暂,但岩石表现出局部滑移现象,极易触发工程事故,须引起人们的重视。
由试验结果可知,随着冻融循环地进行,应力-应变曲线在第4 阶段变得越来越平缓,具有峰前塑性硬化行为特征。曲线下降段表现出峰后应变软化行为特征,在冻融的起初几个周期应力跌落比较明显,岩石表现为脆性破坏;随着损伤演变,曲线下降渐平缓,破坏形态向延性转化,由应力-应变曲线变化趋势可知,临界循环次数为18 次。
(2)峰值应力
泥质白云岩在单轴压缩峰值下的应力(抗压强度)随冻融循环次数增加的关系曲线如图2 所示。由图可见,冻融循环后,泥质白云岩的峰值应力参数值有所降低。在前10 次冻融循环,速度降低较快,后期变得缓慢些,呈指数下降趋势。经历30 次冻融循环时抗压强度降低了80%,冻融循环对该岩石损伤劣化明显。
峰值应力随冻融循环次数的拟合曲线方程为
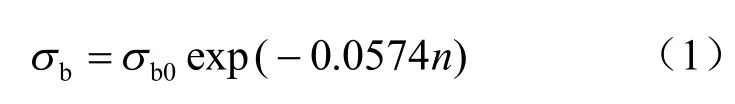
式中:σb为峰值应力;n为冻融循环次数。(3)峰值应变
泥质白云岩在单轴压缩状态下的峰值应变随冻融循环次数增加的关系如图3 所示。为了使曲线拟合更好,取每组试样的平均值为其特征代表值。峰值应变随着冻融循环次数的增加而降低,呈指数下降趋势。
峰值应变随冻融循环次数的拟合曲线方程为

式中:εb为峰值应变。
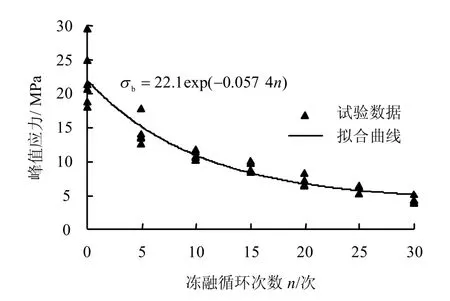
图2 泥质白云岩在单轴压缩状态下的峰值应力与冻融循环次数的关系曲线Fig.2 Relation curves between uniaxial compressive peak stress and freezing-thawing cycles for argillaceous dolomite
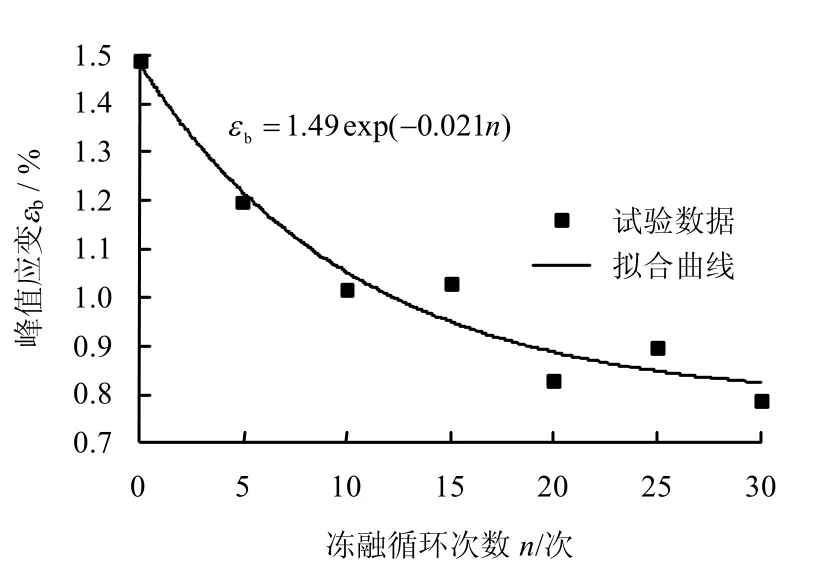
图3 泥质白云岩在单轴压缩下的峰值应变-冻融循环次数的关系曲线Fig.3 Relation curves between uniaxial compressive peak strain and freezing-thawing cycles for argillaceous dolomite
(4)弹性模量
泥质白云岩在单轴压缩下的弹性模量随冻融循环次数增加的关系如图4 所示。
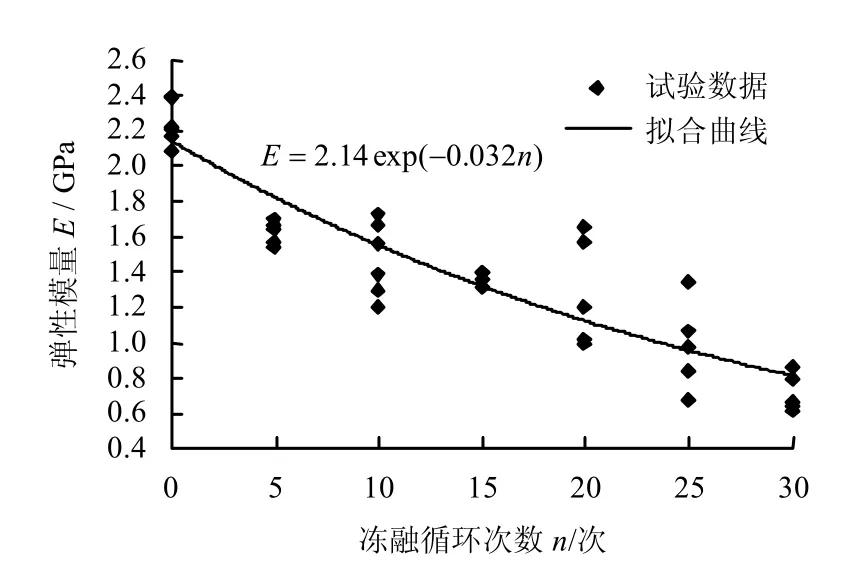
图4 泥质白云岩在单轴压缩下的弹性模量-冻融循环次数的关系曲线Fig.4 Relation curves between uniaxial compressive elastic modulus and freezing-thawing cycles for argillaceous dolomite
由图4 可见,冻融循环后泥质白云岩的弹性模量有所降低,前10 次冻融循环速度降低较快,后期变得缓慢些,呈指数下降趋势。
弹性模量随冻融循环次数的拟合曲线方程为
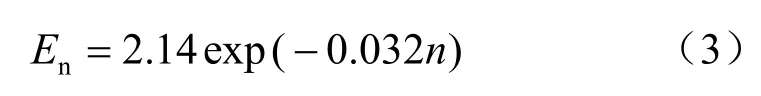
式中:En为弹性模量。
(5)泊松比
在单轴压缩试验中,泥质白云岩泊松比数据比较离散,笔者根据每组数据的离散程度,剔除每组中个别偏离较大的数据(数值与均值之比大于25%),用每组平均值作为特征代表值,拟合曲线图如图5 所示。

图5 泥质白云岩在单轴压缩下的泊松比-冻融循环次数的关系曲线Fig.5 Relation curve between uniaxial compressive Poisson’s ratio and freezing-thawing cycles for argillaceous dolomite
由图5 可见,冻融循环后泥质白云岩的泊松比近似呈线性增加变化。
泊松比随冻融循环次数的拟合曲线方程为
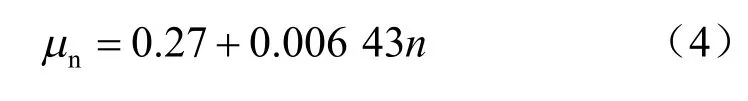
式中:μn为泊松比。
冻融后,个别岩样的泊松比值大于了0.50。分析原因:岩石受冻融损伤后,内部微孔隙出现或增大,相邻微粒之间的距离相比岩样的尺寸不再那么小,这时岩样不再是连续介质,或是连续性假定将引起显著的误差,结果岩样体应变为负,出现泊松比大于0.50 的现象。另一方面可能是受试验条件的影响,岩石径向变形不均匀,局部很大,取值限于千分表的两个对接点。
4 损伤演化规律
2003年,张全胜等[24]提出了基准损伤、正损伤、负损伤的概念,即材料的初始损伤状态定义为基准损伤状态,相应地将材料在受到荷载、冻融等作用而造成的微裂纹、微孔洞的扩展称为正损伤,同理把材料微裂纹、微孔洞的闭合称为负损伤。基于上述概念,张胜全将Lemaitre 应变等价原理[25]进行了推广,得出推广后的普遍应变等价原理,从而导出推广后的应力-应变损伤方程为
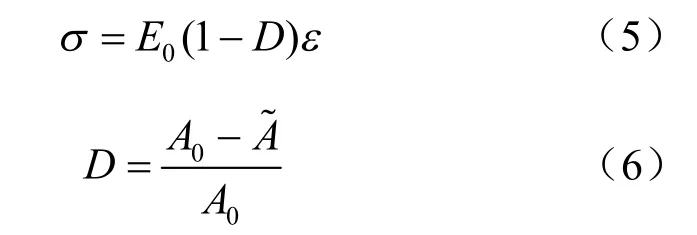
式中:A0、分别为材料基准损伤状态下的有效面积、正损伤或负损伤状态下的有效面积;E0为材料基准损伤状态下的弹性模量;σ、ε 分别为全应力、应变。
4.1 建立损伤演化方程和本构关系
图6为泥质白云岩经冻融后在单轴压缩下的一条典型应力-应变曲线(试样编号5-2)。由图中可知,随着压力的施加,曲线OA 的斜率越来越大,此时岩石中的初始微裂缝或微孔隙逐渐闭合密实。压力较小时,大的缝隙闭合;压力增大时,更大尺寸和更多数目的缝隙闭合,这就是所谓的负损伤过程,岩石变得更加密实,在到达A 点时,曲线的斜率按理说会继续增大,沿着假想的AN 趋势发展,然而正是由于岩石受到损伤作用缘故,应力减小,而应变增速,切线模量降低,局部出现塑性应变,真实曲线按照损伤的试验曲线进行,进入正损伤过程。
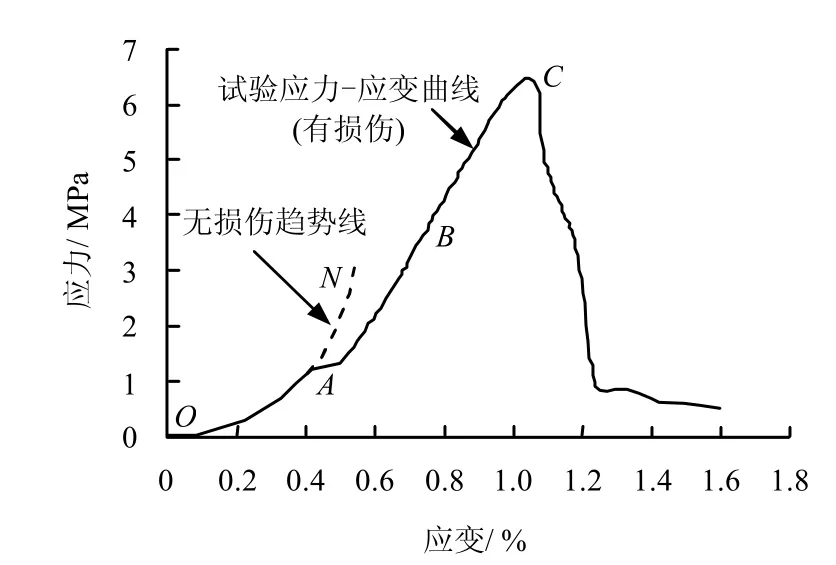
图6 泥质白云岩经冻融后在单轴压缩下的典型应力-应变曲线Fig.6 Typical stress-strain curve under uniaxial compression after freezing-thawing cycles for argillaceous dolomite
对式(5)求导:
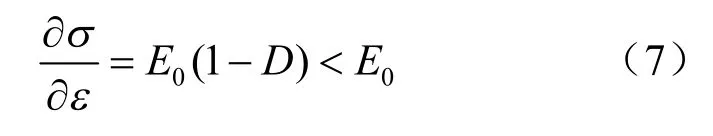
从式(7)可以看出,式(5)建立的应力-应变曲线关系没有反映出岩石曲线斜率增大的趋势。基于此,笔者引入斜率增大趋势系数i,即损伤修正因子,i 与岩石特性有关,可由曲线压密阶段OA的形状函数求导确定。此系数能更好地揭示有初始损伤岩石的损伤内涵,可得
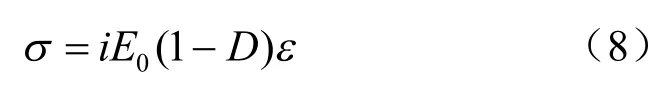
由于岩石材料内部构造极不均匀,各微元所具有的强度都不相同,考虑到岩石损伤是一个连续过程,各微元强度服从Weibull 分布,且定义损伤变量D为岩石中已经破坏的微元数目与总微元数目之比,可得

式中:m为形状参数;f为尺度参数,m>0,f>0。
将式(9)代入式(8),可得
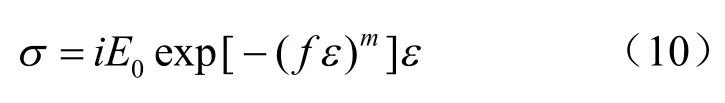
根据应力-应变关系曲线,有几何边界条件:
当ε=0时,

当ε=εb时,

当ε=∞时,

根据压密阶段曲线形状函数,为简单起见,可假设为2 次抛物线,则认为在无损伤的条件下应力-应变曲线斜率呈线性增加趋势,则令斜率增大系数:

式中:a为几何形状系数,a>0。
将式(9)、(10)、(14),结合边界条件式(11)~(13)整理推导可得

式中:

式(15)、(16)分别为考虑斜率增大趋势系数的损伤演化方程和本构模型;系数m为形状系数,a为几何形状系数,两者之间存在数学表达的关系(同前),都是表征该岩石损伤行为的固有属性。
将式(1)、(2)代入式(16)中,可得以冻融循环次数和应变为控制变量的损伤本构模型,即

由冻融前泥质白云岩单轴压缩下应力-应变曲线在压密阶段(负损伤阶段)的曲线形状可知,可取几何形状系数a=4.5。
基于宏观角度,用弹性模量作为损伤因子的损伤规律。定义损伤变量:

由推广后的应变等效原理[18],将式(3)代入式(19),可以推出仅含冻融循环次数n为变量的损伤演化方程,即
4.2 损伤特性分析
基于数据量大,采用大型数学、图形处理软件Maple,根据式(20)与式(18)可以作出泥质白云岩冻融损伤特性曲线与本构关系曲线,如图7、8所示。
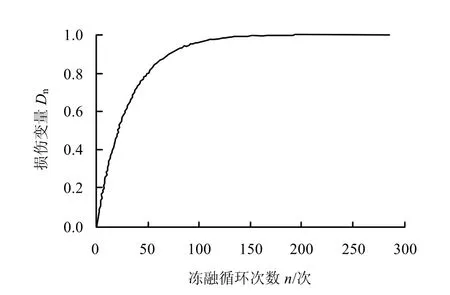
图7 泥质白云岩冻融损伤演化特性曲线Fig.7 Evolution curve of damage properties with freezing-thawing cycles for argillaceous dolomite
由图7 可见,随着冻融循环次数的增加,冻融损伤值在增大,冻融循环前期(0~20 次),损伤速度较快(损伤值从0 变到0.35);在冻融循环中期(20~50 次)损伤速度略有减缓,到30 次循环时,损伤值达到0.72;冻融循环后期,损伤逐渐缓和,接近150 次循环时,损伤值变为1,则岩样成理想状态下的完全损伤。
从试验结果来看,当冻融循环至30 次时,岩样出现各种形态的裂缝,主要是环向裂缝、纵向裂缝、斜裂缝,多条裂缝交织,岩样颗粒松散,出现不同程度的剥落现象;冻融循环过程中,抗压强度、峰值应变、弹性模量多个力学参数值降低,经历30次冻融循环时,抗压强度降低了80%,此时岩样损伤严重,损伤值已达到0.72,说明冻融环境造成岩样内部结构损伤劣化程度为72%,损伤劣化明显。笔者仅进行了30 次冻融循环,可以达到了解岩石损伤过程的试验目的。
由图8 可以看出,泥质白云岩在单轴压缩下应力、应变峰值随着冻融循环次数的增加而降低;曲线下降段变得越来越平缓,在冻融的起初几个周期,岩石表现为脆性破坏,随着损伤演变,岩石的延性有所增强,临界次数为18,即脆性向延性转变的门槛值。上述与试验结果分析是一致的,说明建立的理论本构模型是合理的。
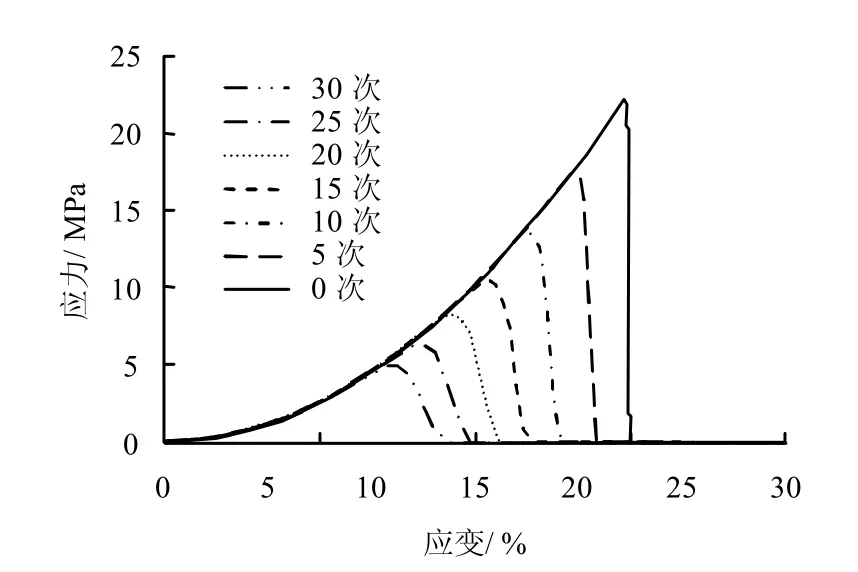
图8 泥质白云岩经不同冻融次数后单轴压缩下的本构关系曲线Fig.8 Constitutive relation curves under uniaxial compression after different freezing-thawing cycles for argillaceous dolomite
图9为泥质白云岩试样在冻融循环10 次时的理论本构关系曲线与试验应力-应变曲线。理论本构关系曲线与真实的试验应力-应变曲线基本吻合,说明笔者建立本构模型时引入的斜率增大趋势系数i,并考虑为线性增加趋势是正确的和可行的。
值得注意的是,理论本构关系曲线弱化了曲线的第2 阶段,即线形平缓段,真实的试验曲线表现很明显,此理论本构模型不适用于三轴压缩的情况。三轴压缩存在围压的影响,情况会更复杂,需要进一步深入地研究。
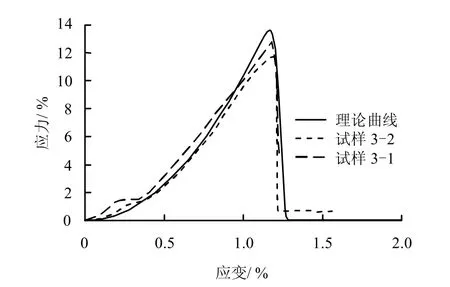
图9 泥质白云岩在冻融循环10 次时理论本构关系曲线与单轴压缩试验应力-应变曲线Fig.9 Theory constitutive curves vs.stress-strain curves under uniaxial compression in 10th freezing-thawing cycles for argillaceous dolomite
5 结 论
(1)冻融循环对泥质白云岩的力学性质影响很大,随着冻融次数的增加,岩石单轴抗压强度、峰值应变、弹性模量等多个力学参数呈指数下降,而泊松比呈线性增加变化。经历30 次冻融循环时,抗压强度降低了80%,损伤值已达到0.72;当冻融循环150 次时,损伤值为1,则岩样成理想状态下的完全损伤,强度丧失。相对循环后期,前期损伤劣化速度较快,结果表明冻融循环对泥质白云岩内部结构损伤劣化明显。
(2)在单轴压缩状态下,泥质白云岩应力-应变全过程曲线具有峰前塑性硬化和峰后应变软化等行为特征。受冻融循环影响,在第1 阶段后出现短暂的线形平缓阶段,具有岩石局部滑移现象,须引起从事寒区类似岩土工程设计与施工人员的重视,以避免灾害事故。随着冻融循环的进行,岩石破坏形态从脆性向延性转化,临界周期值为18。
(3)理论本构模型与试验结果相符合,说明引入斜率增大趋势系数,并考虑为线性增加,是合理和可行的。值得注意的是,理论本构关系曲线弱化了第2 阶段,即线形平缓阶段。
借助室内快速冻融循环试验和单轴压缩试验,可以比较直接有效地研究岩石材料受低温凝冻极端气候影响后的损伤特性。
[1]HAWKINS A B,MCCONNELL B J.Sensitivity of sandstone strength and deformability to changes in moisture content[J].Quarterly Journal of Engineering Geology,1992,25:115-130.
[2]OJO O.The effect of moisture on some mechanical properties of rock[J].Mining Science and Technology,1990,10:145-157.
[3]邓建华,黄醒春,彭结兵,等.膏溶角砾岩不同天然含水率情况下力学特性的试验研究[J].岩土工程学报,2008,30(8):1203-1207.DENG Jian-hua,HUANG Xing-chun,PENG Jie-bing,et al.Mechanical properties of gypsum breccia with different water contents[J].Chinese Journal of Geotechnical Engineering,2008,30(8):1203-1207.
[4]LAZHAR B,LOTFI M,AMMAR T.Water-rock interaction and geochemistry of groundwater from the Ain Azeaquiter,Algeria[J].Environmental Geochemistry and Health,2009,28(10):1995-2005.
[5]ABDELGAWAD M,WATANABE K,TAKEUCHI S.Water-rock interaction study on the occurrence of fluoride-rich groundwater at Miaunamiarea:Area,Japan[J].Environment Asia,2009,2:20-29.
[6]ERGULER Z A,ULUSAY R.Water-induced variations in mechanical properties of clay-bearing rocks[J].International Journal of Rock Mechanics and Mining Sciences,2009,46:355-370.
[7]陈瑜,曹平,蒲成志,等.水-岩作用对岩石表面微观形貌影响的试验研究[J].岩土力学,2010,31(11):3452-3458.CHEN Yu,CAO Ping,PU Cheng-zhi,et al.Experimental study of effect of water-rock interaction on mictotopography of rock surface[J].Rock and Soil Mechanics,2010,31(11):3452-3458.
[8]MIRONENKO M V,ZOLOTOV M Y.Equilibriumkinetic model of water-rock interaction[J].Geochemistry International,2012,50(1):1-7.
[9]HORI M,MORIHIRO H.Micromechanical analysis of deterioration due to freezing and thawing in porous brittle materials[J].International Journal of Rock Mechanics and Mining Sciences,1998,36(4):511-522.
[10]RUIZE D E,ARGANDONA V G,RODRIGUEZ R A,et al.Characterization by computed X-ray tomography of the evolution of the pore structure of a dolomite rock during freeze-thaw cyclic tests[J].Phys.Chem.Earth,1999,24(7):633-637.
[11]IÑGO A C,VICENTE M A,RIVES V.Weathering and decay of granitic rocks:Its relation to their pore network[J].Mechanics of Materials,2000,32:555-560.
[12]杨更社,蒲毅彬,马魏.寒区冻融循环环境条件下岩石损伤扩展研究探讨[J].实验力学,2002,17(2):220-226.YANG Geng-she,PU Yi-bing,MA Wei.Discussion on the damage propagation for the rock under the frost and thaw condition frigid zone[J].Journal of Experimental Mechanics,2002,17(2):220-226.
[13]MUTLUTÜRK M,ALTINDAG R,TÜRK G.A decay function model for the integrity loss of rock when subjected to recurrent cycles of freezing-thawing and heating-cooling[J].International Journal of Rock Mechanics &Mining Sciences,2004,41:237-244.
[14]ZHANG S J,LAI Y M,ZHANG X F,et al.Study on the damage propagation of surrounding rock from a cold-region tunnel under freeze-thaw cycle condition[J].Tunnelling and Underground Space Technology,2004,19(3):295-302.
[15]何国梁,张磊,吴刚.循环冻融条件下岩石物理特性的试验研究[J].岩土力学,2004,25(2):52-56.HE Guo-liang,ZHANG Lei,WU Gang.Test study on physical characteristics of rock under freezing-thawing cycles[J].Rock and Soil Mechanics,2004,25(2):52-56.
[16]KUBICAR L,VRETENAR V,BOBAC V,et al.Thermophysical analysis of sandstone by pulse transient method[J].International Journal of Thermophysics,2006,27(1):220-234.
[17]林战举,牛富俊,刘华.循环冻融对冻土路基护坡块石物理力学特性的影响[J].岩土力学,2011,32(5):1369-1376.LIN Zhan-ju,NIU Fu-jun,LIU Hua.Influences of freezing-thawing cycles on physico-mechanical properties of embankment revetments in permafrost regions[J].Rock and Soil Mechanics,2011,32(5):1369-1376.
[18]张慧梅,杨更社.岩石冻融力学实验及损伤扩展特性[J].中国矿业大学学报,2011,40(1):140-145.ZHANG Hui-mei,YANG Geng-she.Freeze-thaw cycling and mechanical experiment and damage propagation characteristics of rock[J].Journal of China University of Mining and Technology,2011,40(1):140-145.
[19]张慧梅,杨更社.冻融荷载耦合作用下岩石损伤力学特性[J].工程力学,2011,28(5):161-165.ZHANG Hui-mei,YANG Geng-she.Damage mechanical characteristics of rock under freeze-thaw and load coupling[J].Engineering Mechanics,2011,28(5):161-165.
[20]李杰林,周科平,张亚民.基于核磁共振技术的岩石孔隙结构冻融损伤试验研究[J].岩石力学与工程学报,2012,31(6):1208-1214.LI Jie-lin,ZHOU Ke-ping,ZHANG Ya-min.Experimental study of rock porous structure damage characteristics under condition of freezing-thawing cycles based on nuclear magnetic resonance technique[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(6):1208-1214.
[21]DEMIRDAG S.Effects of freezing-thawing and thermalshock cycles on physical and mechanical properties of filled and unfilled travertines[J].Construction and Building Materials,2013,47:1395-1401.
[22]秦跃平.岩石损伤力学模型及本构方程的探讨[J].岩石力学与工程学报,2001,20(4):560-562.QIN Yue-ping.Discussion on damage mechanics and constitutive equation of rock[J].Chinese Journal of Rock Mechanics and Engineering,2001,20(4):560-562.
[23]长江水利委员会长江科学院.SL264-2001 水利水电工程岩石试验规程[S].北京:中国水利水电出版社,2001.
[24]张全胜,杨更社,任建喜.岩石损伤变量及本构方程的新探讨[J].岩石力学与工程学报,2003,22(1):31-34.ZHANG Quan-sheng,YANG Geng-she,REN Jian-xi.New study of damage variable and constitutive equation of rock[J].Chinese Journal of Rock mechanics and Engineering,2003,22(1):31-34.
[25]LEMAITRE J.How to use damage mechanics[J].Nuclear Engineering and Design,1984,80(1):233-245.
