新鲜生活垃圾压缩与直剪联合测定试验研究
2014-01-20张振营严立俊吴大志
张振营,严立俊,吴大志
(浙江理工大学 建筑工程学院,杭州 310018)
1 引 言
生活垃圾由很多性质不同的成分组成,包括废纸、蔬菜、果皮、木、草、树叶、纺织品、肉骨、塑料、橡胶、金属、砖、石、土、陶瓷、玻璃等。这些成分通常是多孔和非饱和的,对生活垃圾的工程性质产生很大影响[1]。影响垃圾土强度的因素有很多,如有机质和纤维素含量、填埋时间、降解程度、压实方式、压实程度、组成成分、颗粒大小及含水率等[2-3]。一些学者对城市固体废弃物(MSW)的变形和强度特性进行了研究,Machado 等[4]把MSW 分成纤维状的加筋相和泥状物两部分,在分析室内三轴试验结果的基础上提出一个复合本构模型,纤维状的加筋相采用弹塑性模型,泥状物采用修正剑桥模型。Babu 等[5]认为,在荷载作用下修正剑桥模型被扩展,总应变包括两部分,即蠕变应变和降解应变。Diambra 等[6]基于混合物原则建立了加筋土本构模型,认为纤维相采用线弹性模型,基本相采用理想弹塑性模型。Jonathan 等[7]分析了MSW 的组成、侧限应力、有机物成分、加载速率等对抗剪强度的影响。Christopher 等[8]分析了MSW的组分和降解的不同对MSW 剪切强度的影响。张振营等[9]采用邓肯-张模型来表达MSW 的应力-应变关系。朱俊高等[10]采用直线拟合了垃圾的应力-应变关系曲线。张季如等[11]分别进行直剪试验和旁压试验测定生活垃圾的强度,得到了垃圾的应力-应变关系。冯世进[12]提出将多组分的MSW 看作一个整体,采用邓肯-张模型来模拟其应力-应变关系。孙秀丽等[13]采用双曲线模型来表达MSW 的应力-应变关系。陈继东等[14]针对垃圾填埋场沉降计算问题,考虑垃圾土中有机物降解及降解过程中重度的变化,推导了垃圾土一维压缩计算的修正公式。张文杰等[15]基于现场取样进行室内测试,对垃圾土重度和抗剪强度参数的变异规律和概率特性进行研究,采用蒙特卡罗法分析了填埋边坡可靠度。王伟等[16]对1~7 d 龄期内的垃圾进行了直剪试验,提出一个复合正切-指数模型来表达剪应力-剪切位移的关系。郭城等[17]用邓肯-张模型、修正剑桥模型模拟MSW 单元体的应力-应变关系,提出了弹塑性蠕变降解模型。王磊等[18]在加筋土模型的基础上进行适当修正,建立了包括基本相的修正剑桥模型和纤维相的线弹性模型。本文在总结他们各自研究成果的基础上,将生活垃圾材料分为易降解材料、难降解材料及不可压缩的固体材料三类,采用3种不同的初始孔隙比、4 种不同的竖向压力,每种压力按照8 种不同的压缩时间,进行了新鲜生活垃圾的压缩与直剪联合测定试验,系统地对城市新鲜生活垃圾在不同压缩应变下的强度特性进行了研究。
2 试验仪器及材料
试验采用大型固废压缩-直剪联合测定仪进行,仪器见图1。试验容器的内直径为180 mm,容器上下盒高150 mm,水平剪切位移量程为0~45 mm。仪器由竖向压力系统、竖向压缩测试系统、水平剪力系统及水平位移量测系统4 部分组成,其中水平剪力及水平位移数据可以自动采集。本次试验参照杭州天子岭固体废弃物填埋场垃圾的主要成分,人工配制试样,其湿质量比分别为50%、15%和35%,成分比例见表1。

图1 固体废弃物压缩-直剪联合测定仪Fig.1 Compression-direct shear combined test apparatus for municipal sold waste(MSW)

表1 新鲜生活垃圾的成分比例(湿重)Table 1 Percentage composition of fresh MSW(wet weight)
3 试验过程
按《土工试验规程》[19]进行压缩与直剪联合试验。
3.1 制样过程
采集新鲜生活垃圾,按表1 各成分的比例秤取并配制垃圾。采用相对比重瓶法[20]得到垃圾各成分的相对密度,再根据50%、15%及35%的配比计算出垃圾的加权平均相对密度。采用烘干法[20]测出垃圾的含水率,根据式(1)计算出垃圾的天然密度,并得到垃圾试样各成分的质量,将各成分混合并搅拌均匀,静置24 h,将垃圾倒入试验容器内,采用分层压实的方法,对MSW 进行压实,然后倒入垃圾、再压实并重复上述步骤,直到垃圾全部填满容器且被压实为止,同时保证垃圾试样的初始孔隙比分别为2.1、2.5、2.9,随后放置透水石和加压板,将百分表对准加压板的中心,调整百分表并记录初始读数。将剪切试验速率调整到1.8 mm/min,并做好试验前的一切准备工作。初始孔隙比为

式中:ds为试样的加权平均相对密度;ω为试样的含水率;ρ为试样的天然密度。
3.2 加压试验过程
竖向压力分别为25、50、100、200 kPa,每级压力作用的时间分别为0、0.25、0.5、1、2、6、12、24 h,某级压力作用下记录压缩时间,采用快剪的方式使试样剪切破坏。为便于说明,以初始孔隙比e=2.1,竖向压力25 kPa为例,对试验过程进行叙述。施加压力25 kPa,首先进行加压后的快剪试验,记录剪应力和剪切位移,直到MSW 试样破坏为止(要求剪切应变超过20%)。剪坏后,重新安装相同的试样,施加压力25 kPa,记录压缩时间并观测压缩量,压缩到0.25 h时,进行快剪试验,直到试样破坏为止(要求剪切应变超过20%)。剪坏后,按同样的方法依次分别安装相同的试样,施加荷载25 kPa,压缩时间依次为0.5、1、2、6、12、24 h,记录相应的压缩量,依次分别进行剪切试验,直到试样破坏为止(要求剪切应变超过20%)。然后再分别安装相同的垃圾试样,分别施加压力50、100、200 kPa,压缩时间分别为0、0.25、0.5、1、2、6、12、24 h,按同样的方法重复上述试验步骤,记录全部的试验数据。
4 试验结果及分析
4.1 不同压缩时间下剪应力与剪应变的关系
某级压力下压缩时间分别为0、0.25、0.5、1、2、6、12、24 h时的剪应力与剪应变的关系如图2所示。从图中可以看出,3 种不同初始孔隙比e0所得到的结论基本一致,即随着剪应变的增加,剪应力的总体趋势在增加,且增大的趋势有逐渐变缓的迹象是一条剪应变硬化曲线,符合双曲线模型。将纵坐标转化成γ/τ,如图3 所示。由图可见,γ/τ与γ 的关系可以拟合成一条直线,直线方程为

式中:a、b为与竖向压力、压缩时间、材料组分等因素有关的参数。根据试验数据得出参数a为0.028~0.144,参数b为0.012~0.024。
4.2 不同竖向压力及不同剪应变限值下抗剪强度与竖向压缩应变的关系
垃圾填埋过程中,随着新鲜垃圾的逐渐堆高,垃圾填埋体出现压缩变形并伴随滑移失稳的趋势。模拟垃圾填埋场中垃圾之间及防渗层与垃圾之间的相对位移,把剪应变限值定为5%、10%、15%、20%,其对应的剪应力即为抗剪强度。新鲜垃圾的fτ-εv关系如图4 所示。从图中可以看出,3 种不同孔隙比新鲜垃圾的τf-εv的规律基本相同,即在相同初始孔隙比及相同剪应变下,τf随着竖向压力的增大而增大;在相同初始孔隙比、竖向压力及剪应变下,τf随着压缩时间的延长而增大,但压缩时间超过6 h 后τf又减小,当压缩时间超过12 h 后τf又增大,且随着压力越大,规律越明显。分析原因,MSW 本身是由多种组分构成,随着压缩时间的延长,垃圾各组分重新排列,并趋于密实,抗剪强度随之增加,当压缩时间超过6 h 后,垃圾组成中的易降解、易压缩成分由于压缩原因,很多水分流出,对MSW 本身起到润滑作用,因而其抗剪强度开始降低,当压缩时间再延长时,水分流出,结构重新排列并趋于密实,抗剪强度随之又开始增加。在相同压缩时间、竖向应变和剪应变下,τf随着初始孔隙比的增加而减小。图4 中,实线部分为拟合曲线,方程可用式(3)表示,其规律与试验结果吻合得较好。其相关参数和拟合系数的参考值见表2。
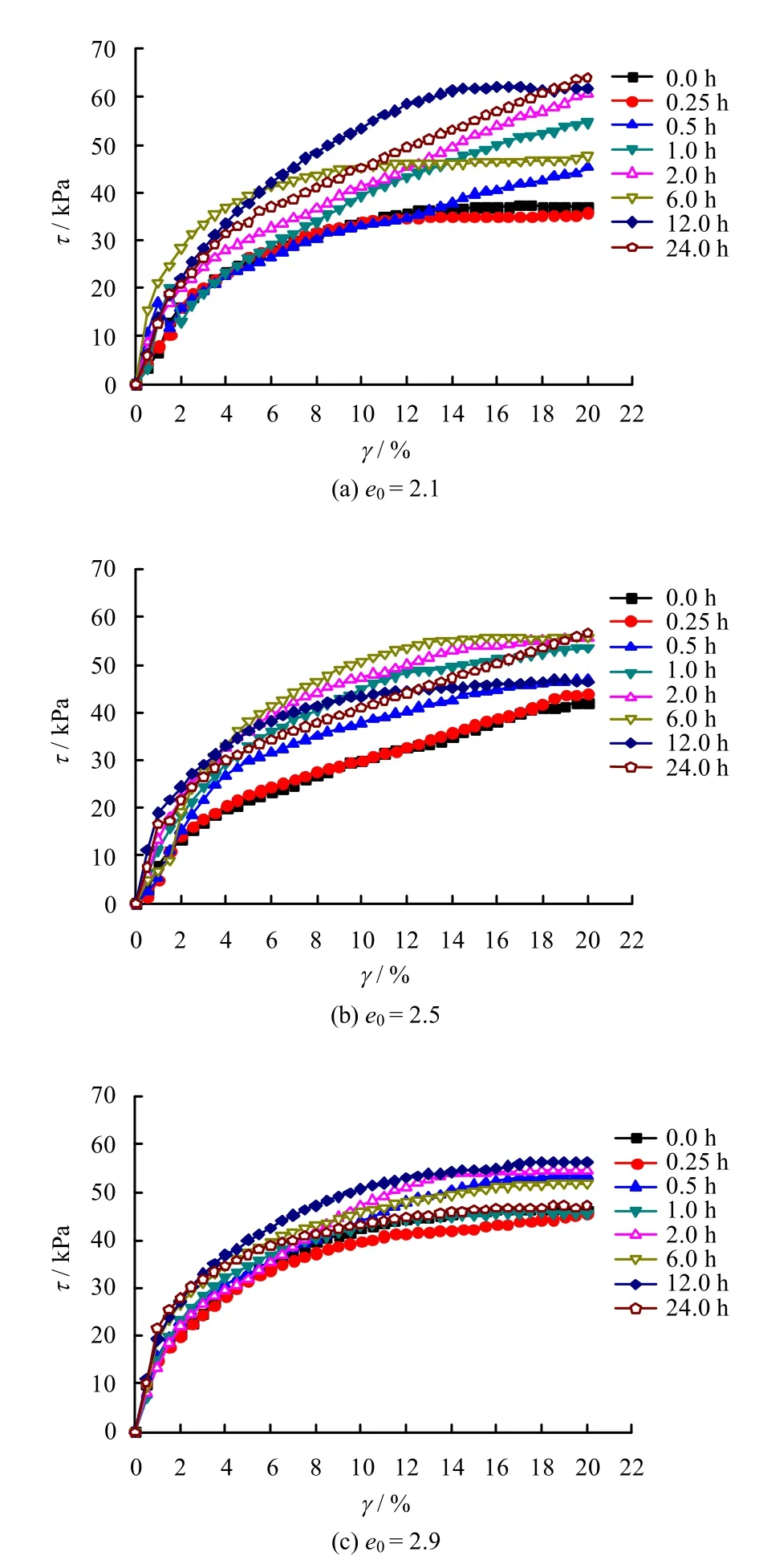
图2 不同压缩时间下MSW 的τ-γ 曲线Fig.2 τ-γ curves of MSW under different compression times
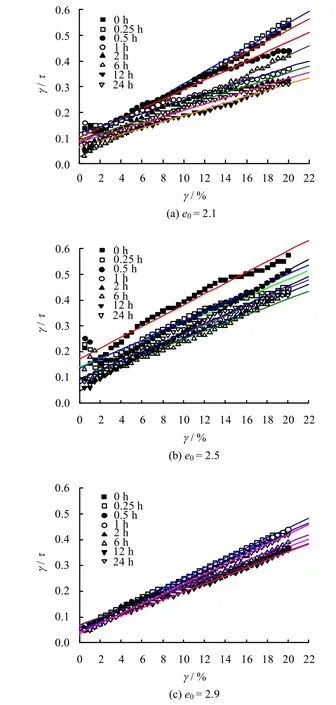
图3 不同压缩时间下MSW 的γ/τ-γ 曲线Fig.3 γ/τ-γ curves of MSW under different compression times

式中:A、B、C、D 分别为与初始孔隙比、组分、时间、竖向压力、剪应变等因素有关的系数。根据文献[21]有式(4)。
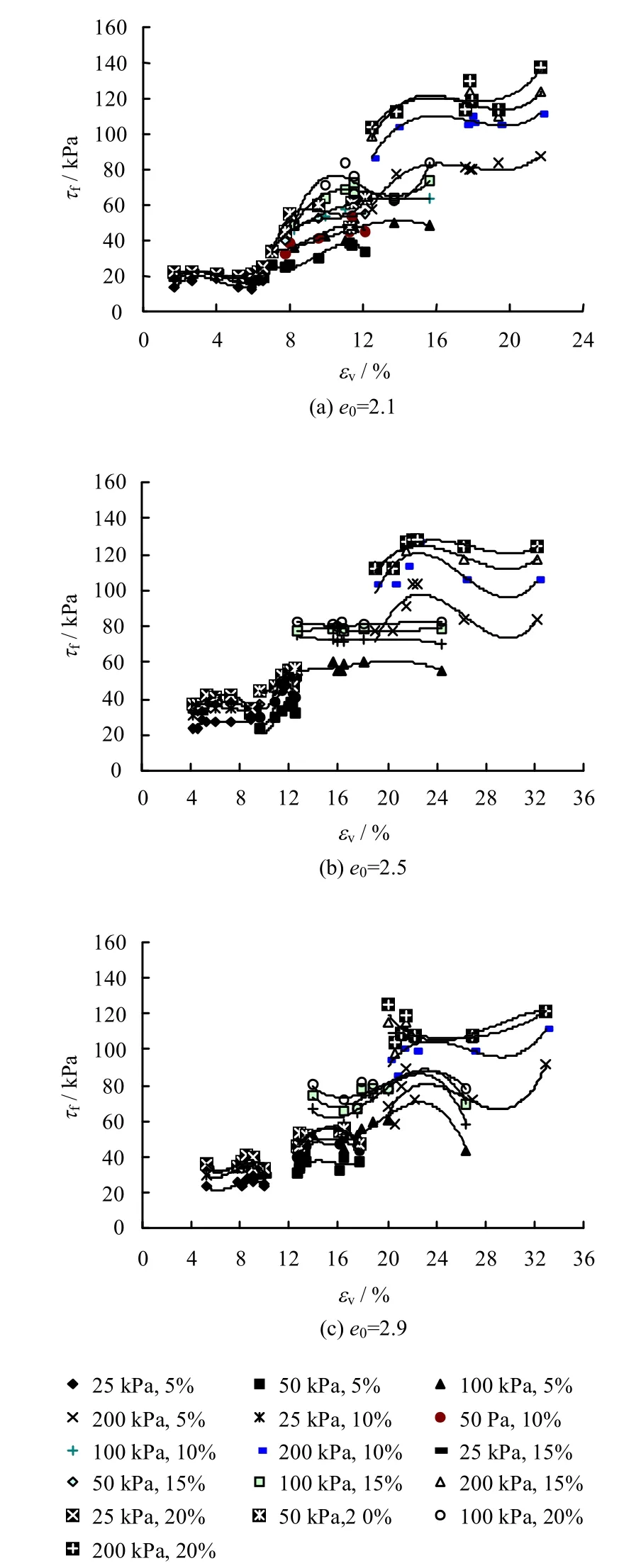
图4 不同初始孔隙比τf-εv曲线Fig.4 τf-εvcurves of MSW with different initial void ratios

式中:L、M 分别为与压力、初始孔隙比、材料组分等因素有关的参数。
将式(4)代入式(3)得出τf-t 关系,即
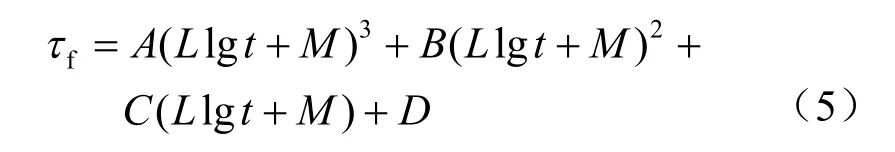
简化可得

式中:f、g、j、k 分别为与初始孔隙比、组分、时间、竖向压力、剪应变等因素有关的系数。
4.3 不同初始孔隙比的抗剪强度与竖向压力的关系
为便于说明,以压缩时间为0 h 和24 h为例,不同剪应变限值的τf-σ 关系曲线如图5 所示。由图可知,MSW 的τf-σ 关系符合库仑定律,MSW的抗剪强度随压力的增大而增大、随初始孔隙比的增加而减小、随剪应变的增大而增大。新鲜垃圾在压缩时间为0 h 和24 h 的抗剪强度参数见表3。由表可以看出,新鲜生活垃圾的黏聚力c 值在11.1~34.2 kPa 之间,内摩擦角φ 值在11.2°~30.6°之间。

表2 MSW 的拟合参数表Table 2 Fitted parameters of MSW
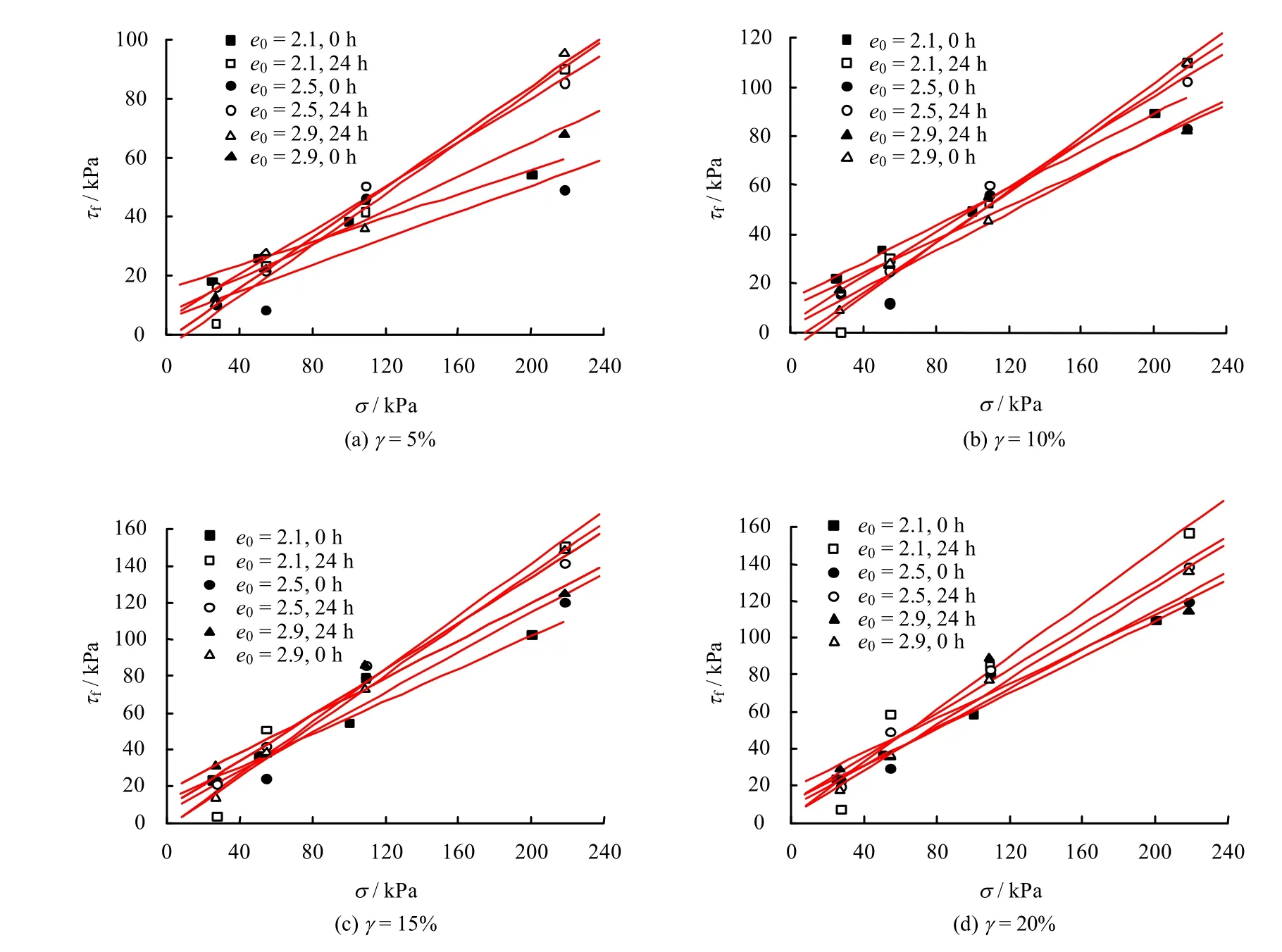
图5 MSW 的抗剪强度包线Fig.5 Shear strength envelope curves of MSW

表3 MSW 的抗剪强度参数Table 3 Shear strength parameters of MSW
5 结 论
(1)MSW 的剪应力随着剪应变的增大而增大,但其增大的趋势逐渐变缓。随着初始孔隙比的增加,其剪应力值减小。剪应力-剪应变的关系符合双曲线模型,得到了模型参数的取值范围,a 在0.028~0.144 之间,b 在0.012~0.024 之间。
(2)随着竖向应变(压缩时间)的增大,抗剪强度的值有先增大,后减小,然后再增大的趋势。根据试验数据,新鲜垃圾的强度-变形-时间的理论模型可以拟合成3 次多项式的形式,给出了τf与εv及τf与t 的关系表达式,并给出了参数的拟合值及相关系数的取值,相关系数在0.63~0.98 之间。
(3)新鲜生活垃圾不同压缩时间段的抗剪强度与竖向压力的关系符合库仑定律,试验得到了3 种初始孔隙比新鲜生活垃圾的黏聚力和内摩擦角的取值范围。黏聚力c 值在11.1~34.2 kPa 之间,内摩擦角φ 值在11.2°~30.6°之间。
本文没有考虑温度、降解等因素的影响。对于降解垃圾的长期压缩变形与强度的相关特性将另行撰文研究。
[1]钱学德,郭志平.城市固体废弃物(MSW)的工程性质[J].岩土工程学报,1998,20(5):1-6.QIAN Xue-de,GUO Zhi-ping.Engineering properties of municipal solid waste[J].Chinese Journal of Geotechnical Engineering,1998,20(5):1-6.
[2]孙秀丽.城市固体废弃物变形及强度特性研究[博士论文D].大连:大连理工大学,2007.
[3]周健,刘文白,贾敏才.环境岩土工程[M].北京:人民交通出版社,2004.
[4]MACHADO S L,CARVALLHO F M,VILAR O M.Constitutive model for municipal solid waste[J].Journal of Geotechnical and Geoenvironmental Engineering,2002,128(11):940-951.
[5]SIVAKUMAR B G L,REDDY K R,CHOUKSEY S K.Constitutive model for municipal solid waste incorporating mechanical creep and biodegradationinduced compression[J].Waste Management,2010,30(1):11-22.
[6]DIAMBRA A,IBRAIM E,MUIR W D,et al.Fiber reinforced sands:Experiments and modeling[J].Geotextiles and Geomembrances,2010,28(3):238-250.
[7]BRAY J D,ZEKKOS D,KAVAZANJIAN J E,et al.Shear strength of municipal solid waste[J].Journal of Geotechnical and Geoenvironmental Engineering,ASCE,2009,135(6):709-722.
[8]BAREITHER C A,BENSON C H,EDIL T B.Effects of waste composition and decomposition on the shear strength of municipal solid waste[J].Journal of Geotechnical and Geoenvironmental Engineering,ASCE,2012,138(10):1161-1174.
[9]张振营,吴世明,陈云敏.城市生活垃圾土性参数的室内试验研究[J].岩土工程学报,2000,22(1):35-39.ZHANG Zhen-ying,WU Shi-ming,CHEN Yun-min.Experimental research on the parameter of life rubbish in city[J].Chinese Journal of Geotechnical Engineering,2000,22(1):35-39.
[10]朱俊高,施建勇.垃圾填埋场固体废弃物的强度特性试验研究[C]//第一届全国环境岩土工程与土工合成材料技术研讨会论文集.杭州:浙江大学出版社,2002.
[11]张季如,陈超敏.城市生活垃圾抗剪强度参数的测试与分析[J].岩石力学与工程学报,2003,22(1):110-114.ZHANG Ji-ru, CHEN Chao-min.Measurement and analysis of shear strength parameters of municipal solid waste[J].Chinese Journal of Rock Mechanics and Engineering,2003,22(1):110-114.
[12]冯世进.城市固体废弃物静动力强度特性及填埋场的稳定性分析[博士论文D].杭州:浙江大学,2005:69-92.
[13]孙秀丽,孔宪京,邹德高,等.城市固体废弃物应力-应变模型研究[J].岩土工程学报,2008,30(5):726-731.SUN Xiu-li,KONG Xian-jing,ZOU De-gao,et al.Stress-strain model for municipal solid waste[J].Chinese Journal of Geotechnical Engineering,2008,30(5):726-731.
[14]陈继东,施建勇,胡亚东.垃圾土一维压缩修正公式及有机物降解验证试验研究[J].岩土力学,2008,29(7):1797-1801.CHEN Ji-dong,SHI Jian-yong,HU Ya-dong.Onedimensional compression modified method of settlement of landfills and verification of degradation of organic content in solid waste[J].Rock and Soil Mechanics,2008,29(7):1797-1801.
[15]张文杰,邱清文,邱战洪.垃圾填埋场边坡稳定可靠度分析[J].岩石力学与工程学报,2010,29(增刊1):2958-2963.ZHANG Wen-jie,QIU Qing-wen,QIU Zhan-hong,Reliability analysis of stability of a municipal solid waste landfill[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(Supp.1):2958-2963.
[16]王伟,金鹏,张芳.短龄期城市固体垃圾直剪试验及应力位移模型[J].岩土力学,2011,32(增刊1):166-170.WANG Wei,JIN Peng,ZHANG Fang.Direct shear test of short-fill-age municipal solid wastes and its shear stress-deformation model[J].Rock and Soil Mechanics,2011,32(Supp.1):166-170.
[17]郭城,柯瀚.城市固体废弃物弹塑性蠕变降解模型探讨[C]//第一届全国岩土多场相互作用及环境土工学术研讨会.杭州:浙江大学出版社,2012.
[18]王磊,朱斌,李俊超,等.考虑纤维加筋作用的城市固废本构模型[C]//第一届全国岩土多场相互作用及环境土工学术研讨会.杭州:浙江大学出版社,2012.
[19]南京水利科学研究院.SL 237-1999 土工试验规程[S].北京:中国水利水电出版社,1999.
[20]张振营.城市生活垃圾的压缩性及填埋场的沉降研究[博士论文D].杭州:浙江大学,2005.
[21]张振营,严立俊.城市新鲜生活垃圾变形与强度的关联特性研究[J].浙江大学学报(工学版),待发表.ZHANG Zhen-ying,YAN Li-jun.Study on the relevant properties of the deformation and the shear strength of the fresh municipal solid waste[J].Journal of Zhejiang University(Engineering Science),in press.
