带投资组合和超额赔款的再保险双Cox风险模型

牛银菊，罗永丽，夏亚峰

(1.东莞理工学院计算机学院，广东东莞523808;2.兰州理工大学理学院，甘肃兰州730050)

0 引言

风险理论是当前精算数学界研究的热门课题.文献［1］介绍了带干扰的经典风险模型，文献［2-4］基于干扰条件对保费和索赔到达过程进行了推广.文献［5］利用效用理论讨论了确定停止损失再保险的数学模型，给出了最优自留额存在且唯一的充要条件.文献［6］利用线性规划证明了停止损失再保险的最优性，用鞅方法得到了破产概率的解析表达式及上界.关于 Cox 风险模型，J.Grandell［7］对此有深入地研究，得到了其破产概率的Lundberg不等式以及其他一些结论.文献［8-11］较为详细地研究了双险种且理赔次数服从Cox过程的风险模型，得到破产概率在特殊情况下的数学表达式.文献［12-14］建立了再保险的Cox风险模型，文献［15-16］建立了带干扰项的双Cox风险模型，得到了其破产概率明确的表达式及Lundberg不等式.在实际运营中，保险公司由于保险规模的不断扩大，保险的组织形式也需要建立多元化的模式，同时由于受通货膨胀、投资回报、自然灾害等因素的影响，保险公司有可能面临破产.为了规避破产的风险，保险公司通过签订分保合同，将其所承担的风险转给再保险公司.再保险是一种分散保险公司风险的有效方法，而破产概率又是度量风险的重要指标.为得到更符合保险公司实际情况的风险模型，本文建立带投资组合和超额赔款的再保险双Cox风险模型，得到了其Lundberg指数上界和破产概率的上界，并给出了最终破产概率的表达式.

1 模型的建立

给定概率空间(Ω，F，P).

定义1 随机过程{Λ(t)，t≥0}以概率1满足:

1)Λ(0)=0;

2)∀t＜+∞，Λ(t)＜+∞;

3)其样本轨道是关于时间t的连续函数且单调不减，以及当t→+∞ 时，Λ(t)→+∞，P-a.s.，则称Λ(t)为一个扩散的随机测度.

定义3 设Λ(t)是扩散的随机测度，{N(t)，t≥0}是累积强度为Λ(t)的Cox过程，{Zk，k≥1}是同分布的非负随机序列且相互独立，其均值为μ，分布函数为F(·)，且假定它们是相互独立的，再保险公司向分出保险的保险公司的第k次赔付额为

其中，m表示分出保险的保险公司自留赔付额的最大上限，zk表示所支付的第k次赔付额(k=1，2，3，…).

在引入本文的模型之前，还需要作如下假设:

(i)在时期［0，t］内收到的保费次数{N1(t)，t≥0}是强度为{Λ1(t)，t≥0}的Cox过程，每次收到的保费{Xk，k≥1}是独立同分布的随机变量，且与{N1(t)，t≥0}相互独立;

(ii)再保险公司所承担的险种在时期［0，t］内的理赔次数{N2(t)，t≥0}是强度为{Λ2(t)，t≥0}的Cox过程，每次的理赔额{Yk，k≥0}是相互独立的随机变量，且与{N2(t)，t≥0}相互独立;

(iii)再保险公司向分出保险的保险公司的理赔次数{N3(t)，t≥0}是强度为{Λ3(t)，t≥0}的Cox过程，每次的理赔额{zk，k≥0}相互独立的随机变量，且与{N3(t)，t≥0}相互独立;

(iv){N1(t)，t≥0}，{Xk，k≥1};{N2(t)，t≥0}，{Yk，k≥0};{N3(t)，t≥0}，{zk-h(zk)，k≥0}分别相互独立;

(v)假设投资组合收益率满足aW(t)+rt，其中a为干扰因子，W(t)为标准的布朗运动，r为漂移参数.

在上述假设下，考虑超额赔款再保险，建立带投资组合的再保险双Cox风险模型为

其中，u1表示保险公司的初始资金，u2表示用于投资的项目资金，r1表示u2的投资组合收益率(不包括投资管理成本和税收)，u3表示投资风险较大且收益不确定的项目资金，E［h(z)］表示再保险公司所承担赔付额的均值，ξ表示再保险公司受理再保险的相对安全系数，U(t)表示t时刻保险公司的盈余，u1＞ 0，u2＞ 0，u3＞ 0，r1＞ 0，r2＞ 0，a ＞ 0.

令 u=u1+u2+u3，b=r1u2+r2u3，

则U(t)=u+S(t).

令 ψ(u)=p(u+S(t)＜ 0，∃t≥0)，φ(u)=1- ψ(u)，Tu=inf{t≥0，u+S(t)＜ 0}，则称Tu为破产时刻，ψ(u)为保险公司的破产概率.

2 破产概率的上界

引理 1［7］如果 Λ(t)是随机测度，且假设E［Λ(t)］＜∞，= σ(Λ(t)，t≥0)，则N(t)是相应的Cox过程，当且仅当满足下列条件:

定理1 令Mu(t)=exp［-r(u+S(t))］［exp(-rS(t))］，则 Mu(t)是 Ft鞅.

证令FΛ1∞=σ(Λ1(t)，t≥0)，FΛ2∞=σ(Λ1(t)，t≥0)，FΛ2∞=，其中F(x)，G(x)，G1(x)分别是随机变量X，Y，Z的分布函数.

因此有

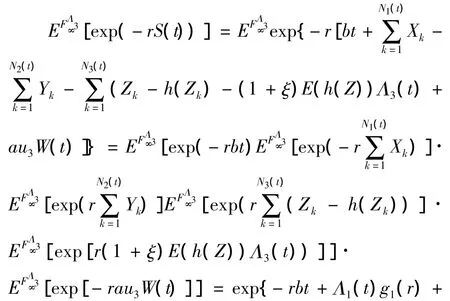
其中 g4(r)=g3(r)+r(1+ ξ)E(h(Z))，E(h(Z))=是再保险部分分布函数G1(x)的均值.

另一方面，有

因此，由(2)和(3)式有

所以Mu(t)是Ft鞅.

定理2 对于模型(1)，∀r＞0，破产概率ψ(u)≤e-ru·G(r)，其中

证设Tu是破产时刻，Tu是停时，设t0(＜∞)为常数，则易知t0∧Tu(≥0)是有界停时.由鞅的可选停时定理得

因此，

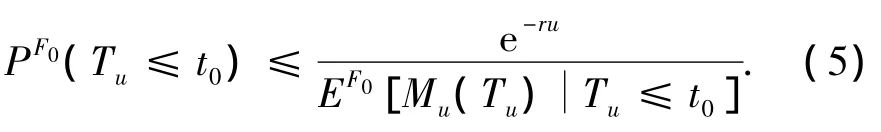
又由于Tu时刻保险公司破产，-r(u+S(Tu))≥0，故 exp［-r(u+S(Tu))］≥1，则

故(5)式可化为

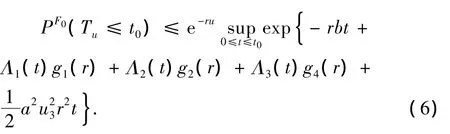
对(6)式两边取期望得

在上式两端令t0→+∞ 得

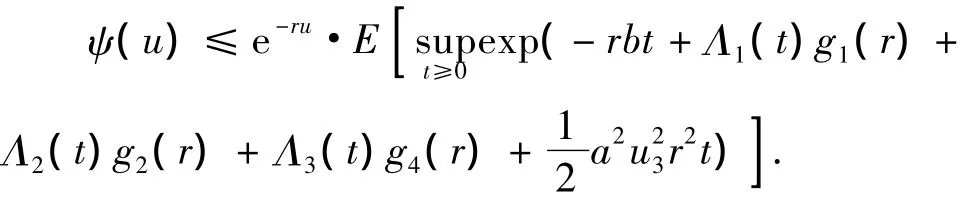
定理3 对于模型(1)，最终破产概率

证由于exp{-Ru}=M0(0)=E［Mu(t0∧t0］P［Tu≥ t0］，所以，当 t0→∞ 时，

又Tu＞t0，E［U(t0)］→∞(t0→∞)，由控制收敛定理得

(7)式变为

于是

以上结论表明，本文建立的风险模型与古典风险模型的结果相类似.

［1］ Dufresne F，Gerber HU.Risk theory for the compound Poisson process that is perturbed by diffusion ［J］.Insurance:Mathematics and Economics，1991，10(1):51-59.

［2］董英华，张汉君.带干扰的双Poisson风险模型的破产概率 ［J］.数学理论与应用，2003，23(1):98-101.

［3］于文广，黄玉娟.干扰条件下的一个破产模型的改进［J］.江南大学学报:自然科学版，2008，7(1):118-121.

［4］张相虎，边平勇.带干扰的多险种风险模型的破产概率［J］.经济数学，2007，24(2):130-133.

［5］刘琳.停止损失再保险最优自留额的确定及存在性讨论［J］.江西师范大学学报:自然科学版，2011，35(6):614-616.

［6］王丙参，魏艳华，戴宁.停止损失再保险与风险模型的有限时间破产概率［J］.江西师范大学学报:自然科学版，2013，37(2):206-209.

［7］Grandell J.Aspects of risk theory［M］.New York:Springer-Verlag，1991.

［8］曾霭林，林祥，张汉君.双险种的Cox风险模型［J］.数学理论与应用，2003，23(1):107-112.

［9］何树红，徐兴富.双Cox风险模型［J］.云南大学学报:自然科学版，2004，26(4):275-278.

［10］何莉娜，刘再明.一类Cox风险模型破产概率的研究［J］.广西民族学院学报:自然科学版，2006，12(2):80-82.

［11］杨圣举，李学萝，李文玲.双Cox风险模型中破产概率的上界［J］.南开大学学报:自然科学版，2009，42(1):34-43.

［12］洪圣光，赵秀青.再保险的Cox风险模型［J］.长春工程学院学报:自然科学版，2008，9(2):86-88.

［13］Nie Gaoqin.On the expected discounted penalty function of a kind of Cox risk process with variable premium rate and disturbed by diffusion［J］.Mathematical Theory andApplications，2009，29(3):11-15.

［14］Song Min，Wu Rong，Wang Guojing.On the joint distribution for a kind of Cox risk process［J］.Chinese Journal ofApplied Probability and Statistics，2010，26(6):597-604.

［15］解俊山，于吉亮，赵选民.带干扰双Cox风险模型的破产概率研究［J］.统计与决策，2007(6):27-28.

［16］张立飞，王勇.马氏环境下双 Cox风险模型的研究［J］.哈尔滨理工大学学报，2009，14(2):30-33.