关于图的Fractional控制数

徐保根，赵丽鑫，邹 妍

(华东交通大学理学院数学系，江西 南昌 330013)

0 引言及定义

本文所指的图均为无向简单图，文中未说明的符号和术语同于文献［1-2］.

设G为1个图，用V(G)和E(G)分别表示G的顶点集和边集.对于任意顶点v∈V(G)，定义v的邻域，闭邻域N［v］=N(v)∪为v点在G中的度，并且Δ=Δ(G)和δ=δ(G)分别表示图G的最大度和最小度.对于2个点不交的图G和H，则用G∨H表示G与H的联图，即在G∪H中将G的每个点与H的所有点邻接所成的图.

为了方便，若S⊆V(G)，f:V→R为1个实值函数，则记

下面给出关于图的Fractional控制的定义.

定义1［3］设G=(V，E)为1个图，实值函数f:V→［0，1］满足f(N［u］)≥1对一切u∈V(G)都成立，则称f为图G的1个Fractional控制函数(简称为F-控制函数).图G的Fractional控制数(简称为F-控制数)定义为

γf(G)=min{f(V)︱f为图G的F-控制函数}.且称满足γf(G)=f(V)的F-控制函数为1个最小F-控制函数.对于任何图G，由于常数函数f=1总是G的F-控制函数，故图G的F-控制函数和F-控制数均存在.

若H为图G的1个生成子图，则图H的任何F-控制函数也是图G的F-控制函数，因此有下面的引理1.

引理1 设H为图G的1个生成子图，则γf(G)≤γf(H).

由定义1不难看出，对任意n阶图G，均有1≤γf(G)≤n，并进一步可得引理2 对任意n阶图G，均有1≤γf(G)≤n，并且有

(i)γf(G)=n当且仅当为空图;

(ii)γf(G)=1当且仅当Δ(G)=n-1.

定义2［4］设G=(V，E)为1个图，实值函数f:V→［0，1］满足f(N［u］)≤1对一切u∈V(G)都成立，则称f为图G的1个F-包装函数.图G的(上)F-包装数定义为Pf(G)=max{f(V)︱f为图G的(上)F-包装函数}，并且称满足Pf(G)=f(V)的(上)F-包装函数为1个最大F-包装函数.

引理3 对任意图G，均有Pf(G)=γf(G).

由文献［3］和引理3可导出F-控制数的界限.

引理4 对任意n阶图G，均有

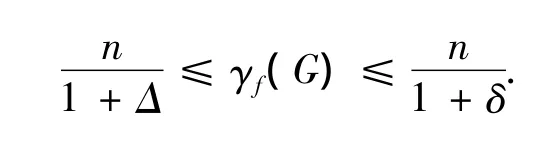
特殊地，当G为n阶r-正则图时，则

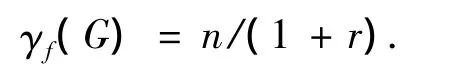
由上述2个定义及引理3可知，对于1个给定图G，如果存在实值函数 f:V→［0，1］，使得 ∀u∈V(G)均有f(N［u］)=1成立，则函数f既是G的最小F-控制函数，又是G的最大F-包装函数，从而有下面的结论成立.

引理5 设G为1个图，如果存在实值函数f:V→［0，1］，使得 ∀u∈V(G)均有f(N［u］)=1成立，则 γf(G)=Pf(G)=f(V(G)).

利用引理4可确定一些特殊图的F-控制数，如完全二部图Km，n等.

引理6 设2≤s≤r且它们均为整数，则

1988年，G.S.Domke等［3］首次提出且研究了图的F-控制问题，E.O.Hare等［5-6］分别研究了关于乘积图的F-控制数，文献［7］讨论了乘积图的边控制问题.本文先确定完全t-部图的F-控制数(t≥2)，从而推广了引理6的结果，并给出关于联图的F-控制数的1个上界，由此导出一些特殊联图的F-控制数.

1 主要结果及证明

首先给出完全 t-部图 K(n1，n2，…，nt)的 F-控制数(t≥2).

定理1 设n1≥n2≥…≥nt≥2且它们均为整数(t≥2)，，则

证 记 G=K(n1，n2，…，nt)，V(G)=V1∪V2∪…∪Vt为其t-部顶点划分［8］，其中(1≤i≤t).定义图G上的1个实值函数f:V(G)→［0，1］如下:

对于每个Vi(1≤i≤t)，当u∈Vi时，令f(u)=1/［(T+t-1)(ni-1)］.

因t≥2且n1≥n2≥…≥nt≥2，故0≤f(u)≤1，并且有

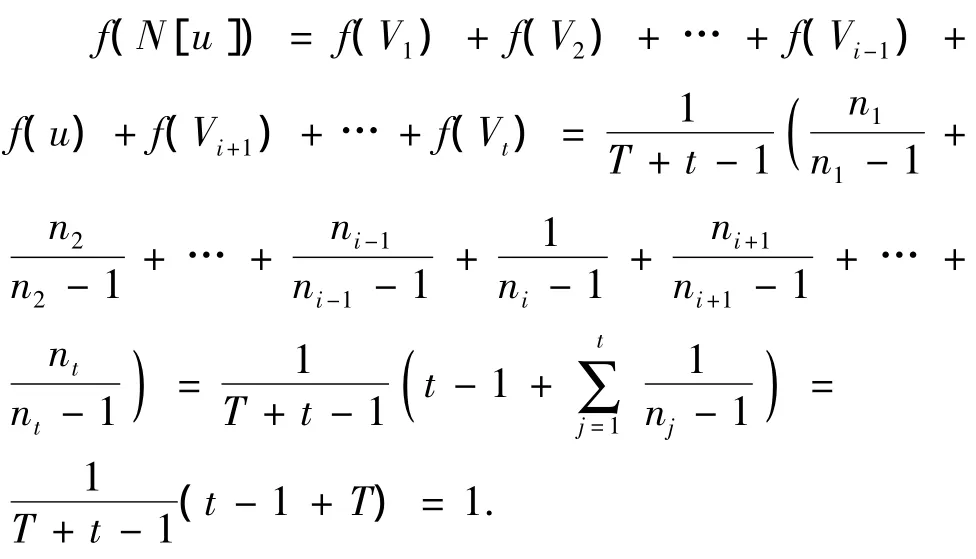
由u点的任意性知，∀u∈V(G)，均有f(N［u］)=1成立.由引理5得

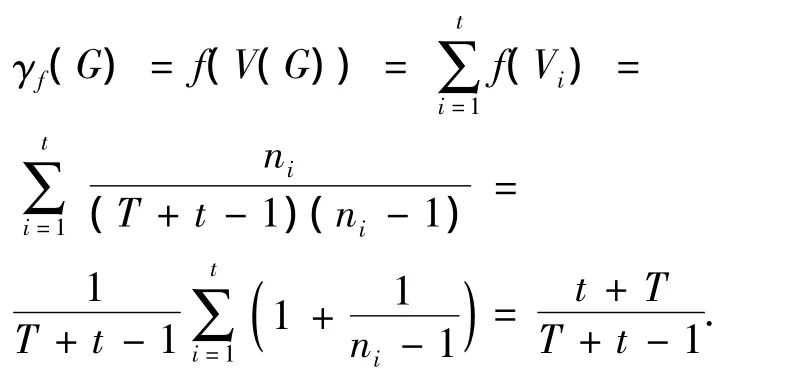
定理1得证.

特殊地，当 t=2，n1=r，n2=s时，T=1/(r-1)+1/(s-1)，代入定理1中即得到引理6的结论.

下面考虑关于联图的F-控制数［9-11］.

定理2 设G和H为2个点不交的图，则

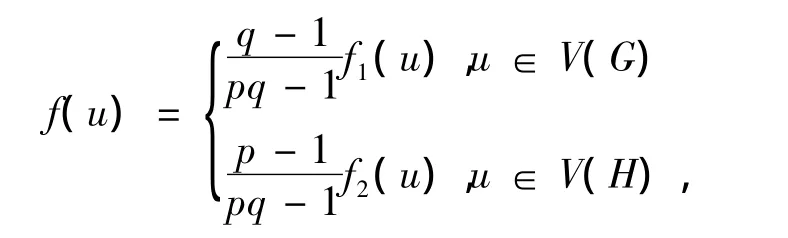
由于f1和f2分别为图G和图H的F-控制函数，故有0≤f1(u)≤1，0≤f2(u)≤1.注意到p=γf(G)＞1，q=f2(V(H))＞ 1，可知0≤f(u)≤1.

∀u∈ V(G∨ H)，不妨设 u∈ V(G)，由于f1(NG［u］)≥ 1，故有

因此，实值函数f为联图G∨H的1个F-控制函数，从而有

即(pq-1)γf(G∨H)≤(q-1)p+(p-1)q.定理2得证.

在定理2的证明中不难看出，如果分别存在图G和图H的F-控制函数f1和f2，使得f1(N［u］)=1对任何u∈V(G)成立，并且f2(N［v］)=1对任何v∈V(H)成立，则定理2中等式成立.

推论1 设G和H为2个点不交的图，如果分别存在图 G和图 H的 F-控制函数 f1和 f2，使得f1(N［u］)=1且f2(N［v］)=1对任何u∈V(G)和v∈V(H)成立，则有

由推论1可以确定一些特殊联图的F-控制数.

引理7 设整数n≥3，Pn和Cn分别表示n阶路和n阶圈，则

(i)γf(Cn)=n/3，且存在 Cn的F-控制函数 f，使得f(N［u］)=1对任何u∈V(Cn)成立;

(ii)γf(Pn)=「n/3⏋，且存在Pn的F-控制函数f，使得f(N［u］)=1对任何u∈V(Pn)成立.

证 (i)由引理4知γf(Cn)=n/3，并取Cn上1个常数函数f=1/3，显然有f(N［u］)=1对任意u∈V(Cn)成立.

(ii)记 V(Pn)={v1，v2，…，vn}，且 E(Pn)=.下面分2种情形定义Pn上的函数f如下:

不难验证，f(N［u］)=1对任何u∈V(Pn)成立.由引理5得

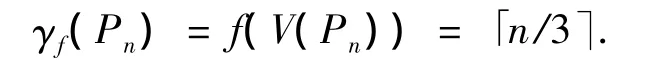
引理7得证.

由引理7及推论1可直接得出下面的结论.

定理3 设m≥4和n≥4，且它们均为整数，记

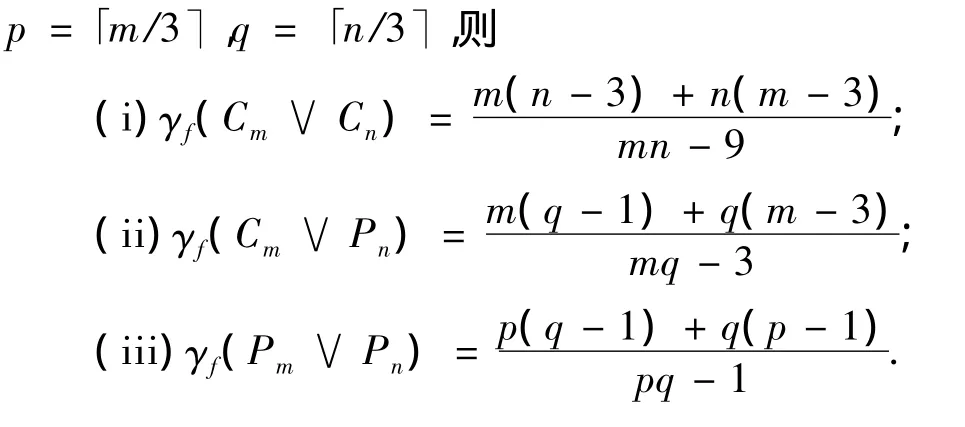
［1］ Bondy JA，Murty V SR.Graph theory with applications［M］.Amsterdam:Elsevier，1976.

［2］Haynes TW，Hedetniemi S T，Slater P J.Domination in graphs［M］.New York:Marcel Dekker，1998.

［3］Domke G S，Hedetniemi ST，Laskar R C.Fractional packings，coverings and irredundance in graphs［J］.Congr Numer，1988，66:227-238.

［4］徐保根.图的控制与染色理论［M］.武汉:华中科技大学出版社，2013.

［5］Hare E O.K-weight domination and fractional domination of Pm× Pn［J］.Congr Numer，1990，78:71-80.

［6］ Fisher D C.Domination，fractional domination，2-packing and graph products ［J］.SIAM Discrete Math，1994，7(3):493-498.

［7］徐保根，陈悦.图的符号边全K控制数［J］.江西师范大学学报:自然科学版，2011，35(3):316-318.

［8］徐保根，赵利芬，操叶龙，等.关于图的控制集划分［J］.江西师范大学学报:自然科学版，2013，37(5):475-478.

［9］齐登记，梁希泉.关于图的控制数Vizing's定理的推广［J］.东北师大学报:自然科学版，2005，37(1):24-27.

［10］周仲旺，刘书英.一类联图的符号边控制数［J］.数学的实践与认识，2013，43(16):255-261.

［11］徐保根，张亚琼，汤友良.关于图的符号边控制数的一些结论［J］.河南科技大学学报:自然科学版，2012，33(4):74-77.