基于模拟退火的万有引力算法

王立平，肖乐意

(1.萍乡学院，江西 萍乡337000;2.长沙师范学院教务处，湖南 长沙410100)

0 引言

在科学、经济和工程领域中，许多最新的进展都依赖于全局优化技术，即计算出相应优化问题的全局最优解的数值技术［1］.在全局优化技术中，启发式搜索算法是目前比较流行且行之有效的一类优化技术.目前比较流行的启发式搜索算法有粒子群优化算法［2］、模拟退火算法［3］、类电磁机制算［4］、遗传算法［5］、蚁群算法［6］、万有引力算法［7］等.尽管该类算法为求解复杂优化问题提供了较多有效的途径，但其结果仍不能令人满意，如算法易陷入局部最优、解的精度不高等.而且多数启发式算法没有形成系统的理论，没有统一的算法框架，有许多问题仍有待研究［8］.

万有引力算法(A gravitational search algorithm，GSA)是伊朗的克曼大学教授Esmat Rashedi等于2009提出来的，该算法基于牛顿万有引力定律，通过模拟粒子间相互作用的万有引力指导粒子进行搜索，由文献［7］可知万有引力算法与中心力算法、粒子群算法相比，具有明显的优越性.然后，由于移动步骤具有一定盲目性，可能造成个体退化;且万有引力算法无局部搜索机制，因而局部搜索能力较弱.

针对GSA的上述缺陷，本文提出了一种基于模拟退火的万有引力算法(gravity algorithm based simulated annealing，GABSA)，该算法采用模拟退火算法的Metropolis准则对移动步骤进行判断，从而减少移动的盲目性;同时通过采用模拟退火算法进行局部搜索，提高局部搜索能力.实验结果表明:GABSA的优化效果明显优于GSA.

1 模拟退火算法

模拟退火算法(simulated annealing，SA)的思想最早是由 Metropolis于1953年提出来的，1983年Kirkpatrick将其应用于组合优化问题，SA算法基于固体物质的退火过程，是一种通用的优化算法，已成功应用于解决车辆路线优化、TSP问题、车间调度问题等优化问题［9－11］.

模拟退火算法基本思想是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性.模拟退火算法从某一较高初温出发，伴随温度参数的不断下降，结合概率突跳特性在解空间中随机寻找目标函数的全局最优解，即在局部最优解能概率性地跳出并最终趋于全局最优.

Metroplis准则:设粒子初始状态为i，随机摄动得到粒子的一个新状态j.E(i)、E(j)分别为粒子在状态 i、j时的能量:

(i)若E(j)＜E(i)，则状态转换被接受;

(ii)若E(j)≥E(í)，则状态转换的概率为

Pij=exp(－(E(j)－E(i))(KT))，其中K为物理学中的玻耳兹曼常数，T为材料的温度.对同样的接受概率.模拟退火算法的基本步骤见文献［12］.

2 万有引力算法

万有引力算法基于牛顿万有引力定律:“任意2个质点通过连心线方向上的力相互吸引.该引力的大小与它们的质量乘积成正比，与它们距离的平方成反比，与2物体的化学本质或物理状态以及中介物质无关”.用公式表示为

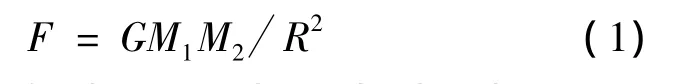
其中F为代表万有引力的大小，G为引力常数，M1、M2为代表2个粒子的惯性质量，R为2个粒子之间的欧氏距离.

粒子j对粒子i的吸引力在d维上的分量为［7］

因为实验表明R比R2效果更好，所以采用R代替R2;Maj表示施力粒子j的质量，Mpi表示受力粒子i的质量;ε为一小常量，G(t)为时间 t下的引力常量:

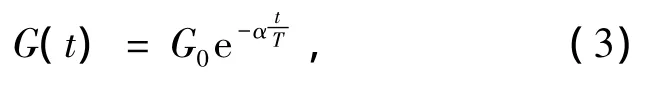
其中G0为引力常量初始值，α为一常量，T为算法的总迭代次数.

粒子i在d上的合力为

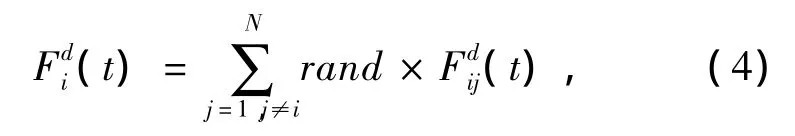
其中rand是为增加算法搜索的随机性而增加的随机量，其取值范围为［0，1］.

由牛顿第二定律可知:在时间t时，粒子i在d上的加速度为

其中Mi(t)为粒子i的惯性质量.在GSA算法中，使用以下公式更新粒子的惯性质量为

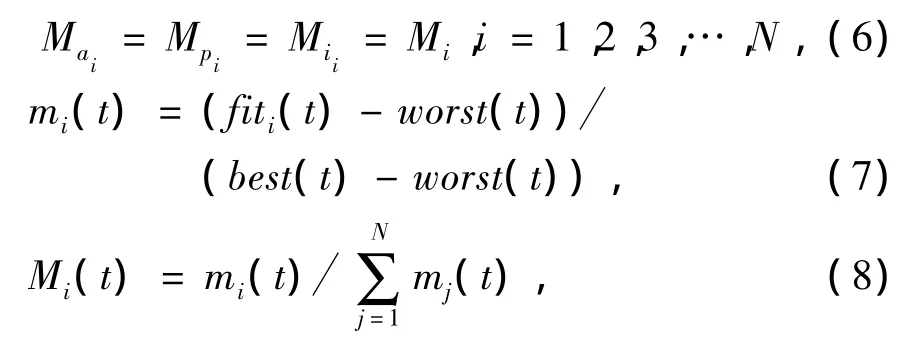
其中fiti(t)为t时粒子i的适应值，对于求最小值问题时，worst(t)、best(t)为

在GSA算法中，每次迭代都会按照牛顿运动定律对粒子的运动状态进行更新，更新公式为

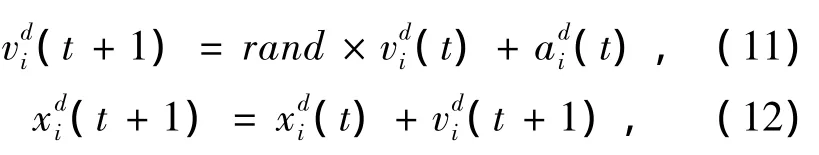
3 基于退火思想的算法改进

3.1 基于Metropolis准则的位置更新策略

由(12)式可见，粒子的位置更新具有一定的随机性，从而使个体可能会从适应值高的位置移到适应值低的位置，这种现象称为个体的退化;即可能造成fiti+1(t)＞fiti(t)(求最小值问题时)，这对问题的求解显然是不利的.针对万有引力算法的这一不足，本文提出一种基于Metropolis准则的粒子位置更新策略:(i)根据式(12)计算出粒子i下一个可能的位置i(t+1);(ii)根据Metropolis准则判断是否接受i(t+1)作为i的下一个位置.具体如下:若fiti+1(t)≤fiti(t)或 rand≤exp(－fiti+1(t)－fiti(t)(KT))，则xi(t+1)=(t+1);否则xi(t+1)=xi(t).其中fiti+1(t)为假设i的下一位置为i(t+1)时的适应值，rand为［0，1］上的随机数.

可见，当粒子从一个适应值优的位置移到一个适应值更差的位置时，通过Metropolis准则的引导，只以一定概率接受差解，一定程度上避免了粒子的退化.

3.2 基于模拟退火的万有引力算法

由文献［7］可知，万有引力算法全局搜索能力较强;但是从算法具体步骤可见，引力算法缺乏局部搜索机制，因此算法的局部搜索能力比较弱.而退火算法虽然前期的全局能力不强，却具有快速搜索到局部最优解的能力［13］.因此，本文将万有引力算法与退火算法融合，使算法同时兼顾全局和局部搜索能力.

基于模拟退火的万有引力算法以万有引力算法框架为基础［7］，采用基于Metropolis准则的粒子位置更新策略;同时在万有引力算法操作完成后，采用退火算法对最优个体进行操作，增加算法的局部寻优能力.算法的具体步骤如下:(i)初始化操作.包括初始种群Q、引力常量初值G0、退火初始温度T0、玻耳兹曼常数K、迭代次数N等;(ii)计算粒子适应值;(iii)更新引力系数G(t)、最好值best(t)、最坏值worst(t)和粒子的惯性质量Mi(t);(iv)按(4)式计算各粒子各方向上的力的总和;(v)分别按(5)式和(11)式计算各粒子的加速度和速度;(vi)(12)式计算各粒子下一步可能的位置，用基于Metropolis准则的粒子位置更新策略对粒子的位置进行更新;(vii)判断是否迭代结束，如未结束，则返回步骤3)重复执行;(viii)对最优个体进行退火操作;(ix)输出结果.流程图如图1所示.

4 算法性能测试

4.1 性能测试一

为了测试退火思想引入的有效性，将本文算法与文献［7］万有引力算法进行比较，表1为测试函数［14］，函数 F1、F2的最大迭代次数为 50，F3的最大迭代次数为100，优化精度为0.1，算法其它参数见表2，表3为本算法与文献［7］GSA的性能比较.图2～图4分别为函数F1～F3优化效果比较图.

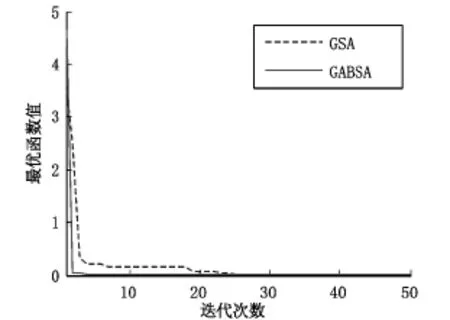
图2 F1寻优曲线

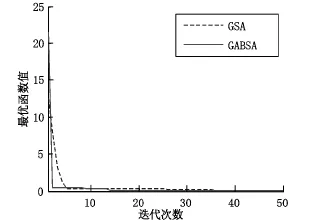
图3 F2寻优曲线

表1 测试函数一

表2 算法参数

表3 GABSA与GSA性能比较

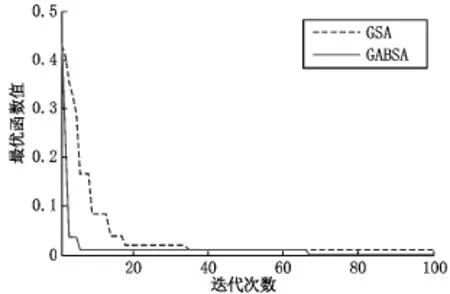
图4 F3寻优曲线

由表1可见，GABSA在成功率、求解精度上比GSA好;图2～图4表明GABSA的收敛速度比GSA快，收敛精度比GSA高.退火思想的引入，使得GABSA具有更快的收敛速度、更高的成功率和求解精度.这是由于:(i)Metropolis准则的个体移动策略，一定程度避免了个体移向更差解;(ii)对最优个体进行退火搜索，提高了算法收敛速度与搜索精度.

4.2 性能测试二

为了进一步对算法的性能进行测试，将本文算法与文献［15］的一种群体迁移优化算法(speciesmigrationbased optimization algorithm，SMOA)进行比较.为了更好地测试算法性能，选取文献［15］的高维函数作为测试函数，实验结果见表5，其中SMOA测试数据来自文献［15］.实验参数:种群规模为30，进化代数为50，独立运行50次.

表4 测试函数二

表5 GABSA与SMOA性能比较

由表5可见，对于高维函数的求解，GABSA比SMOA有更高的求解精度.故GABSA具有较好的收敛效果与求解精度，具有优越的寻优性能.

5 结束语

本文针对GSA算法存在的不足，通过采用基于Metropolis准则的个体移动策略，并对最优个体进行退火操作，提出了一种基于模拟退火思想的万有引力算法(GABSA).通过测试实验，将GABSA与GSA进行比较，验证退火思想引入的有效性;GABSA与文献［15］的SMOA求解高维函数进行的比较，进一步验证了GABSA的有效性.

［1］王晓娟，高亮，陈亚洲.类电磁机制算法及其应用［J］.计算机应用研究，2006，23(6):67－70.

［2］ Karakuzu J，Eberhart R C.Particle swarm optimization［J］.IEEEInternational Conference on Neural Networks，1995，4:1942－1948.

［3］Suman B，Kumar P.A survey of simulated annealing as tool for single andmuhiobjective optimization［J］.Journal of the Operational Research Society，2006，57(10):1143－1160.

［4］Birbil SI，Fang S C.An electromagnetism－likemechanism for global optimization ［J］.Journal of Global Optimozation，2003，25(3):263－282.

［5］Tang K S，Man K F，Kwong S，et al.Genetic algorithms and their applications［J］.IEEE Signal Processing Magazine 1996，13(6):22－37.

［6］Dorigo M，Birattari M，Stutzle T.Ant colony optimization artificial ants as a computational intelligence technique［J］.IEEE ComputationalIntelligence Magazine，2006，1(4):28－39.

［7］Esmat Rashedi，Hossein Nezamabadipour，Saeid Saryazdi.GSA:a gravitational search algorithm ［J］.Information Sciences，2009，179(13):2232－2248.

［8］谢丽萍，曾建湖.受拟态物理学启发的全局优化算法［J］.系统工程理论与实践，2010，30(12):2276－2282.

［9］Suman B，Kumar P.A survey of simulated annealing as a tool for single andmultiobjective optimization［J］.Journal of the Operational Research Society，2006，57(10):1143－1160.

［10］ElBouriA，Azizi N，Zolfaghari S.A comparative study of a new heuristic based on adaptivememory programming and simulated annealing:the case of job shop scheduling［J］.European Journal of Operational Research，2007，177:1894－1910.

［11］Tan K C，Chew Y H，Lee L H.A hybridmulti－ob jective evolutionary algorithm for solving truck and trailer vehicle routing problems［J］.European Journal of Operational Research，2006，172:855－885.

［12］杨勇，谭渊，张晓发，等.基于模拟退火算法的阵列模型有源校正方法［J］.国防科技大学学报，2011，33(1):91－94.

［13］王银年，葛洪伟.求解TSP问题的改进模拟退火遗传算法 ［J］.计算机工程与应用，2010，46(5):44－85.

［14］吴涛，金义富.基于云控制的自适应遗传算法［J］.计算机工程，2011，37(8):189－191.

［15］马海平，李寰，阮谢永.一种群体迁移优化算法及性能分析［J］.控制理论与应用，2010，27(3):329－33.