关于高等数学中分段函数的讨论
2014-01-16费彦宏
费彦宏,李 茜
(山西运城农业职业技术学院,山西 运城 044000)
1 分段函数的定义
有时一个函数要用几个式子表示,这种在自变量的不同变化范围中,对应法则用不同式子来表示的函数,通常称为分段函数.
若分段函数在点x0两侧的表达式不同,则将点x0称为分段点,也可称为分界点.
例如,函数
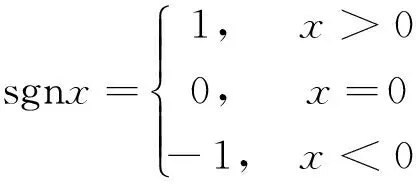
函数
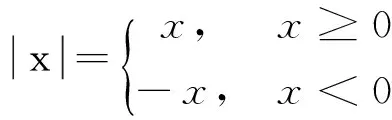
注意:分段函数是一个函数,而不是几个函数.
2 分段函数在点x0处的函数值
结论:要求分段函数在点x0处的函数值,应先确定点x0所在的自变量的取值范围,再按相应的表达式进行计算.
例1 设函数
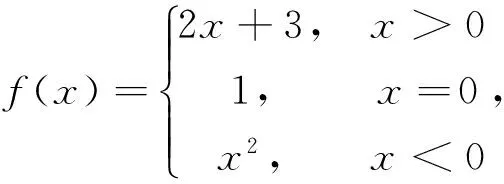
解:显然,f(0)=1
∵-1<0,∴f(-1)=(-1)2=1
∵1>0,∴f(1)=2×1+3=5
3 分段函数在点x0处的极限
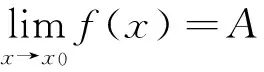
结论:要求分段函数在点x0处的极限,应首先判断x0是否为分段点
(Ⅰ)若x0是分段点,则应先求出x0处的左、右极限,再根据极限存在的充 要条件,从而得出在x0处的极限
(Ⅱ)若x0不是分段点,有两种情况[1]94-95:
a.先确定x0所在的自变量的取值范围,再利用相应的表达式求出在x0处的极限
b.直接利用极限的定义求
例2 函数
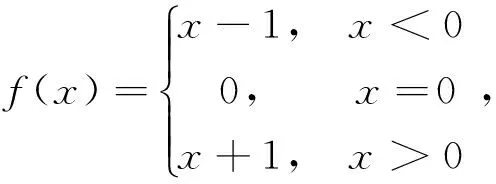
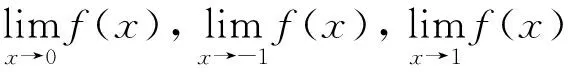
解:(Ⅰ)显然,x0=0是分段点
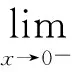
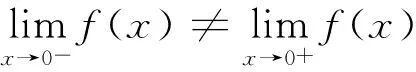
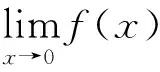
(Ⅱ)显然,x0=-1不是分段点
(Ⅲ)显然,x0=1不是分段点
例3 设函数
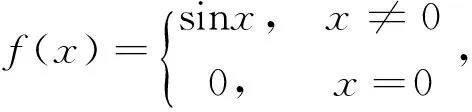
解:显然,x0=0不是分段点
4 分段函数在点x0处的连续性与可导性
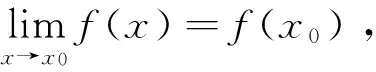
由上述定义可得以下结论[2]35-37
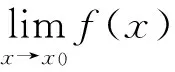
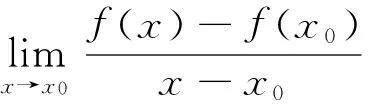
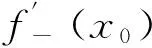
可导与连续的关系:若函数y=f(x)在点x0处可导,则在该点必连续.
另一方面,一个函数在某点连续却不一定在该点处可导.
由可导与连续的关系,可得下面结论,
结论:要讨论函数f(x)在点x0处的可导性与连续性,可先判断在x0处的连续性,再判断可导性. 具体如下:
(Ⅰ) 若在x0处不连续,则在x0处不可导.
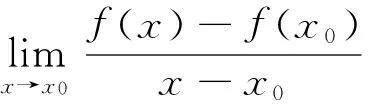
例4 讨论例2中函数f(x)在x=0处的可导性与连续性
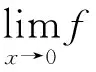
例5 讨论例3中函数f(x)在x=0处的可导性与连续性
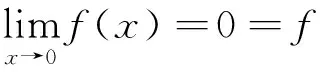
∴f(x)在x=0处可导.
例6 讨论函数
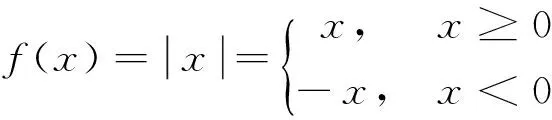
解:显然,f(x)在x=0处连续,而x=0是分段点,
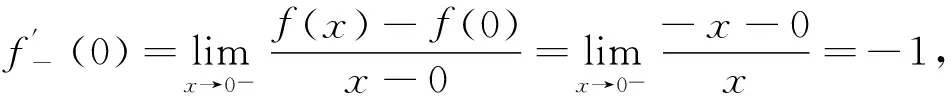
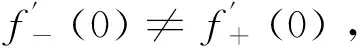
5 分段函数的不定积分
结论:要求分段函数的不定积分,应先分别求出自变量的各取值范围上的不定积分,再根据连续性确定各积分常数.
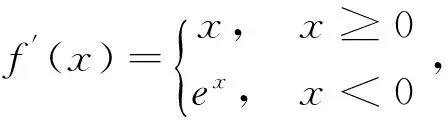
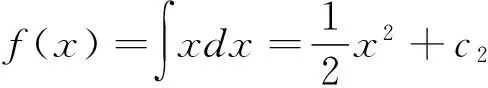
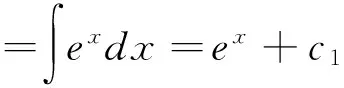
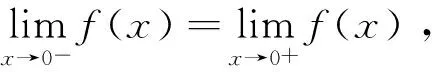
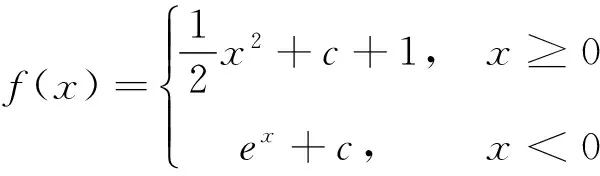
6 分段函数的定积分
结论:要求分段函数的定积分,应先进行分段积分,然后相加.
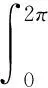
解:
=1-(-1-1)-(-1)
=4
[1] 王晓东. 分段函数在教学过程中的问题探析[J]. 漯河职业技术学院学报,2008,7(2).
[2] 何 波,岳卫芬. 试论分段函数的特征[J]. 高等函授学报(自然科学版),2004,17(6).
