城轨列车反推自动停车控制算法
2014-01-16张梦楠徐洪泽
张梦楠,徐洪泽
(北京交通大学轨道交通控制与安全国家重点实验室,100044,北京)
城轨列车自动驾驶系统(ATO)主要用于列车 运行速度和运行状态的自动控制,是列车安全、高效运行的重要保障。自动停车是ATO系统的重要功能之一,即实现列车在站台或屏蔽门处的精确制动。对于城轨列车,停车点处误差需要控制在±(0.3~0.5)m之间。因此,设计高性能的自动停车控制器以满足停车精度的苛刻要求是十分必要的。
列车停车精度主要受到2个因素的制约。首先,闸瓦摩擦系数的非线性是导致停车精度下降的一个重要原因[1]。由于闸瓦摩擦系数受到闸瓦材料、列车运行速度的影响,因此其实际值与理论设计值会存在一定偏差,从而使制动力偏离设计值。制动系统的动态特性是影响停车精度的另一个因素[2]。实际的制动力在制动指令发出后通常要经过一定时间才能达到期望值,如果这一过渡过程在控制器设计阶段被忽略,那么实际的停车点将严重偏离期望的停车点。
早期的列车控制系统采取PID控制方法,根据运行模式控制列车的目标速度[2]。现阶段,针对列车控制系统的非线性特性,控制器通常采用智能化方法,如模糊控制、预测控制和神经网络控制[3-4]。文献[5]从能耗的观点提出用遗传算法对列车运行过程进行优化。为处理列车模型中的不确定参数,控制器同时采取了自适应控制策略[6-7]。文献[7]基于Pade近似和自适应方法处理制动模型中的时滞及外部扰动。尽管上述方法从不同方面提升了控制器的性能,但被控对象中的非线性和输入时滞这2个问题仍然没有得到充分的解决。
近年来,研究人员针对时滞系统相继提出了很多与延时相关的研究成果,常用的反推技术也被扩展到时滞系统的控制中[8]。但是,由于控制器无法利用当前时刻状态,所以输入时滞系统的控制仍然是一个开放的问题[9]。Bekiaris等利用反推技术处理了具有输入延时、状态延时的线性系统[10],Mazenc等则进一步将反推控制策略扩展到具有时滞的非线性系统中[11-12]。然而,上述方法由于对实际应用中的输入时滞、非线性等问题缺少分析,因而使用受到限制。
本文提出一种新型反推自动停车控制器,用以消除制动过程中闸瓦摩擦系数的非线性特性以及系统输入时滞的影响,实现城轨列车的自动停车控制。首先,建立了描述列车制动动态特性的非线性数学模型,克服了传统模型中制动减速度难以测量的缺点;接着,基于Krasovskii泛函算子研究了当前时刻状态与过去时刻状态之间的关系,并结合反推技术设计了自动停车控制器,使制动系统镇定;最后,利用Matlab仿真软件对制动系统进行了数值仿真,结果表明,该方法在获得理想的停车精度的同时保证了列车运行的平稳性。
1 电空制动系统模型
1.1 电空制动系统工作原理
电空制动系统已广泛应用于高铁、城市轨道交通中,其信号流和单轮物理模型如图1所示。图中的信号流包括微制动控制单元(MBCU)、电空阀、中继阀以及基础制动装置。首先,MBCU根据控制器发出的制动减速度指令β0产生对应制动力的电信号I0,电空阀将I0转化为空气压力信号p0,中继阀实现流量放大功能,使制动缸内的压力p迅速达到p0。基础制动装置包括制动缸和制动闸瓦,是产生最终制动力的实际装置。闸瓦作用在车轮上的压力为K,车轮与闸瓦之间的摩擦系数为μ。根据力矩平衡原理,实际制动力B=Kμ。
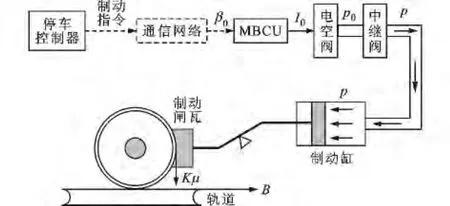
图1 电空制动系统示意图
1.2 电空制动系统数学模型
理想制动力计算公式为

式中:B0为理想制动力;kb为比例系数;μ′为理想闸瓦摩擦系数;p0为制动缸内的标准压强[13]。同样,列车的实际制动力计算公式为

式中:B为实际制动力;μ为实际闸瓦摩擦系数;p为制动缸内的实际压强。
制动缸压强的动态特性描述为

式中:T为制动缸的时间常数[13-14]。
取列车运行方向为正方向,由式(2)和式(3)得
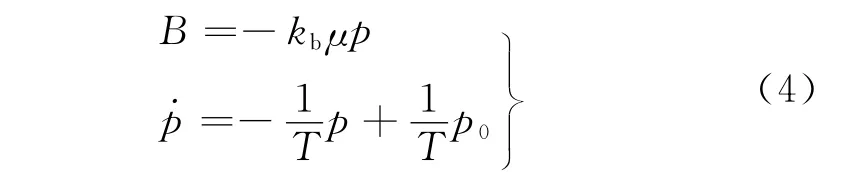

式中:β=B/mb为实际制动减速度;β0=B0/mb为控制器输出,表示期望制动减速度。
实际上,闸瓦摩擦系数为列车速度v的非线性函数,μ=μ(v),其表达式为
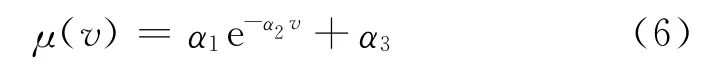
式中:α1、α2和α3为未知正常数,其值可由实验得到。由文献[14],闸瓦摩擦系数的表达式为
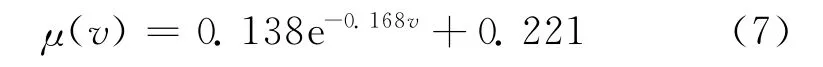
实际制动控制中闸瓦摩擦系数的设计值通常取为μ′=α3=0.221。
除了非线性特性,列车制动系统中还同时存在时滞现象。引起输入时滞的因素很多,包括压力空气的传播速度,MBCU计算和分配制动减速度的时间,电空阀、中继阀的响应时间等。用参数τ表示制动系统中全部的时滞。
基于上述分析,制动系统非线性数学模型为

式中:x1为列车的位置;x2为列车的速度;u(t)为停车控制器发出的制动指令,其物理意义为期望的减速度;τ为制动系统延时;g(x2)=0.624e-0.168x2+1;¯z=kbμ′p/mb。由于列车装备了速度传感器、位置传感器、压力传感器以及空气弹簧,因此状态变量均为可测的。控制系统框图如图2所示,图中的s为拉普拉斯算子。
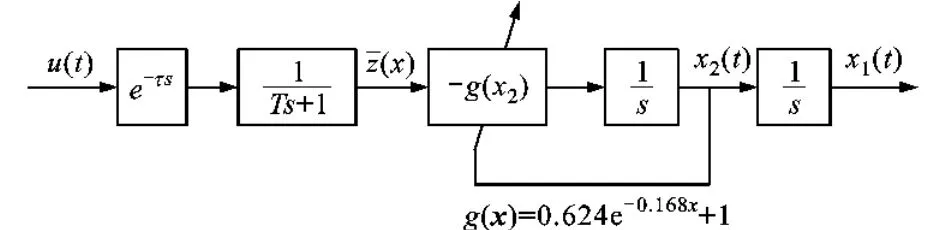
图2 控制系统框图
2 自动停车控制器设计
2.1 自动停车控制器设计目标
列车的制动过程可以由速度-位置曲线来描述。假设列车的初始位置-xr<0,状态变量x1∈[-xr,0];列车初始速度v0>0,状态变量x2满足x2∈[0,v0];期望的停车点为原点。那么,城轨列车实际制动的速度-位置曲线如图3所示。

图3 城轨列车制动曲线
控制器的设计目标为:列车制动初始位置为-xr,制动初始速度为v0,在保障列车运行平稳性的前提下,基于制动系统(8)设计自动停车控制器u(t),使得列车准确地在坐标原点处停车。
2.2 自动停车控制器设计
令¯z(t)=z(t)/T,式(8)可以重写为

显然,z(t)为无延时子系统的虚拟输入。由于无延时子系统具有下三角结构,因此可以通过经典的反推控制策略设计z(t),使子系统渐近稳定。
步骤1 令z1=x1,为使无延时子系统第一个方程渐进稳定,x2的期望值
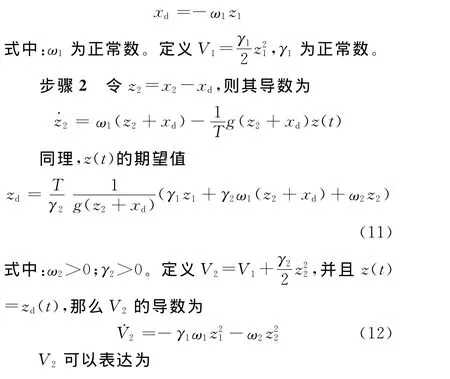
为一正定函数[15]。
步骤3 基于反推控制思想,实际控制器u(t)=u(x,~z)应当使得状态变量~z→0,t→∞。将~z(t)用2个Krasovskii泛函算子来表达,即Ψ:Cin→R和Π:Cin→R,有

式中:Cin=C([-τ,0],Rp)表示定义域为[-τ,0]、值域在集合Rp上的全部连续函数,p为正整数;xt(·)表示xt(θ)=x(t+θ),-τ≤θ≤0;φ(θ)表示函数x(·)的初始状态,即x(t0+θ)=φ(θ),-τ≤θ≤0,t0为初始时刻;L为负常数。
引理1 针对系统(15),设计控制器

则Krasovskii泛函算子Π(t)以指数收敛到0。证明 由Π(t)的定义可得
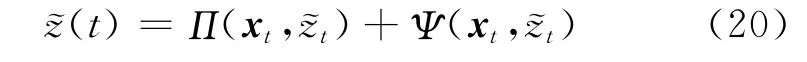
将控制器(19)代入到Π(t)的导数中,可得
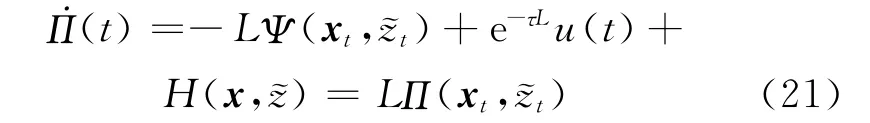
由于L<0,故Π(t)以指数收敛于0。证毕。
下面提出系统的可镇定条件假设、延时假设以及边界条件假设。
假设1 对于∀x1∈[-xr,0]和x2∈[0,v0],存在常数c1、c2和c3,满足

式中:G1(x)为非负函数。
假设2 系统延时τ及常数c1~c3满足如下不等式

假设3 列车制动初始位置为-xr,初始速度为v0,|βmax|为最大制动减速度,则上述变量满足:/2|βmax|;系统状态变量满足x1∈[-xr,0],x2∈[0,v0],z∈[0,|δβmax|],其中δ为比例系数;状态变量均为连续的且一阶导数存在。
基于上述分析,当制动系统满足假设1~3,则闭环自动停车控制器(19)可以表示为

2.3 自动停车控制器性能分析
首先引入Krasovskii泛函算子γ:Cin→R

选取参数c5~c9及kΠ如下

根据c2的定义,式(32)可进一步化为
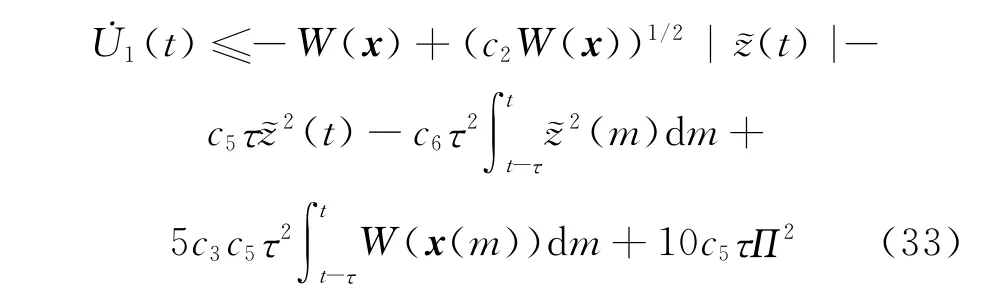
根据式(30)和(33),U2的导数满足


由于c1~c9均为正常数,所以Krasovskii泛函的导数为负定的。根据文献[15-16],泛函U(t)满足Lyapunov-Krasovskii稳定性定理对初始条件的要求,因此可得制动系统(8)、(9)为一致渐近稳定的[16],即列车在期望的停车点处准确停车。
3 数值仿真
为验证自动停车算法的有效性,在Matlab/Simulink环境下对非线性时滞系统进行了数值仿真。仿真基于地铁动车组实际制动过程,列车最大制动减速度为-1.2m/s2,为保证列车的平稳性,实际的制动减速度不超过最大制动减速度的限制;列车初始制动速度为72km/h,初始制动位置为-290m;制动缸压力的上升时间常数为1.5s,即T=0.65s;制动系统输入延时τ=0.4s,制动时间约为75s。Matlab/Simulink仿真框图如图4所示。
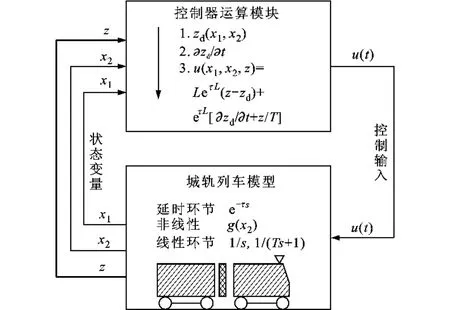
图4 仿真结构框图

图5 列车的位置曲线和速度曲线
列车制动过程的位置曲线和速度曲线如图5所示,列车实际停车曲线如图6所示。图5和图6显示,自动停车反推控制器克服了制动模型中非线性、输入时滞等因素的影响,实现了城轨列车的自动停车功能,表明控制器对输入时滞具有良好的鲁棒性。列车的速度曲线和位置曲线均以过阻尼的形式收敛到原点,避免了振荡,体现了列车的平稳制动过程。实际停车曲线显示列车准确地在期望停车点处停车,获得了较高的停车精度。由图6可见,在制动的初始阶段,由于系统输入延时的存在,列车会保持初始制动初速度不变继续运行一段距离,而高性能的停车控制器合理地补偿了这一距离对停车精度造成的影响。
列车实际制动减速度曲线如图7所示,制动减速度指令曲线如图8所示。
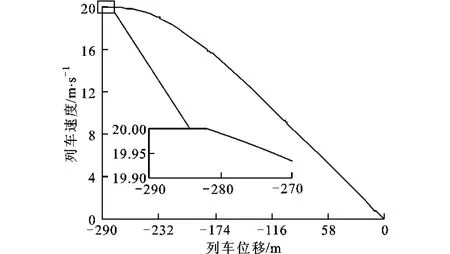
图6 列车实际停车曲线

图7 实际制动减速度曲线
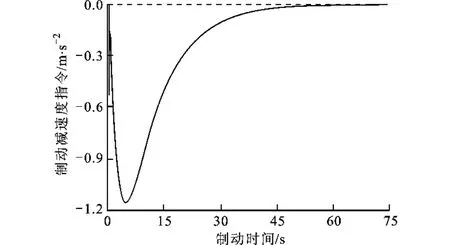
图8 制动减速度指令曲线
图7 显示,在整个制动过程中制动减速度的数值满足最大制动减速度的约束,且制动减速度曲线较为光滑,保障了列车运行的平稳性以及乘坐的舒适性。由于系统的输入时滞,实际制动减速度的响应存在0.4s延时。由图8可以看出,制动减速度指令同样满足最大减速度的约束,且制动过程中牵引单元不工作。随着列车的速度不断降低及向期望停车点不断靠近,控制器也不断调整制动减速度指令,且最终收敛于0,实现了自动停车功能。
4 结 语
本文根据电空制动系统的工作原理,建立了具有输入时滞的非线性城轨列车制动模型。该模型克服了传统模型中制动减速度难以测量的缺点,反映了电空制动系统的动态特性以及闸瓦摩擦系数的非线性。基于该模型并结合Krasovskii泛函算子设计了反推自动停车控制算法。这一算法的主要改进在于基于预测的思想和反推控制技术,将误差信号表示为2个与延时相关的Krasovskii泛函算子,并且其中一个泛函算子是指数收敛的。通过Lyapunov-Krasovskii定理,证明了闭环系统的稳定性和收敛性。利用Matlab/Simulink仿真软件对制动系统进行了数值仿真,结果表明:该算法不仅对系统中的延时和非线性具有良好的鲁棒性,从而可获得较高的停车精度,并且可以保障列车运行的平稳性。本文提出的控制算法对于自动停车控制器的设计与应用具有实际意义。
[1] 王月明.动车组制动技术 [M].北京:中国铁道出版社,2004:43-64.
[2] 唐涛,黄良骥.列车自动驾驶系统控制算法综述 [J].铁道学报,2003,25(2):98-102.
TANG Tao,HUANG Liangji.A survey of control algorithm for automatic train operation [J].Journal of China Railway Society,2003,25(2):98-102.
[3] YASUNOBU S,MIYAMOTO S,IHARA H.A fuzzy control for train automatic stop control[J].Transactions of the Society of Instrument and Control Engineers,2002,E-2(1):1-9.
[4] 余进,钱清泉,何正友.两级模糊神经网络在高速列车ATO系统中的应用研究 [J].铁道学报,2008,30(5):52-56.
YU Jin,QIAN Qingquan,HE Zhengyou.Research on application of two-degree fuzzy neural network in ATO of high speed train[J].Journal of China Railway Society,2008,30(5):52-56.
[5] CHANG C S,SIM S S.Optimising train movements through coast control using genetic algorithms [J].IEE Proceedings on Electric Power Applications,1997,144(1):65-73.
[6] SONG Qi,SONG Yongduan,TANG Tao,et al.Computationally inexpensive tracking control of high-speed trains with traction/brake saturation [J].IEEE Transactions on Intelligent Transportation Systems,2011,12(4):1116-1125.
[7] 罗仁士,王义惠,于振宇,等.城轨列车自适应精确停车控制算法研究 [J].铁道学报,2012,34(4):64-68.
LUO Renshi,WANG Yihui,YU Zhenyu,et al.Adaptive stopping control of urban rail vehicle [J].Journal of China Railway Society,2012,34(4):64-68.
[8] HUA Changchun,GUAN Xinping,SHI Peng.Robust backstepping control for a class of time delayed systems[J].IEEE Transactions on Automatic Control,2005,50(6):894-899.
[9] RICHARD J P.Time-delay systems:an overview of some recent advances and open problems [J].Automatica,2003,39(10):1667-1694.
[10]BEKIARIS N,KRSTIC M.Stabilization of linear strictfeedback systems with delayed integrators[C]∥Proceedings of American Control Conference.Piscataway,NJ,USA:IEEE,2010:6579-6584.
[11] MAZENC F,BLIMAN P.Backstepping design for time-delay nonlinear systems[J].IEEE Transactions on Automatic Control,2006,51(1):149-154.
[12]MAZENC F,NICULESCU S I,BEKAIK M.Stabilization of nonlinear systems with delay in the input through backstepping [C]∥Proceedings of the 50th IEEE Conference on Decision and Control.Piscataway,NJ,USA:IEEE,2011:7605-7610.
[13]YAMAZAKI H,MARUMO Y,IIZUKA Y,et al.Driver model simulation for railway brake systems[C]∥Proceedings of the 4th IET International Conference on Railway Condition Monitoring.Piscataway,NJ,USA:IEEE,2008:1-6.
[14]NANKYO M,ISHIHARA T,INOOKA H.Feedback control of brake deceleration on railway vehicle [J].ASME Journal of Dynamic Systems Measurement and Control,2006,128(2):244-250.
[15]KRSTIC M,KANELLAKOPOULOS I,KOKOTVIC P.Nonlinear and adaptive control design [M].New York,USA:Wiley,1995:21-86.
[16]GU K Q,KHARITONOV L,CHEN J.Stability of time-delay systems[M].Boston,USA:Birkhauser,2003:1-27.
[本刊相关文献链接]
俞珏,庄健,于德弘.采用李雅普诺夫函数的电液伺服系统反馈 线 性 化 控 制.2014,48(7):71-76.[doi:10.7652/xjtuxb 201407013]
许建,张政,李翔,等.独立驱动电动汽车横摆力矩的模糊控制算法.2014,48(7):83-89.[doi:10.7652/xjtuxb201407015]
邓飙,苏文斌,郭秦阳,等.双缸电液位置伺服同步控制系统的智能控制.2011,45(11):85-90.[doi:10.7652/xjtuxb2011 11016]
李大海,李天石.非均匀采样系统的支持向量回归建模与控制.2011,45(3):65-69.[doi:10.7652/xjtuxb201103012]
闫中江,沈中,常义林,等.一种修复网络拓扑的Steiner树移动控制算法.2011,45(2):39-43.[doi:10.7652/xjtuxb2011 02008]
张颖,沈中,常义林.一种信号强度感知的Ad Hoc网络节点移动控制算法.2011,45(2):107-110.[doi:10.7652/xjtuxb 201102022]
王科,刘新正.免疫单神经元PID控制在永磁交流伺服系统中的应用.2010,44(4):76-82.[doi:10.7652/xjtuxb2010040 17]
孟庆龙,王元,闫秀英.采用计算流体力学数值模拟的比例积分控制器.2009,43(5):90-93.[doi:10.7652/xjtuxb2009050 19]
王换招,董贝,罗韩梅,等.基于k-覆盖保证的异构传感器网络节点调度策略.2008,42(8):940-944.[doi:10.7652/xjtuxb 200808003]
方炜,姜长生.一类基于模糊系统的非线性鲁棒自适应预测控制.2008,42(6):669-673.[doi:10.7652/xjtuxb200806005]
李德军,张小栋,王云霞.轮式移动机器人行走的模糊比例积分控制 方 法.2008,42(1):126-128.[doi:10.7652/xjtuxb 200801029]
吕晓军,郑南宁.车辆单神经元模型参考自适应控制算法研究.2007,41(12):1391-1395.[doi:10.7652/xjtuxb2007120 02]
余向阳,杜小宁,田军伟,等.双模糊免疫比例积分微分下的水力发电机组调速器研究.2007,41(10):1229-1232.[doi:10.7652/xjtuxb200710023]
曹军义,曹秉刚.分数阶控制器离散方法的评估策略研究.2007,41(7):842-846.[doi:10.7652/xjtuxb200707020]
黄建辉,钱德沛,王胜灵,等.基于动态带宽预留和带宽降级的呼叫准入控制算法.2007,41(6):683-687.[doi:10.7652/xjtuxb200706012]
