内嵌晃荡液体减振的流固耦合分析

郭 涛，李国君

（西安交通大学热流科学与工程教育部重点实验室，710049，西安）

晃荡减振方法是指将部分充液的容器附加在弹性结构上，当弹性结构发生振动时，液体在容器内的晃荡与弹性结构相互作用，从而起到被动减振的效果，其基本结构如图1所示。该方法具有效果明显、结构简单、调节方便、适应性强等优点。Fujino等率先使用实验的方法研究了影响晃荡减振器的各项参数，得到了容器宽度越大、液体黏性越小、减振效果越好，且壁面摩擦对减振影响较小等多个结论［1］；Kaneko等采用数值的方法研究了方形晃荡减振器内液体晃荡的情形［2-3］；Anderson等通过在深水减振器中加入横截梁制造浅水晃荡的方法提高了减振能力［4］；Marsh等研究了浅水晃荡减振下液体深度与容器宽度对减振效果的影响，认为行进波的能耗作用远大于驻波，因此行进波的晃荡减振效果优于驻波晃荡［5］；徐晖等利用实验、数值计算等手段研究了内嵌式晃荡减振对悬臂梁振动衰减的影响，认为悬臂梁内的内嵌晃荡单元的减振因素包括附加质量调频、黏性耗散、液体阻碍等［6-9］。

在实验中，内嵌流体在不同的结构中取得的减振效果差异明显，甚至不当的参数还会对振动起到激励的作用［4，7］。目前，关于晃荡流体减振的理论分析仍没有统一的结论：国外研究通常认为［1，5］，在自由晃荡频率与系统振动频率相似的情况下，晃荡减振效果最好，且浅水行进波的减振能力远大于深水驻波，但对不同的容器宽度，最理想的水深有所不同；徐晖等认为［8-9］，在内嵌式晃荡减振器中，液体的附加质量调频效应及吸能效应对减振的影响最大，其次是运动液体对梁运动的阻碍作用力。这些结论都得到了实验及数值计算结果的支持，但在指导晃荡减振器的参数选择时仍有不足，难以达到最优结果。本文采用分离求解器隐式耦合的方法，模拟了内嵌式晃荡减振器在悬臂梁一阶振动中的作用，并从液体的受迫晃荡机理出发，探讨了内嵌流体造成振动衰减的内在原因，目的是为优化选择晃荡减振器的参数提供理论依据。

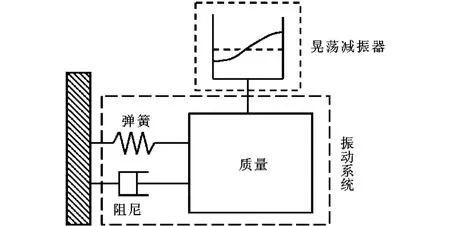
图1 晃荡减振器的基本结构

1 物理模型与数值方法

1.1 物理模型

仿照徐晖等的实验［6］，构建了内嵌晃荡流体的悬臂梁的物理模型，其结构如图2所示。铝合金梁的内部空腔中注入了部分液体，使腔内为气-液两相流体状态，梁静止时液体静止在腔下部，梁振动时液体受迫晃动并起到减振的作用。悬臂梁尺寸为600 mm×12mm×30mm，空腔尺寸为550mm×8mm×8mm且距离梁自由端20mm，充液比例为50%，悬臂梁的一阶固有频率约为22Hz。在梁的自由端施加一个22Hz的正弦激励载荷，或施加一个初始位移，梁将做受迫或自由衰减振动，这样便可观察内嵌晃荡减振器的悬臂梁的瞬态响应。

图2 内嵌晃荡流体的悬臂梁结构

图3 耦合方法在单位时间步内的计算流程

1.2 数值计算方法与两相流模型

在悬臂梁内置晃荡减振器后的瞬态响应中，悬臂梁的振动与内嵌液体的晃荡相互影响，是一个流固耦合过程。本文使用分离求解器交错迭代的隐式耦合方法进行数值模拟，该耦合方法在单位时间步内的计算流程如图3所示。固体域使用有限元法离散求解应力-应变矩阵方程，流体域使用有限体积法离散求解Reynolds-Averaged Navier-Stokes方程；分离求解器分别将计算结果（流体域解得液体对梁的作用力，固体域解得梁内壁的位移）作为另一域求解的新边界条件；在一个时间步内的循环次数由收敛条件及最大迭代次数决定。本方法具有以下优势：在每个时间步内流体域及固体域均存在未知量，隐式耦合求解可保证计算在时间积分上守恒；在不求解两域联立统一矩阵的情况下，交错迭代能得到相似的计算精度且降低了计算难度；面对不同的耦合问题，可以针对性地采用不同的单域求解器，以保证计算的稳定性与灵活性。

计算的时间步长为梁振动周期的1／200，计算总时间为0.4s。计算固体域时，铝合金与有机玻璃侧窗紧密连接，按固体材料设置相应的物性；悬臂梁以一阶固有频率横振动时，阻尼系数ξ约为0.034 5；考虑梁变形较大时刚度变化引起的非线性因素，设悬臂梁内腔壁面为流固耦合的交界面。计算流体域时，网格变形使用位移扩散模型；平流项离散采用高分辨率差分格式，瞬态项离散采用二阶向后欧拉算法；收敛精度为10-5，每一时间步内最多交叉迭代10次。计算精度为双精度，以避免计算自由表面曲率时存在较大的舍入误差。本文定义气-液两相均为连续相，同时采用基于密度差异的浮力模型、谐波平均方法，以避免交界面上气相出现伪速度；采用非均质的自由表面流动模型，以便于将一相流体飞溅到另一相后可以重新分离；采用标准κ-ε模型计算均质化的湍流场，以避免计算发散；采用连续表面张力模型、体积加权的体积分数进行光顺；采用流体曳力模型计算相间的动量传递，曳力系数取0.44；采用耦合法计算两相的体积分数。

2 数值计算结果及分析

2.1 悬臂梁的瞬态响应

流体及固体域求解时均采用六面体结构化网格，为验证计算精度及网格无关性，采用3种不同密度的网格分别进行计算，并基于弹性系统振动响应的数值解及解析公式得到固有圆周频率Pd、阻尼系数ξ及受迫振动的稳态振幅衰减率Ra。不同网格数下计算结果及计算消耗的对比如表1所示。由表1知：3种网格下Pd、ξ和Ra的结果相近，说明本文采用的网格密度对于悬臂梁减振性能的预测影响不大；Ra的实验值为65.9%［6］，与计算结果偏差较小，证实了本文数值计算的精度；随着网格数的增加，CPU时间tCPU成比例增加，考虑时间消耗，在随后的数值计算中采用第1种网格进行数值模拟。

表1 不同网格数下计算结果及计算消耗对比

加入晃荡流体前后悬臂梁自由端的瞬态响应对比如图4所示。从图4中可见，无论是自由振动还是受迫振动，嵌入晃荡减振器后悬臂梁的振动均得到抑制。由图中悬臂梁瞬态响应的数值解可以得到：梁的一阶自由振动频率约为22.03Hz，ξ约为0.033，与解析值略有差异，这可能是梁非线性变形的影响所致；加入了晃荡减振器后，梁的自由振动频率减小，约为21.65Hz，ξ增大，约为0.048，这说明晃荡减振器同时改变了梁的自由振动频率及阻尼。自由振动衰减的主要因素是阻尼增大，除此之外，受附加液体质量等因素影响而改变的梁的自由振动频率也会抑制原梁固有频率激励下的受迫振动的振幅。

图4 加入晃荡流体前后悬臂梁自由端的瞬态响应对比

2.2 晃荡减振器的原理

一个振动周期内流体晃荡作用力与梁偏转相位的关系如图5所示。从图5中可见：流体对梁的作用力与正弦曲线相似；无论是梁的自由振动还是受迫振动，两相流体对梁的作用力均滞后于梁自身位移的相位。这种滞后造成了梁的运动方向与流体作用力方向相反的时间比方向相同的时间长。由牛顿第二定律：力与梁运动方向相同时产生激励冲量加剧振动；力与梁运动方向相反时产生阻尼冲量抑制振动。图5中受力曲线与0值水平线所围面积为冲量，其中阴影部分为阻尼冲量，白色部分为激励冲量，阴影面积远大于白色面积。可见，流体晃荡作用力的滞后造成了其对梁的阻碍作用大于激励作用，这是晃荡减振的直接原因。

图5 一个振动周期内流体晃荡作用力与梁偏转相位的关系

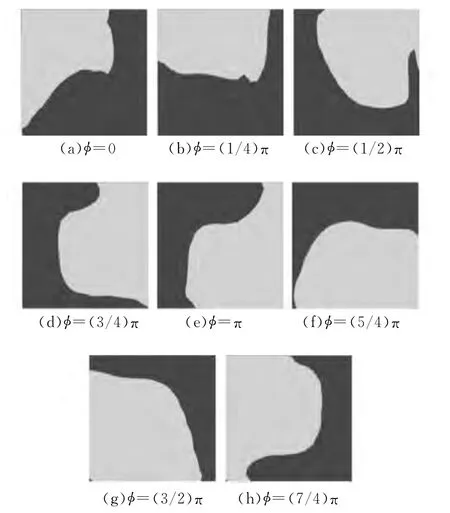
图6 距离悬臂梁自由端25mm处晃荡减振器内在一个振动周期的自由表面变化

从能量角度看：若梁的受力曲线保持简谐形状且与自由端位移曲线在相位上保持同步，则说明梁带动液体晃荡，或液体带动梁振动，能量转化只是在液体的机械能与梁的机械能之间进行，能量的衰减来自于液体剪切流动引发的黏性耗散及梁自身的阻尼耗散；若梁的受力曲线在相位上滞后于自由端位移曲线，则说明梁带动液体晃荡，梁在将部分机械能传递给液体后，由于运动方向提前改变而需要继续消耗机械能来消除液体的阻碍，并继续带动液体晃荡，此时能量通过梁与液体的冲撞不断地转化为两者的内能，这样能量的衰减速度大大提高；若梁的受力曲线在相位上提前于自由端位移曲线，则液体的机械能不断转化为梁的机械能，液体引发并加剧了梁的振动。假设梁的受力曲线保持简谐形状，晃荡力滞后1／4周期时液体始终阻碍梁振动，此时减振效果最好；反之，若晃荡力提前1／4周期时液体始终激励梁振动。

距离悬臂梁自由端25mm处晃荡减振器内在一个振动周期的自由表面变化如图6所示。从图6中可见：气液分界面及液体质心随梁的位移相位φ的变化而不断变化，当梁在振动平衡位置且具有最大振动速度时（见图6a或6e），液体明显偏离平衡位置且聚集在梁振动速度的相反方向上，此时相对速度较小；当梁振动速度逐渐减小时，梁内液体由于梁对其做正功而加速（见图6b或6f），液体质心不断远离梁振动速度负向上的壁面而向正向壁面移动，液体质心继续移动且通过相对平衡位置，此时液体对梁的作用力反向，相对速度在最大值附近；当梁达到最大位移（见图6c或6g）时，部分液体冲击侧壁并沿侧壁运动到达顶壁（或底边），但还未达到最大相对位移，此时相对速度减小；当梁速度反向且继续向平衡位置移动 （见图6d或6h）时，液体在侧壁附近，此时相对速度的方向开始反向，液体通过侧壁直到梁再次经过平衡位置。液体的相对运动受流固耦合影响而不再具有完全对称性，但仍具有一定的周期性。可见，液体对梁的作用力滞后是液体晃荡滞后引起的。

3 液体自由晃荡对梁振动的影响

液体的晃荡位移相对于梁的振动具有滞后性，致使梁振动受到抑制。液体在简谐激励下的晃荡可认为是液体进行稳态的简谐受迫晃荡与液体在变加速度下进行瞬态自由晃荡共同作用的结果。液体的稳态受迫晃荡与外界激励具有同步性，不会产生滞后，实际上液体晃荡的滞后是由伴随的自由晃荡产生的。液体在容器内偏离了势能最低的位置后会产生自由晃荡，如果液体的自由晃荡频率低于容器摇摆频率，则当容器达到最大位移且速度开始反向时，壁面附近的液体受到壁面约束而与容器保持同步，而远离壁面的液体则受自由晃荡影响后的相对速度仍未反向，所以液体的整体晃荡相位将滞后于容器。反之，如果液体的自由晃动频率高于容器摇摆频率，则当容器达到最大位移之前液体先贴近壁面并受到约束，所以液体的整体晃荡相位将与容器摇摆相一致，此时减振容器的摇摆频率即为固体振动频率。由此可见，造成振动衰减的液体滞后效应是由自由晃荡频率低于固体振动频率产生的。液体的一阶自由晃荡具有最大的质量偏移，其造成的能量耗散最多，因此本文只考虑一阶自由晃荡频率对减振的影响。

在简谐水平激励下，内嵌晃荡液体势能的最低位置不断变化，此时晃荡剧烈，能量衰减快，这样瞬变的自由晃荡频率难以直接考察。为此，本文提出采用时均加速度下液体的驻波频率来代替液体的自由晃荡频率，并使用固体振动频率与驻波频率的比值γ的方法间接地考察自由晃荡对振动的影响。液体晃荡是自由表面波传播的过程，当外在加速度固定不变且波幅远小于水深及波长时，表面波到达壁面后会形成反射波，并与原来的波经叠加形成驻波，即自由晃荡以固定频率小波幅进行。简化模型的驻波圆周频率解析解如下

式中：a为等效合加速度；B为等效容器宽度；d为等效水深；i为驻波阶数。忽略容器形状、晃荡幅度等因素的影响，假设时均加速度下的驻波频率为液体在相同加速度下的瞬时自由晃荡频率。当γ=1、简谐加速度的瞬时值小于时均值时，液体瞬时自由晃荡频率小于振动频率，液体晃荡滞后。尽管液体的实际瞬时自由晃荡频率受诸多因素的影响，其与驻波频率的比例关系并不固定，但驻波频率确实在液体自由晃荡频率的变化范围内。对于确定的晃荡减振器，γ可以作为衡量液体滞后现象发生的量度：γ值越大，振动频率将在更多的时间内大于液体瞬时自由晃荡频率，晃荡液体的滞后现象越明显，液体阻尼冲量所占的比例就越大；在晃荡强度相同的情况下，相同质量的液体对固体振动的衰减效应越强。因此，γ较大，意味着晃荡液体的滞后及减振能力较大。下面用2个数值模拟的算例来验证γ的参考作用。算例1 薄片方形容器内拥有一阶驻波频率为5Hz的水，质量为1g，容器分别以2.5Hz、10Hz的简谐频率振动，振幅恒定为5mm，此时考察γ分别为0.5、2.0时液体晃荡对容器的作用力。假设在等振幅晃荡的3～5个周期，内嵌水的受迫晃荡趋于稳定。此区间内嵌水对容器的作用力与容器振动相位的关系如图7所示。

图7 内嵌水对容器的作用力与容器振动相位的关系

从图7中可见：当容器以2.5Hz频率振动时，容器振动频率低于时均加速度下的驻波频率，容器的受力曲线相位相对于容器位移相位时前时后，此时晃荡对容器壁面的总冲量约为1.039 6×10-3N·s，其中激励冲量约为4.964×10-4N·s，抑制冲量约为5.432×10-4N·s，净抑制冲量占总体的4.5%，显然减振效果不好；当容器以10Hz频率振动时，容器振动频率高于时均加速度下的驻波频率，受力曲线相位基本上落后于容器位移相位，第4周期的相位差尤较大，此时晃荡对容器壁面的总冲量约为2.843×10-3N·s，其中激励冲量约为1.213×10-3N·s，抑制冲量约为1.63×10-3N·s，净抑制冲量约占总体的14.65%，显然减振能力增强。这证实了较大的γ更容易造成液体晃荡相位滞后，从而减振效果得以增强。

算例2 在悬臂梁内嵌入3种不同大小的减振器，通过改变充液比例或悬臂梁尺寸使γ发生变化，以此模拟悬臂梁自由衰减振动过程，同时用等效阻尼系数ξeq来考察减振器内单位质量液体的减振能力

式中：ξt为梁内置减振器后的整体阻尼系数；ξs为悬臂梁自身阻尼系数；Qw、Qb分别为晃荡液体与悬臂梁的质量。数值模拟的参数与计算得到的减振效果如表2所示。从表2结果可见，3种不同的晃荡减振器中，ξeq均随着γ的增加而增大，这佐证了随着γ的增大，液体的晃荡滞后效应增强，相同质量的液体可以产生更多的阻尼冲量。

在设计或优化内嵌式晃荡减振器时，相较于数值模拟方法，γ计算简单、易行，是一个设计参考依据，但不能用于不同晃荡减振器之间的横向比较，仅可作为设计或优化已知晃荡减振器中某一项参数时的参考依据。表2中的数据也证实了这一点。

表2 不同γ下3种减振器的减振能力对比

4 结 论

内嵌式晃荡减振除了流体黏性耗散、附加质量改变固有频率等因素外，内部液体的相对运动，即受迫晃荡滞后于梁的振动，也是造成液体阻尼冲量大于激励冲量的主要原因。滞后现象越明显，阻尼冲量的比例越大，液体晃荡的减振效果越强。液体受迫晃荡时受自由晃荡频率的影响，自由晃荡频率小于振动频率将造成受迫晃荡滞后。简谐加速度激励下液体瞬时自由晃荡频率难以预测，其对受迫晃荡滞后的影响可以用振动频率与时均加速度下的驻波频率的比值γ来考察。用数值模拟的方法分析固定频率晃荡的方形容器内液体的作用力，以及内置不同尺寸减振器的悬臂梁自由衰减振动，都证实了一个较大的γ值有助于提高单位质量晃荡液体的减振能力，该方法可为晃荡减振器的参数设计与优化提供参考。

［1］ FUJINO Y，PACHECO B M，CHAISERI P，et al.Parametric studies on tuned liquid damper （TLD）using circular containers by free-oscillation experiments［J］.Struct Engrg／Earthquake Engrg，1988，5（2）：177-187.

［2］ KANEKO S，YOSHIDA O.Modeling of deepwatertype rectangular tuned liquid damper with submerged nets［J］.Journal of Pressure Vessel Technology，1999，121（4）：413-422.

［3］ YAMAMOTO K，KAWAHARA M.Structural oscillation control using tuned liquid damper［J］.Computers ＆Structures，1999，71（4）：435-446.

［4］ ANDERSON J，SEMERCIGIL S，TURAN Ö.An improved standing-wave-type sloshing absorber ［J］.Journal of Sound and Vibration，2000，235（4）：702-710.

［5］ MARSH A，PRAKASH M，SEMERCIGIL E，et al.A shallow-depth sloshing absorber for structural control［J］.Journal of Fluids and Structures，2010，26（5）：780-792.

［6］ ZHANG X，LI J，XU H，et al.Numerical study of self-adaptive vibration suppression for flexible structure using interior inlay viscous fluid unit method［J］.Journal of Sound and Vibration，2006，297（3）：627-634.

［7］ 黄志祥，徐晖，徐立勤.内嵌黏性流体欧拉梁的自适应减振模式研究 ［J］.西安交通大学学报，2006，40（9）：1099-1103.

HUANG Zhixiang，XU Hui，XU Liqin.Adaptive vibration suppression mode for Euler beam with interior inlay viscous fluid［J］.Journal of Xi’an Jiaotong University，2006，40（9）：1099-1103.

［8］ JING D，XU H，WANG X.Experimental study of self-adaptive remnant vibration suppression for flexible structure with interior inlay viscous fluid unit ［J］.Journal of Vibration and Control，2011，17（12）：1886-1892.

［9］ JI C，XU H，XU L.Simulation and experiment of adaptive vibration suppression mode of plate with imbedded viscous fluid units［J］.Mechanical Science and Technology for Aerospace Engineering，2007，26（9）：1130-1134.