薄衬层结构滑动轴承润滑膜厚度的超声检测方法

耿 涛，孟庆丰，贾 谦，张 凯，袁小阳

（西安交通大学现代设计及转子轴承系统教育部重点实验室，710049，西安）

滑动轴承广泛应用于高速、精密、重载等场合，并已成为大型火电、水电机组、核电站主循环泵、高速精密机床等设备中的重要核心部件。流体润滑滑动轴承是依靠流体润滑膜将轴瓦和轴颈表面隔开的，其润滑膜的特性和状态决定了滑动轴承的承载能力、运行平稳性和寿命等运行能力，因此对流体润滑膜厚度等状态的检测无论是对于流体润滑理论的实验对比研究，还是对于滑动轴承的运行状态监测，都具有重要意义。同时，滑动轴承流体润滑膜存在于相对运动的两界面间，厚度通常在亚微米级到数十微米级之间，并具有实时变化的特点，这些使得流体润滑膜厚度的检测具有很大的挑战性。

相对于传统电阻法、电容法等润滑膜厚度检测方法，超声波检测方法无需对摩擦副表面进行改动，其具有的穿透能力也弥补了光学方法要求透光性的不足，因此基于超声波技术的检测方法对于真实工况滑动轴承润滑膜厚度的检测具有明显的优越性。Dwyer-Joyce等根据中间介质层刚度与超声波反射系数的关系，引入了润滑膜厚度的超声波刚度模型测量法［1-2］，将中间流体层厚度的超声波测量范围扩展到十微米至亚微米的量级，为润滑膜厚超声波检测的实际应用奠定了理论基础［3-4］。

超声波刚度模型测量法给出了轴瓦-流体膜-轴颈3层结构情况时润滑膜厚的具体测量方法［5-6］。然而，通常滑动轴承轴瓦由基体和衬层两部分通过浇铸或轧制形成，如图1所示，衬层厚度通常在不足1mm到6mm范围内，这样，在保证超声测厚法原有不破坏轴承结构优越性的前提下，3层结构的测量模型就变成了轴瓦基体-衬层-流体膜-轴颈4层的结构形式。以短脉冲超声波测量为例，通常超声波在被测材料内占有3个波长以上的脉冲宽度，当频率为10MHz的超声波入射钢-巴氏合金结构的轴瓦时，超声波在巴氏合金层的脉冲宽度约为1mm，而当采用5MHz的长脉冲换能器时，这一宽度值变为4.6mm，当轴瓦衬层厚度小于这一脉冲宽度的一半时，超声波脉冲在4层结构测量模型的第一和第二界面的反射回波就会发生叠加现象，这即是本文中“薄衬层”的含义。厚衬层与薄衬层轴瓦超声反射回波信号分别如图2、图3所示，其中，Pb为轴瓦基体 -衬层界面回波，P1、P2、P3等分别为衬层 -流体膜界面回波在衬层间的反复透射、反射形成，Pm则为薄衬层情况时以上各次回波的叠加信号。当反射回波发生叠加时，就无法再利用原有的刚度模型法得到轴瓦-流体膜界面的反射系数，因此难以直接将该方法使用到多数情况下滑动轴承润滑膜厚度测量的实际工程应用中。

本文根据时域叠加信号的频谱分析方法，对薄衬层情况时轴瓦衬层-流体膜界面的含有膜厚信息的反射回波与轴瓦基体-衬层界面反射回波相叠加的信号进行频域分析，提取出回波中与流体膜厚度变化有关的信息，进而得到流体层界面反射系数与润滑膜厚度值；建立了多次回波信号相叠加的具有薄衬层结构滑动轴承润滑膜厚度的超声波刚度模型测量方法，并通过实验对该方法进行了验证。

图1 具有合金衬层结构的径向与推力滑动轴承轴瓦

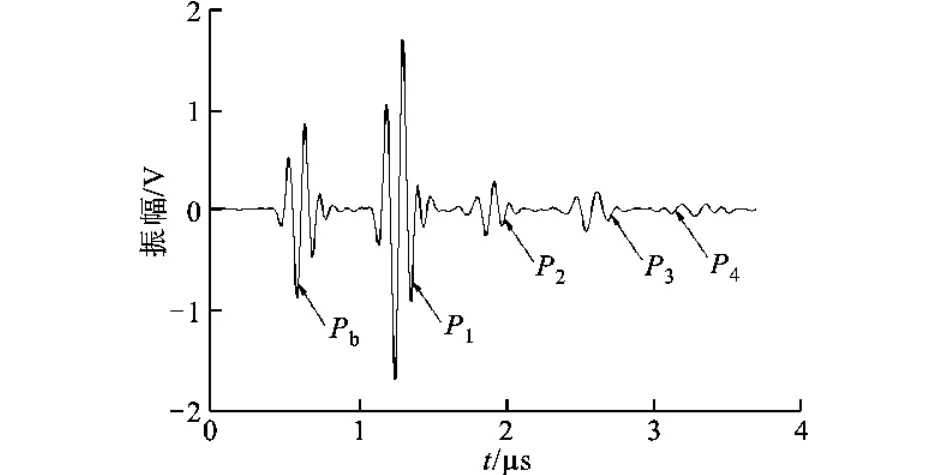
图2 厚衬层轴瓦超声反射回波信号

1 刚度模型法膜厚测量

刚度模型法适用于流体润滑膜厚度远小于所用超声波波长的情况，当介质层厚度远小于超声波波长时，该介质层刚度K决定了入射波经过该介质层时的反射系数

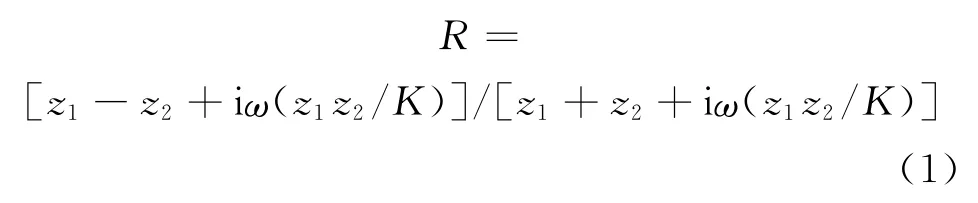
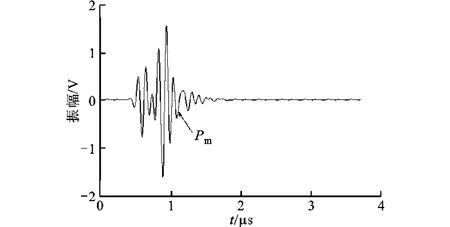
图3 薄衬层轴瓦超声反射回波信号

式中：z1、z2分别为该介质层隔开的两侧物质的声阻抗；ω为超声波角频率。

介质层刚度表示为厚度方向的单位改变量所需要的压力，即K=-dp／dh。对于流体润滑膜层所在的尺度，认为流体膜体积的变化只发生在厚度方向，这样，流体膜体积模量表示为B=-dp／（dh／h）。由以上两式可得K=B／h。另外，液体中的超声波声速由该液体密度ρ和体积模量B决定，表示为c=（B／ρ）1／2。这样，由上面两式可以得到流体层刚度与该流体层介质参数之间的关系为K=ρc2／h。将此式带入式（1），并整理得到润滑膜层厚度与反射系数以及各层材料介质参数之间的关系为

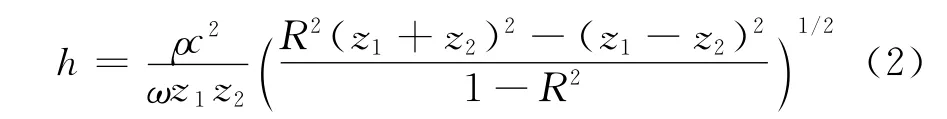
在式（2）中，润滑膜两侧所对应的轴瓦材料z1、轴颈材料z2以及流体层密度为已知量，这样，只要得到超声入射波经过润滑膜层后的反射系数，就可确定润滑膜的厚度。图4为根据式（2）得到的巴氏合金-油膜-钢介质膜厚与反射系数的关系曲线。由于超声波在轴瓦-空气界面的反射系数接近于1（轴瓦为钢时R=0.999 982，轴瓦为巴氏合金时R=0.999 961），因此需要首先得到测点处轴瓦-空气界面时的反射回波作为参考回波信号，然后将实际膜厚检测时得到的回波信号幅值与参考回波信号幅值相比，得到近似的反射系数，再由式（2）得到膜厚值。

2 回波信号叠加时的膜厚分析

对于3层结构的润滑膜厚检测模型，通过对回波信号进行傅里叶变换，将其幅度值与参考回波信号的幅度值进行比较，就可以得到式（2）中所需的回波反射系数。对于4层结构时相叠加的时域回波信号，由于膜厚的改变不影响轴瓦基体-衬层界面的回波幅度，即在不同膜厚测量中得到的叠加回波信号中的pb成分是固定不变的，是由材料参数决定的。这样，求出叠加回波信号中含有膜厚信息的衬层-流体膜界面回波成分与pb的幅值比，再得到衬层-空气界面回波与pb的幅值比作为参考幅值比，由以上两个与pb的幅值比就可以确定不同膜厚时的反射系数，从而得到膜厚值。

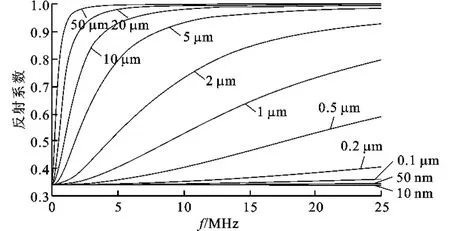
图4 巴氏合金-油膜-钢介质时膜厚与反射系数关系曲线

对于叠加脉冲信号的频域分析，以时间间隔为2t0的两个矩形脉冲信号f1（t+t0）和f2（t-t0）为例，并且f2的幅度为f1的k倍，设f1（t）的傅里叶变换为F（ω），按照傅里叶变换相关定理，可得叠加脉冲信号频域幅值为［7］

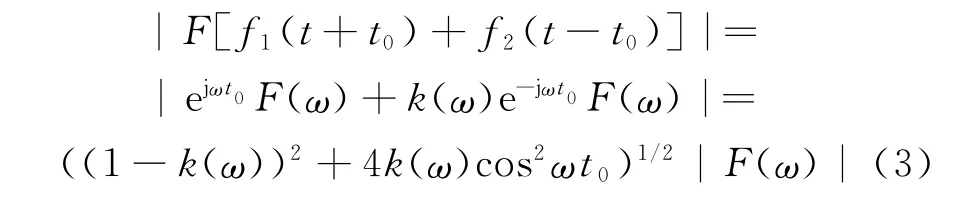
式中：k（ω）为频域中不同频率处两个脉冲信号的幅值比。

对于薄衬层时润滑膜厚的超声波检测，叠加回波信号pm（t）是由基体 -衬层界面回波信号pb（t）和衬层 -润滑膜界面的多次反射回波信号p1（t）、p2（t）、p3（t）等叠加而成，这些回波间的时间间隔均由衬层厚度与其材料属性决定，设超声波通过衬层厚度所用时间为t0，则往返合金衬层所形成的回波间的时间间隔为2t0。由于第一和第二界面材料参数的不同，以及不同润滑膜层厚度对第二界面回波幅度的影响，使得p1（t）与pb（t）有了一定的幅度差，而p1（t）、p2（t）、p3（t）等回波间的幅度差是由于经过合金层次数的不同所产生的不同衰减而形成的。首先，忽略p2（t）、p3（t）等回波对pm（t）的影响，设pm（t）由时间间隔为2t0的两个回波信号pb（t+t0）和p1（t-t0）形成，并设基体-衬层界面回波信号pb（t）的傅里叶变换为Pb（ω），则

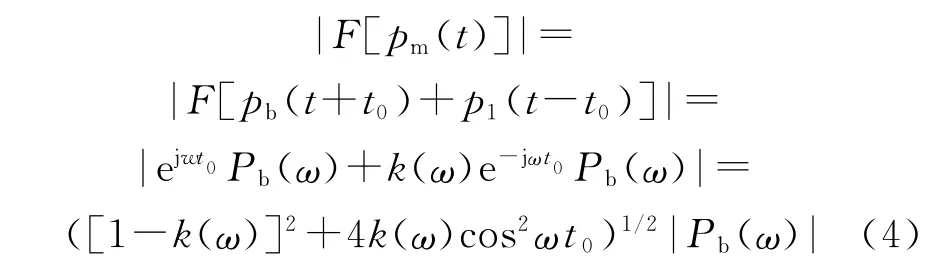
式中：k（ω）为频域中不同频率处两个脉冲成分的幅值比。于是，pm（t）与pb（t）在频域中的幅值比

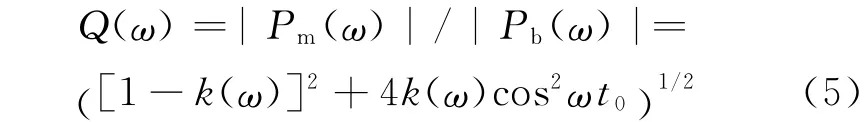
如果能事先得到|Pb（ω）|，则可以通过薄衬层回波pm（t）的幅值谱与|Pb（ω）|之比得到Q（ω），然后通过求解式（5）得到不同膜厚时p1（t）与pb（t）的频域幅值比k（ω），然后与衬层-空气界面得到的参考幅值比进行比较，从而得到反射系数与膜厚值。这样，就需要在进行薄衬层润滑膜厚检测前，通过加工相同材料的厚衬层轴瓦试块，并使用相同的超声检测系统，得到基体-衬层界面回波pb，如图2所示，这通常是容易实现的，也可通过材料声学参数的理论计算得到|Pb（ω）|，而若由相近材料的厚衬层轴瓦代替得到的pb，会影响最终膜厚测量结果的准确度，但并不影响对膜厚变化趋势的监测。得到Q（ω）后，式（5）变为含有k（ω）的方程

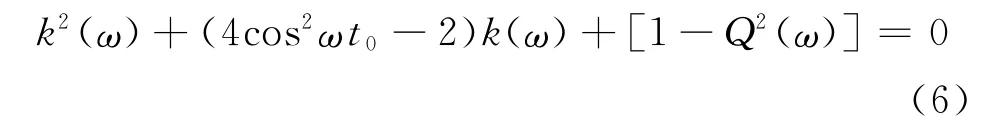
而由式（5）可知，Q（ω）是随频率按余弦方式波动的正值曲线，设在超声波回波中心频率附近处Q（ω）的峰值为Q（ωs），ωs为Q（ω）的峰值频率，则上式变为

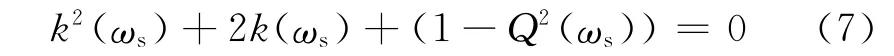
由式（7）可求出不同膜厚测量时含有膜厚信息的p1（t）与保持不变的pb（t）在ωs频率处的幅值比k（ωs）。同理，由事先检测的薄衬层轴瓦-空气界面的参考回波信号pm（t），根据式（5）、式（7）可得到空气界面时p1（t）与pb（t）在ωs频率处的幅值比ka（ωs），则不同膜厚时回波在ωs处的反射系数为

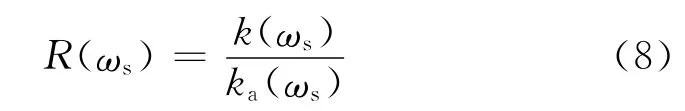
事实上，pm（t）中p2（t）、p3（t）等回波成分对|Pm（ω）|和Q（ω）的幅值有微小的影响，而同时所求取的ka（ωs）也包含在衬层-空气界面中多次回波p2（t）、p3（t）等的影响，而最终的比值R（ωs）则消减了这部分因素对于最终膜厚结果的影响。这样，求得R（ωs）后，根据式（2）就得到了薄衬层滑动轴承润滑膜厚度结果。

此外，在求取膜厚过程中所得到的式（5）中，曲线Q（ω）按余弦方式波动的频率与t0有关，而t0则是由薄衬层的厚度决定的，这样由Q（ω）得到的t0是判断薄衬层厚度的一种方法。式（5）右端两个极大或极小值点间的频率间隔为

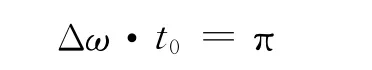
其中Δω=2πΔf，则

3 润滑膜厚检测实验

为了检验薄衬层轴瓦润滑膜厚检测方法的正确性，设计膜厚模拟装置，应用带有闭环控制的高精度压电致动器模拟不同厚度的润滑膜层，将超声波膜厚检测结果与压电致动器反馈结果进行比较，从而对超声检测方法进行检验。闭环压电致动器分辨力为2nm，最大行程为90μm，均满足测量结果检验和刚度模型法测量范围要求。图5为润滑膜厚模拟装置与检测系统，将薄衬层轴瓦固定在实验装置的底座上，以0.5mm厚巴氏合金衬层的滑动轴承进行实验验证，实验中采用10MHz超声波换能器。

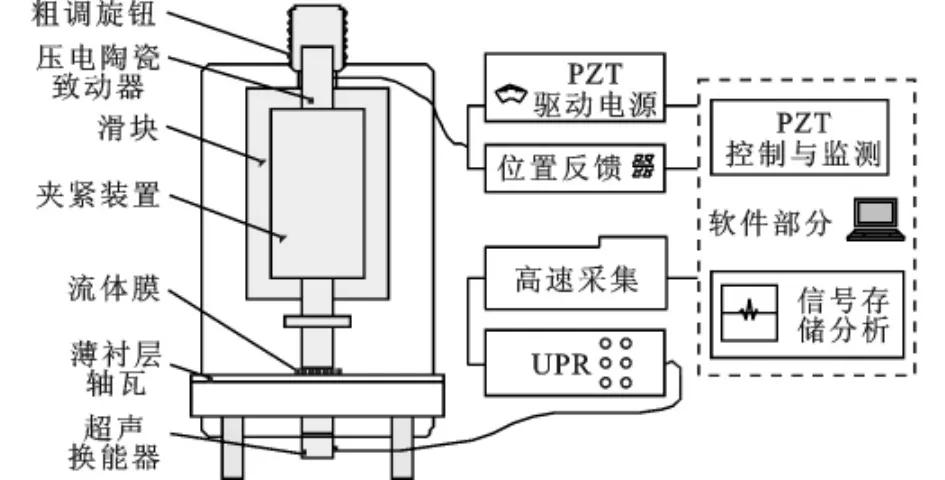
图5 润滑膜厚模拟装置与检测系统

首先，由厚衬层巴氏合金试块得到的|Pb（ω）|如图6所示，其时域波形pb（t）如图2中Pb所示。其次，测量所要检测的薄衬层滑动轴承在巴氏合金-空气界面时的参考回波信号，以及在不同润滑膜厚时的回波信号pm（t），参考回波信号以及部分膜厚的回波信号如图7所示，图中的设置膜厚即为闭环压电致动器读数显示的膜厚值。然后，对参考回波信号和不同膜厚的回波信号进行快速傅里叶变换，如图8所示，并按式（5）与图6所示的|Pb（ω）|相比，得到如图9所示的比值Q（ω）曲线。由图可见，在不同频率处出现了极大值与极小值，两个极小值点的频率差为3.32MHz，由式（9）可得t0为0.150 6μs，从而由巴氏合金纵波声速与t0之积得到衬层厚度为0.5mm，这与实际相符。

得到Q（ω）比值曲线后，由式（7）可得不同厚度润滑膜时的k（ωs）值如图10所示，图中不同符号表示多次测量。同理，由参考回波的Q（ω）值得到的参考回波ka（ωs）值如图11所示，其峰值频率ωs为10.4MHz，而由图9可见，不同膜厚时在中心频率10MHz附近的ωs并非与参考回波的ωs完全重合，这样为了得到准确的不同膜厚时峰值频率ωs处的反射系数，由式（6）确定参考回波在其ωs附近频率段的k值，5次测量结果显示在这一频率段参考信号衬层-空气界面回波成分与|Pb（ω）|有较稳定的k值。

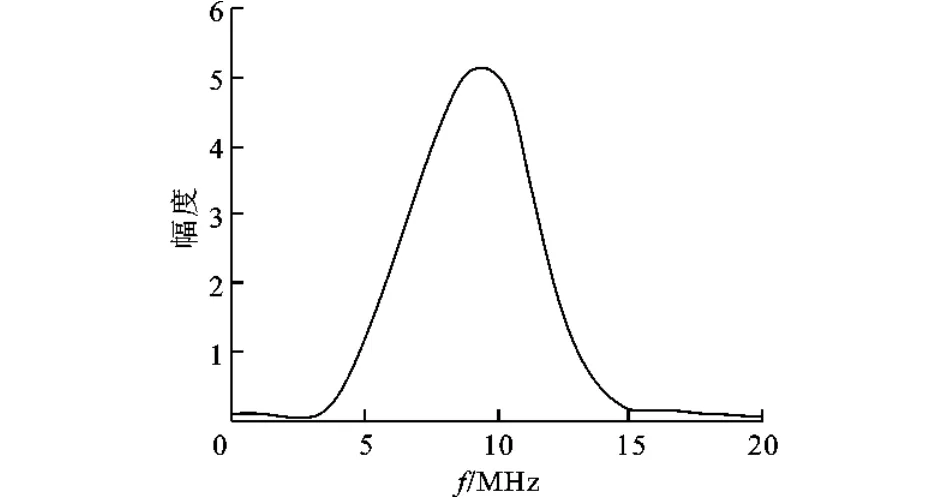
图6 基体-衬层界面回波信号幅值谱

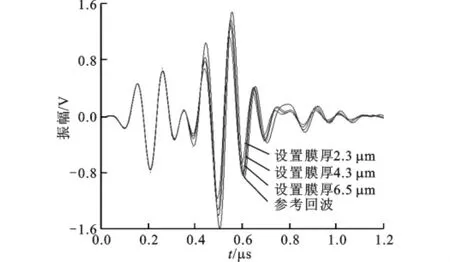
图7 参考回波和不同膜厚时的叠加回波时域信号

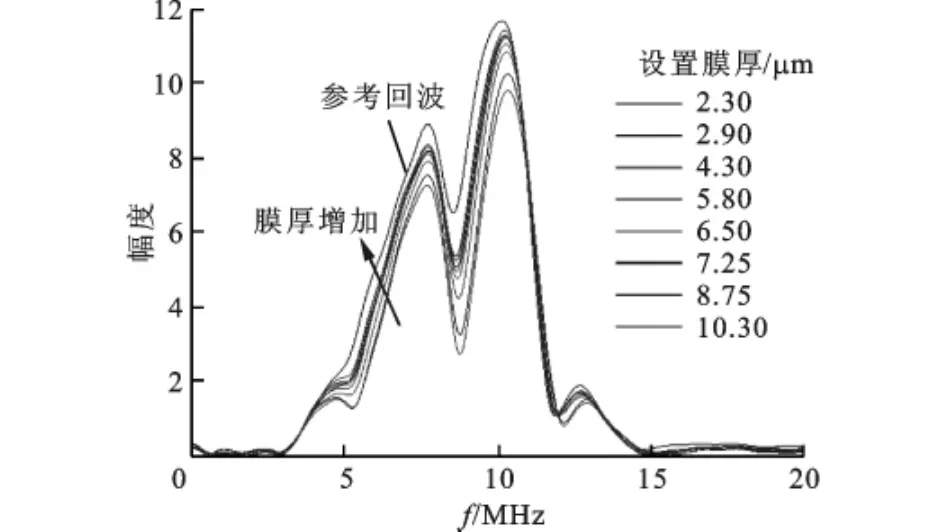
图8 参考回波和不同膜厚时叠加回波信号幅值谱

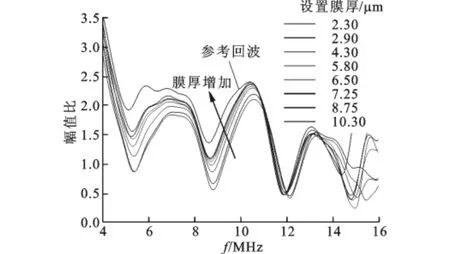
图9 参考回波和不同膜厚时叠加回波信号与基体-衬层界面回波幅值比

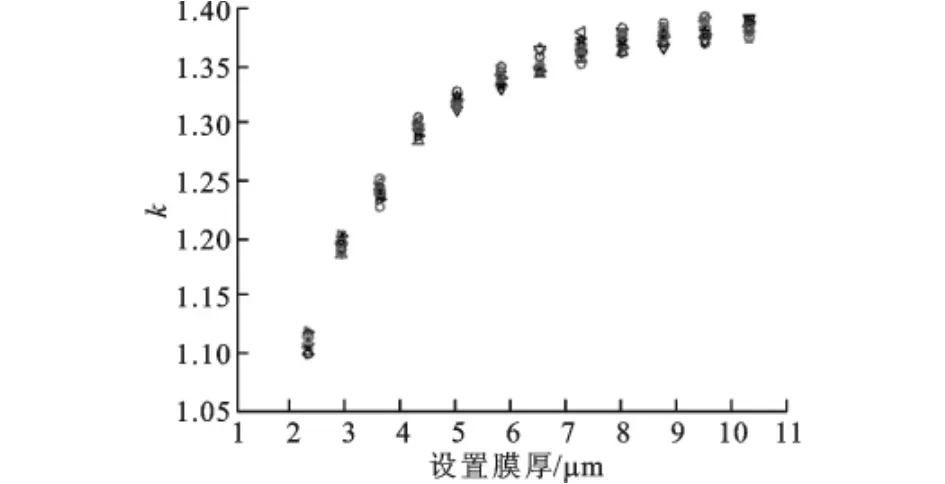
图10 不同膜厚时衬层-润滑膜界面回波与基体-衬层界面回波幅值比

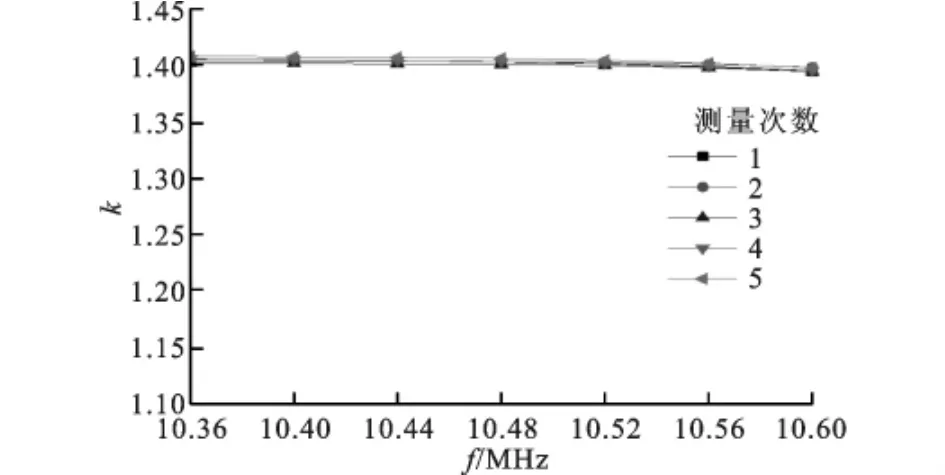
图11 参考回波信号衬层-空气界面回波与基体-衬层界面回波幅值比

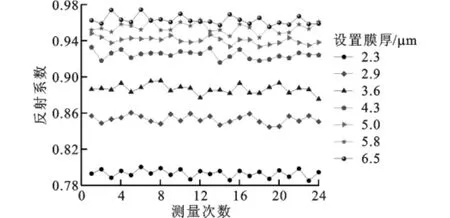
图12 由k值得到的不同膜厚时的反射系数值

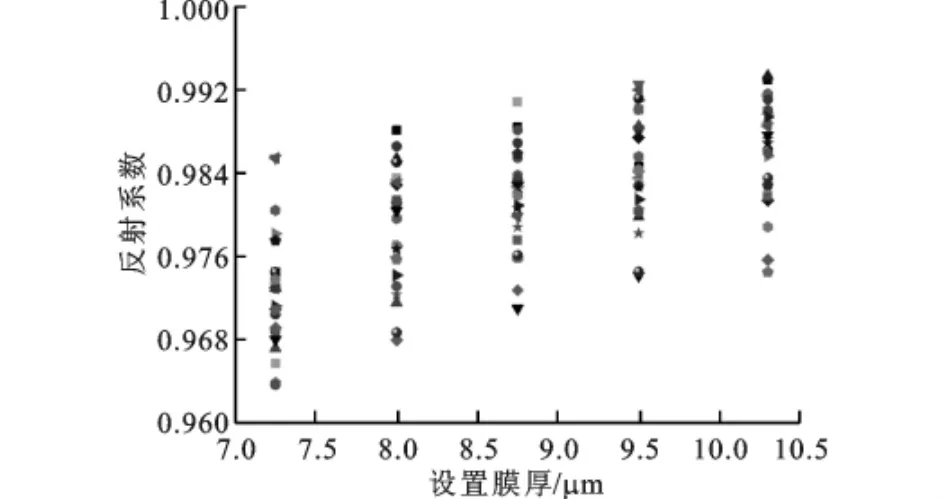
图13 由k值得到的较厚润滑膜时的反射系数值

由式（8）得到不同膜厚时回波信号的反射系数如图12、图13所示，这一结果也表示了在较厚的膜厚时分析得到的反射系数波动较大，这些波动由测量噪声与频谱分析误差带来，同时也由刚度模型法的适用范围决定。如图4所示，该方法在较厚膜厚10μm附近，反射系数值逐渐接近于1，较大的膜厚变化由很小的反射系数变化来反映，反射系数分析过程中的误差使得这一范围内的膜厚分辨力较低，但这不影响刚度模型法在微米及亚微米级润滑膜厚检测中的作用。最后，根据反射系数结果由式（2）得到实际膜厚测量结果与设置膜厚的比较如图14、图15所示，多次测量反映了该方法的正确性。测量的最小膜厚约为2.3μm，这由轴瓦表面粗糙度和润滑剂特性决定，实际检测过程中只能无限接近于膜厚值0，而不可能达到0。实验结果也说明，在较小膜厚时，该方法有较高的测量准确性，而随着膜厚增加，膜厚测量结果的波动也加大，这与反射系数波动的形成原因是相同的，而设置膜厚达到7.25μm后，虽然单次的膜厚测量结果不能反映实际的膜厚状态，但多次测量结果的分布趋势及其均值则较好地反映了膜厚的变化及厚度值。

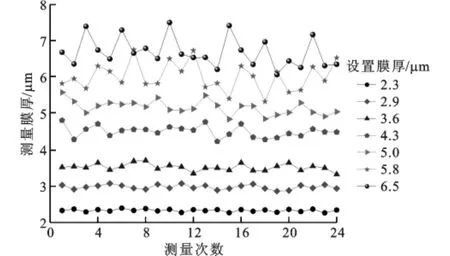
图14 润滑膜厚多次检测结果与设置膜厚比较

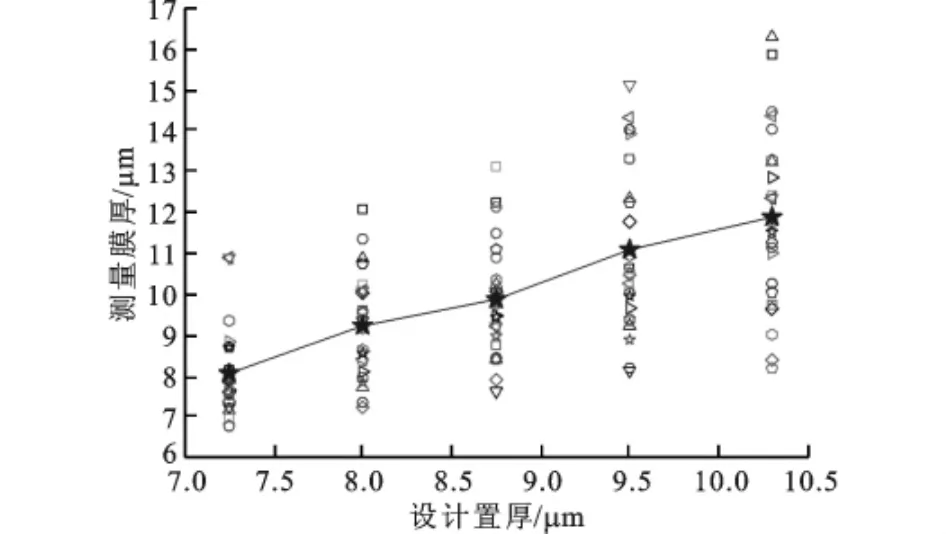
图15 较厚润滑膜时膜厚检测结果与设置膜厚比较

4 总 结

在滑动轴承润滑膜厚度的超声波检测中，当轴瓦合金衬层厚度小于所用超声波脉冲宽度的一半时，轴承基体-衬层界面的反射回波与包含润滑膜厚信息的衬层-润滑膜界面的反射回波相叠加，无法应用基本的超声刚度模型法对这一情况时的润滑膜厚进行检测。根据叠加信号的频域分析方法，对薄衬层结构滑动轴承的润滑膜厚超声检测方法进行了理论分析。在原有需要取得轴瓦-空气界面参考反射回波信号的基础上，由厚衬层轴瓦试件或理论计算得到基体-衬层界面的回波信号幅值谱。然后分别取得参考回波、不同膜厚回波时叠加信号与基体-衬层界面回波的频域幅值比，并按叠加信号间幅值比关系得到包含膜厚信息回波成分与基体-衬层界面回波成分在峰值频率处的幅值比，由此幅值比的变化关系得到膜厚测量过程中的反射系数值并最终确定润滑膜厚度值。设计了高精度膜厚标定测试实验台，对薄衬层结构轴瓦润滑膜厚度进行了检测实验，实验结果验证了这一方法的正确性。

［1］ DWYER-JOYCE R S，DRINKWATER B W，DONOHOE C J.The measurement of lubricant-film thickness using ultrasound［J］.Proceedings of the Royal Society of London：Series A Mathematical Physical and Engineering Sciences，2003，459（2032）：957-976.

［2］ HARPER P，HOLLINGSWORTH B，DWYER-JOYCE R S，et al.Journal bearing oil film measurement using ultrasonic reflection ［C］∥ Proceedings of the 29th Leeds-Lyon Symposium on Tribology.Amsterdam，Netherlands：Elsevier Science BV，2003：469-476.

［3］ DWYER-JOYCE R S，HARPER P，DRINKWATER B W.A method for the measurement of hydrodynamic oil films using ultrasonic reflection ［J］.Tribology Letters，2004，17（2）：337-348.

［4］ REDDYHOFF T，KASOLANG S，DWYER-JOYCE R S，et al.The phase shift of an ultrasonic pulse at an oil layer and determination of film thickness ［J］.Proceedings of the Institution of Mechanical Engineers：Part J Journal of Engineering Tribology，2005，219（6）：387-400.

［5］ DRINKWATER B W，ZHANG J，KIRK K，et al.Ultrasonic measurement of rolling element bearing lubrication using piezoelectric thin film transducers［C］∥Proceedings of the AIP Conference.New York，USA：AIP Publishings，2008：888-895.

［6］ ZHANG J，DRINKWATER B W.Thin oil-film thickness distribution measurement using ultrasonic arrays［J］.NDT ＆ E International，2008，41（8）：596-601.

［7］ SIMPSON J R W A.Time-frequency-domain formulation of ultrasonic frequency analysis ［J］.Journal of the Acoustical Society of America，1974，56（6）：1776-1781.