数据预处理对最小二乘支持向量机预报钟差的影响

雷 雨，赵丹宁

(1.中国科学院 国家授时中心，西安 710600；2.中国科学院 时间频率基准重点实验室，西安 710600；3.中国科学院 精密导航定位与定时技术重点实验室，西安 710600；4.中国科学院大学，北京 100049)

1 引言

卫星钟差(satellite clock bias， SCB)的预报在卫星导航定位系统中具有重要作用。由于星载原子钟受外界及其自身因素的影响，很难掌握其复杂细致的变化规律。因此建立精确的原子钟运行模型非常困难，相应地准确预报钟差也非常困难。目前，应用较多的卫星钟差预报方法主要有GM(1，1)模型法[1]、二次多项式模型法(quadratic polynomial， QP)[2]、ARIMA模型法[3]等。同时，伴随着机器学习理论的发展，一些非线性模型如人工神经网络(artificial neural network， ANN)[4-5]、最小二乘支持向量机(least squares support vector machines， LSSVM)[6]已被成功应用于卫星钟差预报中。然而，当采用ANN模型来进行预报时，存在易陷入局部极小、网络结构难以确定等缺点[5]，而且它是基于经验风险最小化的原则，易导致过学习现象的产生；除此之外，ANN模型是建立在大样本基础之上，如果样本量较小，则建模效果就不是很理想。而LSSVM较好地解决了小样本和局部极小等实际问题，被认为是ANN的替代方法[7]。笔者将LSSVM应用于卫星钟差的短期预报中，研究结果表明，LSSVM通过对样本的学习可以准确地预报钟差序列，非常适合于解决非线性、非平稳卫星钟差序列的预报问题[6]。本文在上述研究的基础上，结合实例详细探讨在建模时，样本数据预处理方法的选用对LSSVM钟差预报模型性能的影响。

2 LSSVM钟差预报算法及样本数据预处理方法

2.1 LSSVM钟差预报算法

由于当前时刻的钟差值与过去某个时间段内的钟差值密切相关，因此假设t+m时刻的钟差值x(t+m)可由t、t+1、…、t+m-1时刻的历史钟差值x(t)、x(t+1)、…、x(t+m-1)来进行预报，则可建立映射f：Rm→R，预报模型可表示为

x(t+m)=f[x(t),x(t+1),…,x(t+m-1)]
t=1,2,…,n-m

(1)

本文采用LSSVM来完成对非线性映射f(·)的逼近，相应的LSSVM算法见文献[8]。式(1)中，m表示嵌入维数，n为已知钟差数据个数。

表1 输入向量和输出向量的结构

由于选取不同的核函数可以构造不同的学习机，所以利用LSSVM解决具体问题时，最关键的是针对具体对象的特点选取合适的核函数，但是对于核函数的确定目前还没有明确的理论依据可以遵循[9]，只能凭经验确定。常用的核函数有径向基(radial basis function， RBF)核、线性核和多项式核，其表达式分别为

RBF函数

K(xi,xj)=exp(-xi-xj2/2σ2)

(2)

式中，σ为核宽度。

线性函数

K(xi,xj)=xixj

(3)

多项式函数

K(xi,xj)=(1+xixj)d

(4)

式中，d为多项式阶次，d=1,2,…。

在选取上述某一种函数为核函数的条件下，影响LSSVM钟差预报精度的核心参数包括正则化参数、核参数与嵌入维数。本文以交叉验证误差为评价准则，利用网格搜索算法[10]搜索LSSVM预报模型的最优参数组合。

2.2 样本数据预处理的必要性

在进行卫星钟差建模预报时，一般将可用样本分为训练样本集和测试样本集两部分。训练集的功能是对模型进行训练，训练好的模型对训练集的符合程度称为模型的学习能力，又称可塑性，而测试集的功能是对模型的泛化能力进行检验。一个性能好的模型应同时具有很好的可塑性和泛化能力。

样本数据预处理是指通过变换处理将LSSVM的输入、输出数据限制在一定范围内。在利用LSSVM模型进行卫星钟差预报时，对数据进行预处理的原因是：1)钟差序列有效位数太多，并且相邻历元钟差数值变化不大，造成LSSVM难以较好地拟合钟差模型；2)数据有效位数多引起LSSVM收敛速度慢。

2.3 数据预处理方法

假设{x(t),t=1,2,…,n}为需要进行数据预处理的样本数据，根据预处理后数值分布范围，可将预处理方法分为3种：

1)归一化

归一化的变换式为

(5)

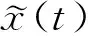
2)标准化

标准化的变换式为

(6)

3)一次差

钟差序列相邻历元间一次差的变换式为

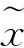
(7)

通常得到的卫星钟差相邻历元的数值变化不大，钟差相邻历元间作一次差后的差值序列有效位数减少，以全球定位系统(global positioning system， GPS)卫星钟为例，其钟差一次差序列一般在[-2，2]范围内变化。

需要说明的是，数据预处理的对象既包括训练集的输入、输出样本，也包括测试集的输入样本。与使用原始数据序列进行建模不同，这里首先对原始数据进行预处理，然后使用预处理后的数据序列进行建模，最后还原得到最终预报结果。

3 实验结果分析

3.1 实验数据选取

实验数据来自全球卫星导航系统国际服务协会(international global navigation satellite system service，IGS)网站提供的 5min间隔的事后精密GPS卫星钟差数据。以2012-07-11-08-10共31 d的数据为例，同时考虑此时的星载原子钟包括Block ⅡA Cs钟、ⅡA Rb钟、ⅡR Rb钟和ⅡR-M Rb钟4类，随机选取每类钟的卫星进行实验，本文选取的是PRN04(ⅡA Rb)、PRN08(ⅡA Cs)、PRN23(ⅡR Rb)和PRN29(ⅡR-M Rb)这4颗卫星。其中，PRN04和PRN29卫星钟差呈递增变化，PRN23卫星钟差呈递减变化，而PRN08卫星既不呈递增也不呈递减变化。

3.2 实验结果1

使用7月11日1 d(288个历元)的钟差数据进行建模，预报接下来1 d的钟差，即将7月11日及12日的数据分别作为训练样本集和测试样本集。分别使用原始数据、归一化数据、标准化数据和一次差数据序列建立LSSVM模型，并对比不同核函数对预报精度的影响。表2给出了模型使用不同数据序列、不同核函数时预报精度统计，其中，以IGS相应的精密钟差值为基准，使用均方根(root mean square，RMS)作为统计量。

从表2中可以看出：

1)不同核函数对LSSVM模型性能有重要影响。使用原始数据和归一化数据序列建模时，基于线性核函数的预报效果最好，使用差分数据序列建模时，基于RBF核函数的预报精度最高，而使用标准化数据序列建模时，基于线性和多项式两种核函数的预报效果相当，整体而言，多项式核函数稍好；

2)与不对样本进行数据预处理相比，数据预处理方法没有提高LSSVM的可塑性，不同的数据预处理方法对LSSVM的可塑性影响也是相当的；但数据预处理方法对泛化性能的改善是显著的，并且不同的数据预处理方法对泛化性的影响有很大差别，这一点可以从模型测试集的均方根误差看出。

3)LSSVM模型采用一次差数据预处理方法时预报精度最高，而运用归一化和标准化两种方法时预报精度无明显差别。

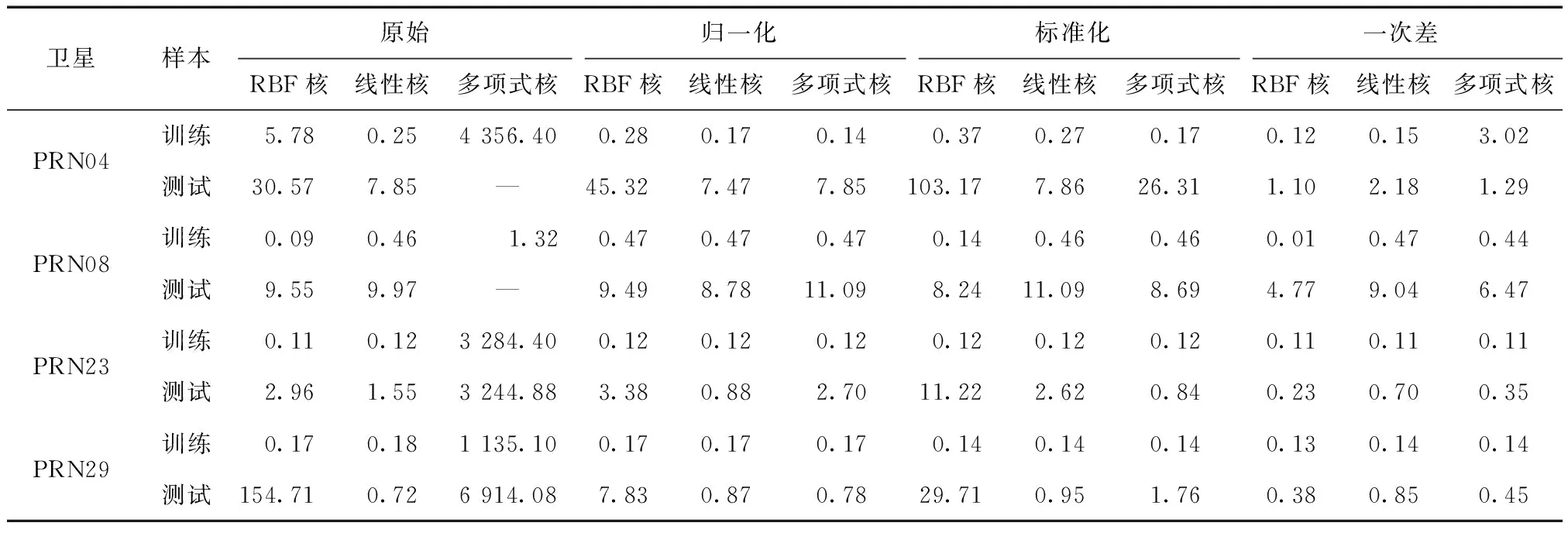
表2 基于不同数据序列、不同核函数的预报精度统计表/ns

注：“—”表示无穷大

3.3 实验结果2

为了进一步对比不同数据预处理方法的钟差预报效果，同样使用7月11日的数据进行建模，分别预报接下来7 d、14 d和30 d的钟差。为了验证LSSVM在卫星钟差预报时的优越性，将其与传统的QP模型和GM(1，1)模型进行对比分析，其中，采用11日的原始钟差数据建立QP模型，使用11日最后1 h(12个历元)的原始数据建立GM(1，1)模型。

根据3.2节的分析可知，运用不同数据序列建模时，不同核函数的适用性不尽相同。对于原始数据和归一化数据序列，这里使用线性核，差分序列使用RBF核；由于采用标准化数据序列建模时，线性核和多项式核的适用性大体相同，但线性核不需要确定核参数，可以简化计算，所以这里仍使用线性核。

表3给出了4颗卫星在LSSVM模型使用数据预处理方法前后的预报结果统计值，表3中，使用RMS和极差(Range，最大误差与最小误差之差的绝对值)作为统计量，比较分析模型使用不同数据序列时的预报效果。

从表3可以看出，LSSVM模型使用数据预处理方法时预报精度和稳定性较不使用时有了明显的提高，其中一次差数据预处理方法对预报效果的改善最为显著，归一化和标准化方法次之，并且这两种方法的改善效果相当。在实验过程中发现，使用经过数据预处理的数据序列进行建模，LSSVM的训练时间明显缩短，以利用一次差分数据作为训练数据为例，其训练时间和预报时间(7 d)之和一般在10 min以内，保证了算法的实时性，而利用原始钟差数据建模预报，需消耗时间至少20 min。

表3 预报结果统计表

下面对LSSVM模型使用各数据预处理方法时表现出的特点进行分析说明。由于使用的是IGS提供的精密钟差数据，其钟差序列自身误差很小，其精度最高可达75 ps，因此可以认为钟差预报误差是由LSSVM的建模误差所造成的。归一化和标准化方法纯粹是两种数字变换方法，只是将钟差序列限制在一定的范围内，而没有考虑到钟差序列自身表现出的特性，虽然可以明显提高LSSVM的建模精度，但不及一次差方法，这两种方法的区别也只是变换后数值分布范围不同，所以对LSSVM的建模影响程度也相当。而一次差数据预处理方法顾及了星载原子钟钟差的特点，通过相邻历元间一次差的建模方法，LSSVM模型可以较好地拟合钟差模型，进而可以提高LSSVM模型的预报精度和泛化能力。但一次差方法本身也存在一定的缺点，即经过数据的一次差处理和预报后的钟差还原，根据误差传播定律可知，这样会使预报结果所含的误差变大。然后从实验结果可以看到，即使对于30 d的长期预报，使用一次差方法时LSSVM的钟差预报效果仍比不使用时得到了明显提高，这是因为由原钟差序列有效位数太多引起的LSSVM模型难以较好地拟合钟差模型所造成的误差远大于由相邻历元作差对建模所造成的预报误差。值得一提的是，如果LSSVM建模时，所使用的钟差数据含有一定的系统误差，则基于一次差方法的LSSVM模型会得到更好的预报效果。

为了验证基于LSSVM的钟差预报性能，将基于一次差方法的LSSVM模型同QP模型和GM(1，1)模型加以比较，表2给出了4颗卫星的QP模型、GM(1，1)模型和LSSVM模型的预报均方根误差和极差，限于篇幅，仅给出了PRN04卫星7 d、14 d和30 d的误差比对图，见图1～图3。

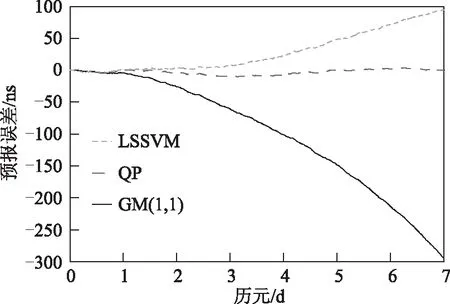
图1 PRN04卫星预报7 d误差

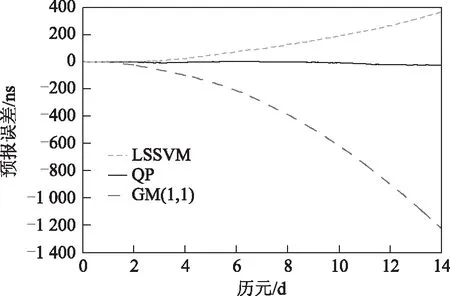
图2 PRN04卫星预报14 d误差

图3 PRN04卫星预报30 d误差

结合图1～图3和表3可以看出，与QP模型和GM(1，1)模型相比较而言，基于一次差方法的LSSVM模型对7 d、14 d和30 d的预报精度均有显著改进，尤其对于变化比较复杂、严重老化的Block ⅡA Cs钟和ⅡA Rb钟，基于LSSVM模型的预报效果仍比较理想，这说明LSSVM在处理非线性钟差的预报问题时具有一定的优势。

4 结束语

以样本数据预处理对基于LSSVM的卫星钟差预报的影响为切入点，探讨了不同数据预处理方法对钟差预报结果的影响。对预报结果进行分析，得到以下结论：

1)使用LSSVM进行卫星钟差预报，数据有效位数的多少对LSSVM的预报性能有重要影响，因此在使用LSSVM前对有效位数多的原钟差数据序列进行适当的处理可以提高LSSVM的预报性能；

2)使用预处理后的数据序列进行建模时，各种核函数的适用性不尽相同，需要根据实际情况来选择合适的核函数；

3)归一化、标准化和相邻历元间一次差的3种数据预处理方法，在保证模型可塑性的情况下，对模型的泛化能力都有显著改进，其中基于一次差方法的改进效果最为明显，归一化和标准化方法次之，并且这两种方法对泛化能力的改善程度相当；

4)基于一次差方法的LSSVM模型预报性能明显优于传统的二次多项式模型和灰色系统模型，可以考虑作为一种较为有效的导航卫星钟差短期、中长期预报方法使用。

[1] 崔先强，焦文海.灰色系统模型在卫星钟差预报中的应用[J].武汉大学学报：信息科学版，2005，30(5)：447-450.

[2] 郑作亚，卢秀山.几种GPS卫星钟差预报方法比较及精度分析[J].山东科技大学：自然科学版，2008，27(4)：6-11，15.

[3] 徐君毅，曾安敏.ARIMA(0，2，q)模型在卫星钟差预报中的应用[J].大地测量与地球动力学，2009，29(5)：116-120.

[4] 郭承军，滕云龙.基于小波分析和神经网络的卫星钟差预报性能分析[J].天文学报，2010，51(4)：395-403.

[5] LI Xiao-yu，DONG Xu-rong，ZHENG Kun，et al.Research of Satellite Clock Error Prediction Based on RBF Neural Network and ARMA Model[EB/OL].[2013-08-12].http：//link.springer.com/chapter/10.1007%2F978-3-642-37407-4_29#page-1.

[6] 雷雨，赵丹宁.基于最小二乘支持向量机的钟差预报[J].大地测量与地球动力学，2013，33(2)：91-95.

[7] VAPNIK V N.An Overview of Statistical Learning Theory[J].IEEE Transactions on Neural Networks，1999，10(5)：988-999.

[8] SUYKENS J A K，VANDEWALLE J.Least Squares Support Vector Machine Classifiers[J].Neural Processing Letters，1999，19(3)：293-300.

[9] 祝志慧，孙云莲，季宇.基于EMD和SVM的短期负荷预测[J].高电压技术，2007，33(5)：118-122.

[10] 王兴玲，李占斌.基于网格搜索的支持向量机核函数参数的确定[J].中国海洋大学学报，2005，35(5)：859-862.