双曲螺线曲率中心轨迹在一点邻近的结构

崔凤午

(白城师范学院 数学系，吉林 白城 137000)

1 双曲螺线曲率中心的曲率和挠率

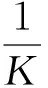
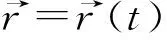
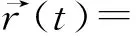
结论1设双曲螺线的曲率为k(t)，挠率为τ(t)，则

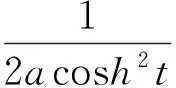
结论2双曲螺线的曲率中心的方程为

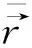
证明设曲线的曲率中心轨迹方程

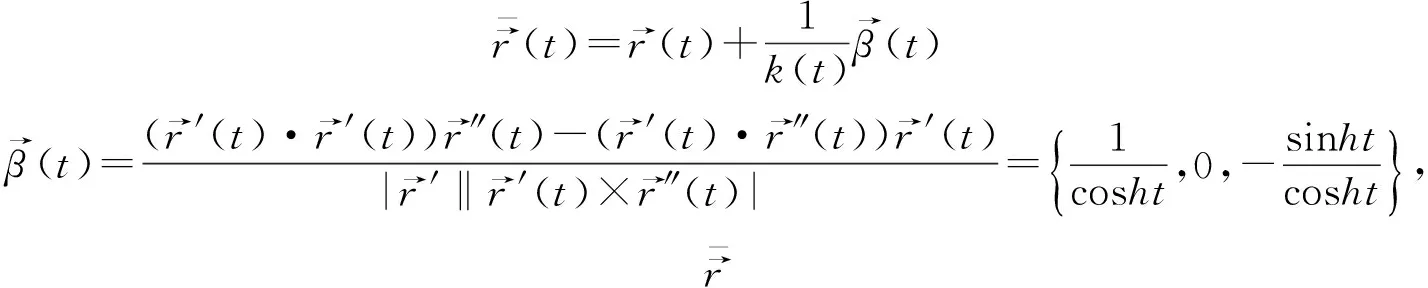
={3acosht,asinht,at-2asinhtcosht}．

定理1双曲螺线的曲率中心轨迹的曲率为

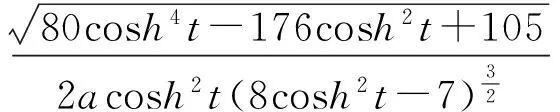
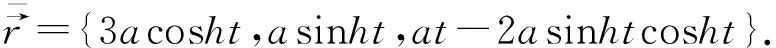
由曲率公式得

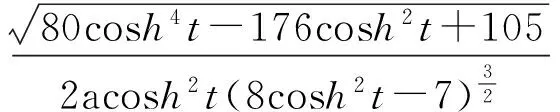
定理2双曲螺线的曲率中心轨迹的挠率为

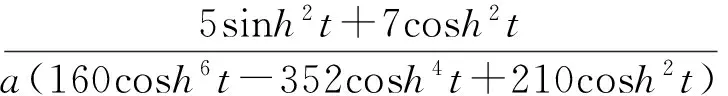
证明由定理1证明可得

由挠率公式

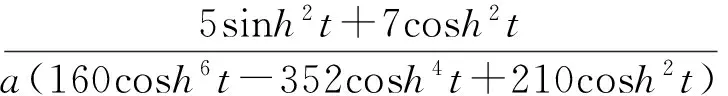
结论4双曲螺线的曲率中心轨迹的挠率大于零

证明由定理2知

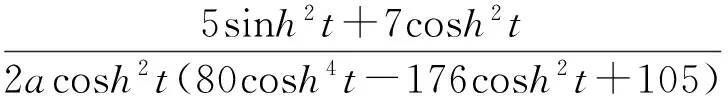
将80cosh4t-176cosh2t+105看成以cosh2t为变量的二元一次函数

a=80>0，=b2-4ac=1762-4×80×105<0

所以

80cosh4t-176cosh2t+105>0

即双曲螺线的曲率中心的挠率大于零．

2 双曲螺线曲率中心在一点邻近的结构[3-5,10]

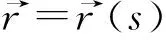
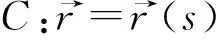
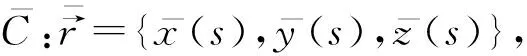
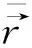
引理3曲线在一点邻近和它的近似曲线有相同的曲率和挠率

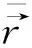
下面我们通过双曲螺线曲率中心轨迹的近似曲线在基本三棱形的三个平面上的投影来观察双曲螺线在一点邻近的形状．

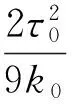
它是半立方抛物线．

在从切平面上的投影是

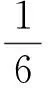
它是立方抛物线．

在密切平面上的投影是

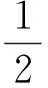
它是抛物线．

通过以上三个投影的立体图形可以看出空间曲线在一点邻近的近似形状．因为双曲螺线曲率中心的挠率[8]

所以曲线上的点有以下变化规律

-∞0sx*y*z*--+-++++

综上得以下结论

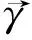
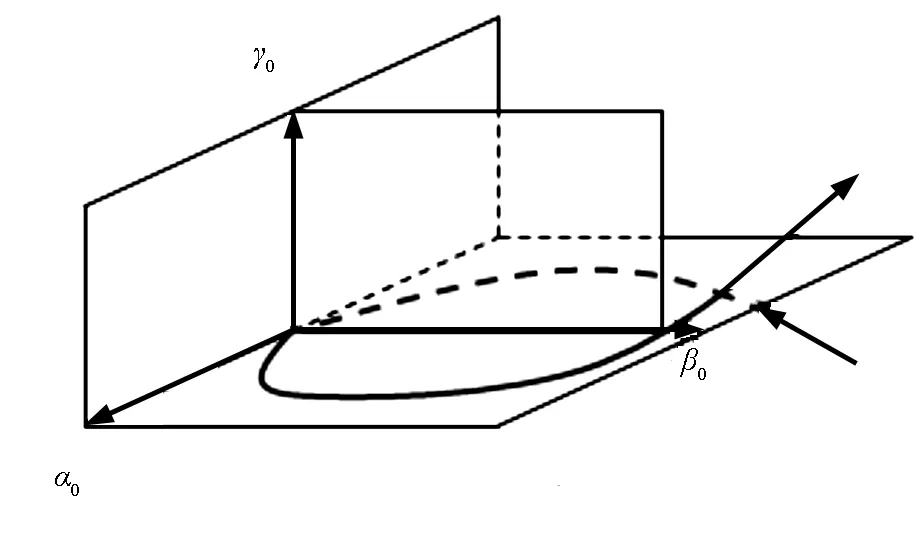
图1 曲线由下往上成右旋曲线

定理1、定理2给出双曲螺线曲率中心轨迹的曲率、挠率计算公式，揭示了双曲螺线曲率中心弯曲和扭曲规律，定理3讨论了双曲螺线曲率中心在一点邻近的结构．

[1]梅向明，黄敬之.微分几何(第4版)[M].北京:高等教育出版社,2008.

[2]崔凤午.空间曲线曲率中心轨迹的曲率与挠率[J].武汉科技学院学报 2010(2):41～43.

[3]傅朝金.空间曲线的曲率和挠率[J].高等函授学报(自然科学版),2003(5):13～14

[4]陈省身,陈维桓.微分几何讲义[M].北京:北京大学出版社,2001.

[5]吕林根,徐子道.解析几何(第3版)[M].北京:高等教育出版社,2008.

[6]梅向明,王汇淳.微分几何(第4版)[M].北京:高等教育出版社,2004.

[7]崔凤午. 一般螺线曲率中心轨迹的曲率与挠率[J]. 白城师范学院学报,2009,(6):1～4.

[8]崔凤午. 泛函微分方程在研究二次曲线性质中的应用[J]. 吉林师范大学学报(自然科学版)，2004，(3)：31～33.

[9]崔凤午. 双曲螺线曲率中心轨迹的曲率与挠率[J]. 南阳理工学院学报 2011,(3):114～116.

[10]崔凤午.维维安妮(Viviani)曲线在一点邻近的结构 [J]. 白城师范学院学报,2011,(3):1～5.

[11] 崔凤午. Viviani曲线的曲率、挠率及Frenet公式[J]. 吉林师范大学学报(自然科学版),2011,(3):28～29.