高频驱动超磁致伸缩致动器的磁场设计与分析

2014-01-15张志富陈定方李涛涛邓思琪

湖北工业大学学报 2014年4期

张志富，陈定方，李涛涛，邓思琪

（武汉理工大学智能制造与控制研究所，湖北武汉430063）

超磁致伸缩材料（GMM）主要是指以（Tb，Dy）Fe2化合物为基体的合金。作为高效智能材料的典型代表之一，超磁致伸缩材料有着输出位移大、抗载能力强、磁机转换效率高以及响应速度快等性能优势［1］，但是国内对超磁致伸缩致动器（GMA）的研究仍然存在以下几个方面问题：一是较多地集中在准静态或者低频域的范围内，对高频域内的研究较为薄弱；二是设计过程中，对于超磁致伸缩致动器的磁场多以轴线方向上磁场强度为检验和设计标准，不利于建立精确的三维空间磁场数值计算模型。针对上述问题，本文设计出一款用于高频的超磁致伸缩致动器，在ANSYS平台上建立了精确的励磁线圈空间磁场模型［3］，对磁场均匀性［3－4］，以及交流驱动磁场与静态偏置磁场进行了仿真与分析。

1 高频驱动的超磁致伸缩致动器设计

高频域下的GMA与工作于静态（准静态）的GMA存在异同。本文参考传统静态超磁致伸缩致动器的设计方法，同时考虑了交流电驱动引起的非线性因素，设计出高频驱动下小物理体积、大能量输出的超磁致伸缩致动器。所设计的超磁致伸缩致动器如图1所示。

在合适的偏置磁场下，可使GMM棒工作于伸缩性能良好的线性区域。此时，当输入为交变磁场时，超磁致伸缩棒将会产生与交变磁场同频率的交变输出位移，使得GMM棒体发生位移振动的运动。图2为偏置磁场下正弦信号、方波信号驱动磁场时GMM的振动输出原理图。

与传统的压电材料相比，超磁致伸缩材料具有优良的磁弹性能，其反应速度快，响应时间极短，可达6～10s，而且其能量密度高达14～25J／m3。为此，在高频率的驱动磁场下，将会产生极快的响应与极高的振动能量输出，充分发挥出超磁致伸缩材料优良的材料性能。

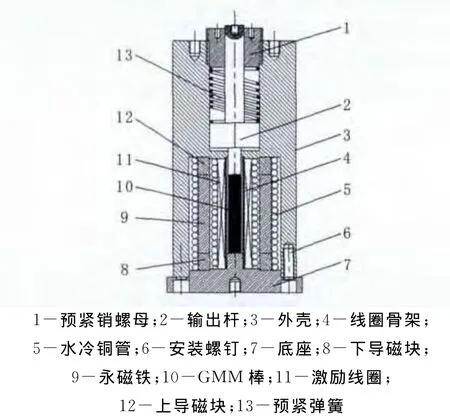
图1 高频超磁致伸缩致动器总体结构图

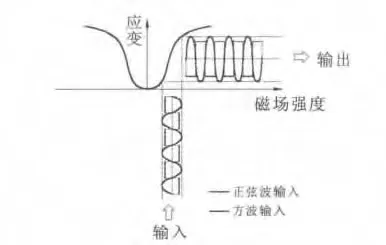
图2 超磁致伸缩材料振动机理图

2 高频GMA动态磁场有限元分析

2.1 静态驱动磁场分析

通过对激励线圈磁场模型的分析，掌握了螺线管内部磁场分布特性，为驱动线圈设计尺寸的选择与优化提供了理论基础。而在具体器件应用中，磁场的分布情况还与器件结构尺寸、漏磁情况及材料的磁导率有着密切关系，在超磁致伸缩致动器的磁场设计中，需要对这些因素进行综合考虑。如果采用理论磁场计算方案对GMM棒内部磁场进行计算，则必须要面对理论磁场数学建模难度过大的难题，可操作性不强［5］。为此，采用基于“场”的有限元方法完成对超磁致伸缩致动器磁场的整体设计与分析。GMA的闭合磁路主要由底座、下导磁块、GMM棒、上导磁块、输出轴及壳体组成，各个部分电磁学参数见表1。

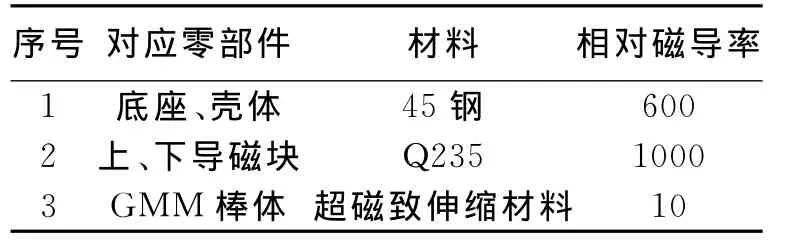
表1 GMA闭合磁路零件材料电磁学参数表

虽然GMM棒体为叠片式结构，但在静态电流驱动时不存在涡流影响，可视GMM棒为轴对称结构，忽略少量的不对称结构影响，GMA可以看作完全轴对称结构，在建模过程中采用轴对称建模方法，只需建立其轴对称截面即可模拟整个GMA的模型，使计算量大大降低。对所建立的模型进行网格划分、加载与求解，最终的分析模型与结果见图3。

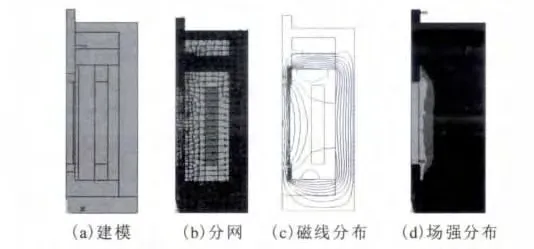
图3 超磁致伸缩致动器静态磁场仿真图

从分析结果可见，驱动线圈所产生的大部分磁力线通过GMM棒，经过上导磁块、输出轴、外壁底座与下导磁块形成闭合回路。虽然输出轴与外壁之间存在少量间隙，但由于空气磁导率较小，漏磁极少。从磁场强度分布来看，分布在GMM棒上的磁场强度较大，磁能较多地用于对GMM棒的驱动，说明所设计的GMA磁路合理。

2.2 交流驱动磁场设计有限元分析与激励频率讨论

在交流驱动磁场下，电阻率将会在GMM棒中产生涡流，而涡流将会对GMM棒产生涡流热效应与集肤效应影响，涡流热效应通过温度变化影响超磁致伸缩材料的各项性能，集肤效应则会引起超磁致材料内部磁场非线性问题。图4给出了不同驱动频率的电流下GMA磁场强度分布状况，图5给出GMM棒中间截面磁场强度随径向距离的变化。

图4 不同驱动频率下GMA磁场分布图

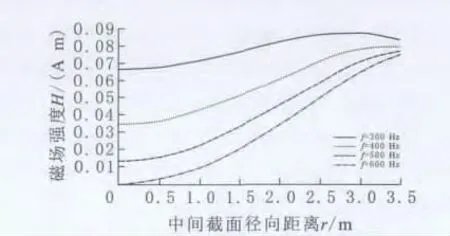
图5 GMM棒磁场强度随径向距离变化图

从结果可以看出，在交流电驱动下，GMM棒中磁场分布具有如下特点：1）在交流电流驱动下，沿着GMM棒体径向方向上，呈现出靠近轴线方向上磁场强度小，远离轴线处的磁场强度大的特点；2）随着驱动频率逐渐增大，分布在GMM棒体上的磁场强度整体逐渐减小。在越靠近轴线处，磁场强度降低幅度更大，当驱动频率达到600Hz时，轴线处磁场强度减小到零，而远离轴线靠近棒体外径处，磁场强度变化量很小。

GMM棒体内磁场分布特点，证明了交流驱动时磁场分布集肤效应导致GMM棒中各部分伸长不均匀，使得GMM棒外表伸长量大于内部伸长量，进而引起GMM棒芯部出现应力集中现象，从而影响GMM使用寿命与材料性能。为了充分发挥超磁致伸缩材料的性能优势，将GMM棒体沿轴向切割为多层叠片，使用绝缘的环氧树脂对各叠片进行粘贴，达到抑制涡流效应的作用。

3 偏置磁场设计及优化

在实现偏置磁场的仿真过程中，采用圆筒永磁铁、圆柱永磁铁及偏置线圈组合作用或单个作用的多种不同设计方案。GMA结构优劣评判及最优偏置磁场设计方案见表2。

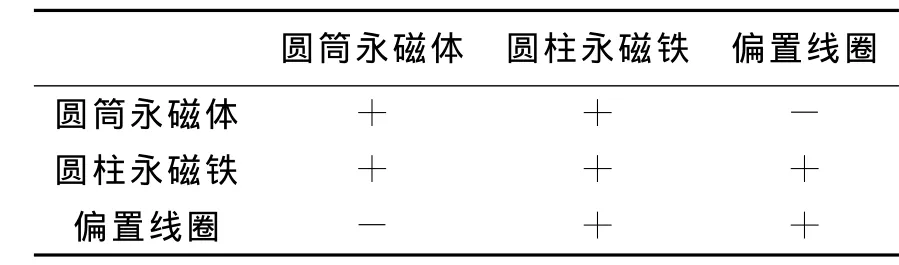
表2 偏置磁场设计方案组合表

由表2可知，设计方案的组合情况呈现以对角线为轴的对称现象，为了避免重复设计，只需完成对角线及其以下（上）设计方案的仿真即可。各设计方案的偏置磁场的磁力线分布、磁场强度云图及GMM棒体上磁场强度如图6所示。可以看出，单独圆筒永磁体与单独线圈的两种设计方案所产生的偏置磁场均匀度较好。考虑到偏置磁场所需磁场强度较大，采用偏置线圈的设计方案线圈发热情况严重，为此采用单独圆筒永磁体作为偏置磁场的设计方案。