高性能混凝土徐变系数的计算和分析
2014-01-15李威,苏骏
李 威,苏 骏
(湖北工业大学土木工程与建筑学院,湖北 武汉430068)
随着混凝土材料在桥梁、地下工程、海洋和近海、各种民用建筑等建筑结构中应用日渐增多,其徐变问题亦变得愈来愈突出。徐变是混凝土在持续荷载作用下的固有属性,是一个随时间逐渐变化的阶段,徐变的最终结果将造成混凝土结构中内力与变形的改变,混凝土结构的徐变分析与计算是土木工程界长时间研究和探索的重点。徐变对混凝土结构的内力重新分布和几何变形有着重要影响,并且直接影响结构的耐久性。因为影响混凝土徐变特性的因素众多,迄今为止尚未有一种可以完整解释混凝土徐变特性的理论。本文在对国内外不同的混凝土徐变计算模型进行总结的基础上,通过模型的理论计算值与试验值进行比较分析,为工程结构的设计和施工提供理论参考。
1 线性徐变的假设
由于目前非线性徐变理论尚不成熟,人们通常假设徐变同应力变形存在线性关系,以此来求解混凝土徐变。同时,在遵从Boltzman叠加原理前提下,连续的应力形成的总应变
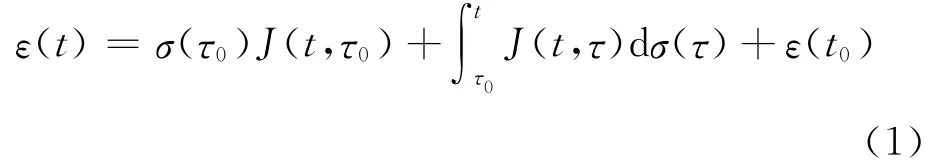
其中:τ0表示为初始加载龄期;σ(τ0)为初始加载应力;J(t,τ0)为柔度函数;ε(t0)为τ0时刻载入t时刻的徐变应变。
在以下适用范围内,实验结果与叠加原理的预测结果有较好的吻合:工作应力小于等于0.5σ时,应变值将不在该阶段减小;徐变过程中,试件的干燥程度不太明显;初始加载以后,应力值增幅不大。
2 混凝土徐变预测模型
徐变对结构的应力分布产生重要的影响。许多科研学者和机构在大量的试验基础上,提出了不同的徐变模型,如:CEB-FIP系列模型、ACI-209系列模型、B-P系列模型和GL2000模型等。因为影响混凝土徐变的因素较多,实验室的特定条件和研究重点不同,各预测模型在研究问题时各有取舍,以这些模型作为实际工程应用的依据能否达到预期的效果,尚须进一步的实践检验。
2.1 CEB-FIP系列模型
CEB-FIP系列模型是由国际预应力混凝土协会(FIP)和欧洲混凝土委员会(CEB)创立的,先后提出了三个模型:70模型、78模型、和90模型[1]。78模型的徐变系数采用将弹性变形和塑性变形相叠加的方式表现,并将塑性变形分为延迟塑性流变与初始急变。90模型较多考虑了初始阶段就可获取的参数,如:抗压强度、构件尺寸、加载龄期、平均相对湿度等,使用双曲幂函数形式表示了徐变系数随着时间改变的规律,表达式为
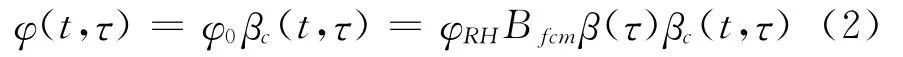
式中:φ0为名义徐变系数;φRH为相对湿度修正系数;βfcm为混凝土强度的修正系数;β(τ)为加荷龄期修正系数;βc(t,τ)徐变进程时间系数。90模型不再使用78模式的累加结构形式,用名义徐变系数表示各参数变化与徐变系数的关系,并对其随时间改变的结果不断修正,采用连乘结构形式模型,避免了直接线性叠加带来的误差。90和78模型分别被我国新老桥规采用,对我国混凝土结构设计有较大影响。
2.2 ACI-209系列模型
ACI-209系列模型由美国混凝土协会(ACI)推荐,先后有78模式、82模式、92模式[2]。82模式细致的考虑了混凝土的配合比,并用双曲线函数的时间系数,但未考虑混凝土强度的影响,收缩和徐变效应与实验情况吻合较差[3]。92模式在82模式上进行了改进,不仅考虑了混凝土的各种影响因素,同时没有区分弹性变形和塑性变形,明确采用干燥开始的持续时间取代之前的计算龄期。其徐变系数表达式为
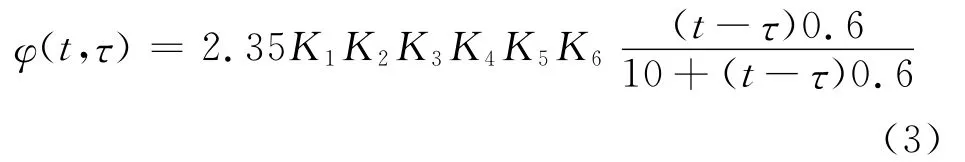
式中:K1~K6依次为混凝土加载龄期、环境相对湿度、混凝土构件平均厚度、混凝土稠度、细骨料含量、空气含量影响系数。92模型首先依据的工作环境来确定各项参数,再通过时间因子修正徐变结果。该模型能够预测非标准状态下混凝土的徐变,如:不同环境相对湿度、尺寸因子及不同混凝土构成。
2.3 B-P系列模型
B-P系列模型由美国Bazant教授在1979年逐渐建立,分别有B-P模型、BP2模型和1995年提出的B3模型[4]。B3模型以固化理论为建立依据[5],结合流变理论、弹性理论和粘弹性理论,该理论假设徐变的时间进程中力学性质和弹性相体积不变而混凝土材料的粘性相和粘弹性相体积不断增多。其表达式为
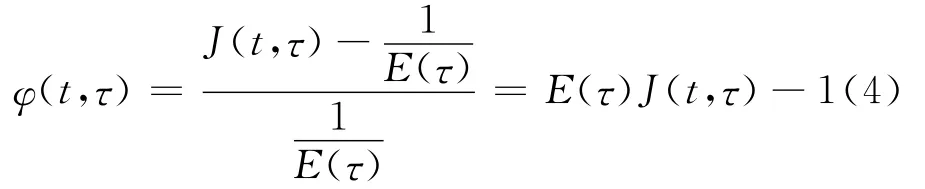
B3模型定义的徐变由基本徐变和干燥徐变构成,并直接通过混凝土材料组成和特性中得出徐变结果。材料参数和时间函数的组合表达了该模型的徐变预测公式,可以简易的以材料的短时间试验来确定混凝土的某一参数,具备较强的可行性和可靠性。从目前的对比试验来看,B3模型的预测结果最好。
2.4 GL2000模型
美国Gardner和Zhao的理论中指出,徐变系数的概念被广泛应用于包括ACI209(1982)以及CEBFIP(1990)的多数徐变预测模型中,Ross型双曲线函数也被普遍用来描述时间效应。然而不断的研究表明,时间的增加并不能使徐变值而达到极值。对此,两人基于大量的长期徐变数据分析后,提出了G-Z修正模型。该模型考虑多种影响混凝土徐变的因素,并给出了早期混凝土强度计算方法。1999年的ACI209委员会提出了混凝土收缩徐变预测模型的几项要求,在以上准则基础上,G-Z模型由Gardner和Lockman修改,提出了GL2000模型[6]。在该模型中,骨料的刚度由抗压强度以及弹性模量的测量值来调整确定,从而预测徐变。在收缩计算中取用28d平均强度,并简化了计算方法;徐变系数计算中只考虑多个关键因素,并对于加载前的干燥状况,单独采用一项修正系数修正,该模型参数选取适宜,计算较为简便,应用方便。
3 常用徐变模型与试验结果的比较
为了验证各种徐变模型的预测精度,本文对CEB-FIP模型、ACI模型、B-P模型和GL2000模型的徐变预测值与实验结果进行对比分析。
3.1 实验设计
本文以荆州长江公路大桥通航孔主梁C60混凝土配合比及收缩徐变试验[7]对比数据。该试验混凝土胶凝材料为华新水泥股份有限公司生产的625#普通硅酸盐水泥(编号:W1)和葛洲坝水泥厂生产的625#普通硅酸盐水泥(编号:W2);砂分别采用岳阳、洞庭湖的天然砂,碎石产地为宜昌;外加剂分别采用UNF-1和KFDN-SP8。原材料用量见表1。

表1 材料用量 kg/m3
在该试验中选取15cm×45cm的混凝土圆柱体试件尺寸,并预埋DI-25型电阻应变计观测混凝土变形。为了确保混凝土在实验期间相对湿度为100%,雾室养护48h以后,试件要用白铁皮筒进行封装,并放入(20"2)℃恒温徐变室内。试验过程参照《水工混凝土试验规程》(SD105-82)规定进行。
3.2 徐变的预测值与实际值的对比分析
根据试验实测结果及模型的计算公式,得出两种不同配合比下高性能混凝土徐变系数的计算结果(图1、图2)。
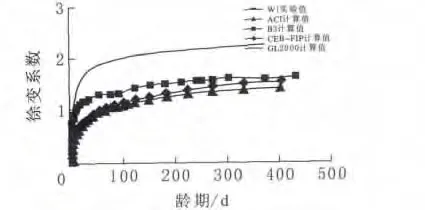
图1 W1的理论值与试验值的比较
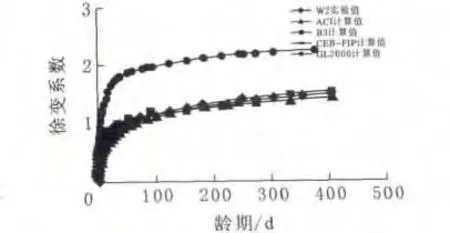
图2 W2的理论值与试验值的比较
由图1可以看出:持荷时间对混凝土最终的徐变系数影响很大,在W1配合比下,随着持荷时间逐渐增加,徐变系数逐渐增大,但单位时间的增加程度逐渐减小。在加载的初期(10d内),四种模型计算值都与试验结果较为接近,徐变逐渐增大,梯度增加(15~100d)。随着龄期的增长,水泥不断水化,混凝土的强度不断增高,徐变速率逐渐趋于平稳。
对比几种徐变模型的预测结果和实测值可以发现:GL2000模型在持荷10d后,仍然保持较高的增长速率,待水化完全以后趋于平稳,但403d的徐变计算值仍比试验值大35%左右,明显高于试验值。CEB-FIP和ACI模型的总体预测值偏低于试验情况,在加载初期两种模型的徐变预测情况基本一致,但在250d以后,CEB-FIP模型逐渐与实测值接近,ACI模型的徐变趋势仍保持不变。B3模型的预测情况与试验结果吻合良好。
分析图2的预测情况:GL2000的总体徐变趋势与W1的较为接近,其他三组模型的计算结果与试验值的重合度较高,预测精度较好。GL2000模型的预测值较大,B3模型与试验结果高度重合,CEB-FIP和ACI模型的结果稍有偏差,但仍有较高的预测精度。
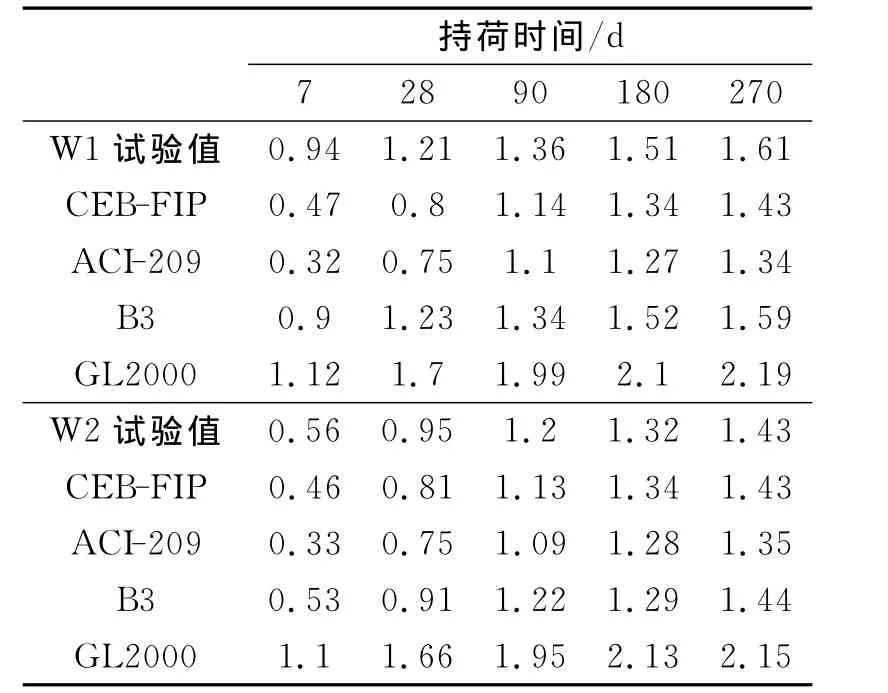
表2 徐变系数试验值与计算值的比较
表2给出了徐变系数试验结果与4种模型计算结果的对比。结果表明:不同配合比下,各模型预测情况与试验结果均有一定的差异。两种配合比下,B3模型的计算值与试验值吻合最好,误差均在3%之内;GL2000计算值高于试验值;CEB-FIP和ACI-209模型的总体预测情况较试验值偏低,但ACI-209模型在W2配合比下有更好的预测结果;CEB-FIP在 W1配合比下预测精度略低于B3模型,在W2配合比下预测情况较好。
4 结语
1)徐变模型的选取对于预测徐变的发展情况有着至关重要的作用。对比几种模型发现,GL2000模型、B3模型、CEB-FIP和ACI四种模型计算出的徐变系数依次减小,CEB-FIP和ACI模型的计算结果较为接近,GL2000模型的徐变发展速率和徐变系数值明显偏大。
2)对比试验结果表明,B3模型的计算值在两种不同配合比情况下都最接近实测值,是精度最高、最安全的模型。GL2000模型过于高估了徐变效应,CEB-FIP和ACI模型在徐变初期均低估了初期的徐变效应,但ACI模型对后期徐变效应的预测更为保守。
3)编号为W1和编号为W2的两种混凝土的徐变系数并不太大,编号W1的混凝土徐变要大于编号W2的混凝土徐变,对于预测混凝土徐变变形,采用B3模型较为合理。
[1] CEB欧洲国际混凝土委员会.1990CEB-FIP模式规范(混凝土结构)[S].中国建筑科学研究院译.北京:中国建筑工业出版社1991.
[2] 李恩良.预应力混凝土桥梁徐变计算方法对比分析[J].世界桥梁,2011(06):54-57.
[3] ACI Committee 209,ACI SP27-3.Prediction of creep,shrinkage and temperature effects in concrete structures[S].American Concrete Institute,1992:15-21.
[4] 丁文胜,吕志涛,孟少平,等.混凝土收缩徐变预测模型的分析比较[J].桥梁建设,2005(06):13-16.
[5] Creep and shrinkage prediction model for analysis and design of concrete structures-model B3[J].Materials and Structures,1995,28(06):357-65.
[6] 陈志华.混凝土徐变预测模型的对比分析[J].桥梁建设,2006(05):76-78.
[7] Gardner N J,Lockman M J.Design provisions for drying shrinkage and creep of normal-strength concrete[J].ACI Materials Journal,2001,98(02):159-167.
[8] 陈志华,彭少民,蒋沧如,等.荆州长江公路大桥主梁高性能混凝土徐变试验[J].中国公路学报,2006,19(04):98-102.
