立式锥形混合器桨叶结构的应力变形分析

2014-01-15雷经发陈雪辉林智雄

湖北工业大学学报 2014年2期

雷经发，陈雪辉，黄磊，林智雄

（安徽建筑大学机械与电气工程学院，安徽合肥230601）

混合器桨叶作为锥形混合器的重要工作部件，其性能优劣直接决定着混合器的实际工作效率高低，因此桨叶的计算和研究是设计计算的核心部分。由于目前桨叶的受力变形难以通过测试设备进行直接测量，因此，必须采用计算机仿真的方法进行相关力学特性分析。本文采用有限元方法及结构有限元分析工具研究桨叶的变形情况，在提供物料的密度和桨叶的转速基础上，估算出载荷的大小并将其转化为桨叶应力计算模型中的载荷条件，进一步分析计算可得到桨叶的应力应变和变形数据，为混合器的设计优化提供理论依据。

1 锥形混合器三维模型的建立

图1为某锥形混合器桨叶结构的二维图，考虑到本文后续分析过程中重点关注桨叶结构的受力变形情况，因此根据其具体的结构尺寸在三维软件Pro／E中仅有针对性的建立该锥形混合器桨叶结构的三维模型，如图2和图3所示。需要指出的是，为便于后续导入Hypermesh中进行网格划分，应将在Pro／E中建立的三维模型保存为通用的文件传输格式如iges、stp等［1］，本文采用文件传输过程中数据损失较小的stp格式文件。

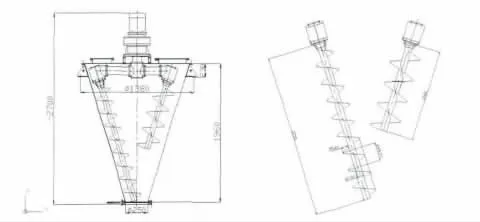
图1 某锥形混合器桨叶结构

图2 长轴桨叶的三维模型

图3 短轴桨叶的三维模型

2 网格的划分

将Pro／E导出的stp格式的模型文件导入到Hypermesh中进行网格的划分处理。通过对该模型的分析，可知锥形混合器桨叶结构的长轴桨叶和短轴桨叶均由两部分组成，一部分为圆柱轴，另一部分则为螺旋面。因此，应分别对圆柱轴和螺旋面进行网格划分，但须保证在二者网格接触部位的节点重合，以保证后续分析过程中计算的正确性。图4和图5分别为划分好网格后的长轴桨叶和短轴桨叶模型。

图4 长轴桨叶的网格模型

图5 短轴桨叶的网格模型

事实上对于锥形混合器整个工作过程而言，不论是长轴桨叶还是短轴桨叶，其整体受力情况较为类似。因此，为了简化分析计算和了解混合器桨叶的受力变形情况，在实际分析过程中从该混合器桨叶上截取一段进行分析。采取上述处理思路进行网格划分，结果见图6。

图6 某一段桨叶的网格模型

由于需要将划分的网格导入到ADINA中进行分析计算，而当前Hypermesh软件没有ADINA求解器的定义模板，因故将上述网格模型保存为nastran网格文件，即nas格式［2］。

3 桨叶结构的应力应变分析

锥形混合器的工作过程实质上是一个动态的流固耦合过程，但是针对锥形混合器的桨叶结构的受力情况，在本文的假设条件下，可以认为是一种线性的静力分析。

静态载荷作用下的结构需要求解的有限元方程可以表示为［3］：

式中，K为结构的刚度矩阵（各个单元刚度矩阵的组合），矢量u为位移向量，而P则为作用在结构上的载荷向量，此方程实质上是外力和内力的平衡方程。平衡方程可以通过直接求解法和迭代求解法进行求解，ADINA软件默认的求解器是稀疏矩阵求解器，当然也可以选择直接求解器，直接求解器的原理是位移未知量使用高斯消去法求解，利用刚度矩阵K的稀疏性和对称性提高软件的计算效率，具有稳健、正确、高效的特点，非常适用于求解规模较小的分析问题［2，3］。本文采用直接求解法进行计算。

通过式（1）得到节点位移后可以通过材料的本构关系计算单元应力，对于线性静态分析可以使用胡克定律计算应力，胡克定律可以表示为：

上式中，应变ε是位移的函数，C是材料的弹性矩阵。

3.1 求解计算的相关设定

将在Hypermesh中划分得到的nas格式网格文件导入到ADINA中进行材料的定义、边界条件的设定、定义求解计算等。

本文根据工作实际中进行搅拌混合的物料的密度以及桨叶实际转速，估算出载荷的大小，并将其施加桨叶上进行线性静态分析，此时可以认为桨叶转轴被全约束［4］。

导入ADINA－AUI中，对桨叶转轴添加全约束的网格模型见图7。

图7 施加了约束的网格模型

双螺锥形混合器桨叶材料一般为304不锈钢，因此定义材料特性为各项同性材料，杨氏模量为2.07e11MPa、泊松比为0.3、密度为7 930kg／m3。

采用施加压力的方式定义载荷，根据实际工作过程中载荷的作用特点，将其分解为一个轴向载荷和一个切向载荷分别施加在桨叶上（图8、9）。

图8 施加轴向载荷

图9 施加切向载荷

3.2 求解结果及其分析

计算结束后，在Post－Processing模块中打开结果文件可以得到桨叶的应力及位移结果云图（图10）。

图10 桨叶的应力及位移结果云图

由图10可以看出，桨叶受到的最大应力为20 251pa，发生在桨叶的根部，而桨叶叶片的最边缘处位移变形较大，最大变形位移为5.183×10－5。由于304不锈钢的屈服极限大概在205MPa左右，所以还不会造成破坏，但是可以看出在设计桨叶时对桨叶根部的处理（比如焊接的焊缝等）是很重要的，另外叶片如果变形太厉害将严重影响桨叶的工作效率，所以桨叶边缘的应变量也是我们在进行桨叶设计时必须重点考虑的问题。