图解法SVPWM 过调制控制

尹国慧，罗建武，王 杰，王洪涛

(东风汽车集团股份有限公司，湖北武汉100089)

0 引 言

新能源车载永磁电驱动系统通常采用的空间矢量脉宽调制(SVPWM)策略具有较高的系统效率和电流控制精度，且便于实现数字化;由于永磁同步电机系统输入直流电压的限制，导致电压利用率的高低直接影响到永磁同步电机系统高速弱磁运行区间的宽度，限制了车辆调速性能。传统SVPWM 控制电压利用率有限，理论上最高调制比可以达到1，采用过调制控制策略后，可进一步提高新能源车载永磁同步电机电驱动系统的电压利用率，从而提高永磁同步电机系统高速弱磁运行区间的宽度。文献［1］提出了根据调制方式的不同，将调制区分成线性调制区、过调制Ⅰ区和过调制Ⅱ区，并推导出了各区的调制算法;文献［2］分析推导了这种算法，但其实现过程繁琐，难以操作;文献［3］将整个控制区(包括线性调制区和过调制区)统一为一种控制模式，算法更简单，但输出电压的谐波含量比较高;文献［4］提出了一种动态电压过调制算法，但其实现复杂，对电机参数依赖程度高，不利于工程应用。文献［5］中SVPWM 过调制控制I 区调制法，以相邻矢量作用时间是否大于周期值为进入过调制控制的依据，对相邻矢量的工作时间进行限幅，虽然算法简单，应用较广，但因输出电压基波幅值小于给定电压矢量，从而引起的输出电压控制规律非线性，降低了电流环PI 调节器性能，造成定子电流不稳定，甚至出现振荡。

本文在简要分析SVPWM 控制原理的基础上，详细推导了SVPWM 过调制控制方法，并结合ISG电驱动系统是闭环控制系统这一特点，给出闭环磁场定向控制下的SVPWM 过调制控制策略，该策略旨在使ISG 电驱动系统在闭环控制下电压利用率最大。

1 SVPWM 调制原理

三相桥式电压型逆变器如图1 所示，以“1”表示任意桥臂的上管导通、下管关闭，则逆变器状态(VT5、VT3、VT1)的开关组合［6］一共有八种不同的组合，即可以输出八个基本电压矢量，这其中有六个非零矢量(U1～U6)和两个零矢量(U0、U7)，其定义如图2 所示。

图1 三相电压型逆变器

图2 SVPWM 矢量图和区间划分

SVPWM 调制的原则是一个PWM 工作周期内的电压矢量平均值相等。即在一个扇区内，通过相邻基本电压矢量的组合工作，使合成电压矢量平均值与给定电压矢量相等。假定给定电压矢量U，与其相邻的两个基本电压矢量分别为Ui和Ui+1，则U可以用Ui和Ui+1组合得到:

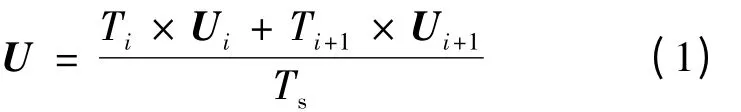
式中:Ti为基本电压矢量Ui作用时间;Ti+1为基本电压矢量Ui+1作用时间;Ts为一个PWM 开关周期;U 为逆变器输出电压矢量。

在传统的正弦调制方法中，合成给定电压矢量的3 个基本电压矢量的作用时间可由下式计算:

式中:T0为零矢量作用时间;θ 为Ur与Ui夹角;Udc为直流母线电压;Ur为给定电压矢量。

定义调制比M:

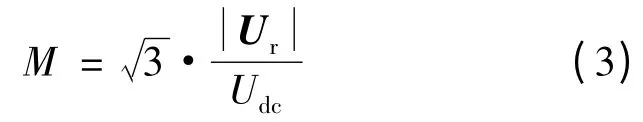
式中:Ui为给定电压矢量;Udc为直流母线电压。

在SVPWM 控制中，逆变器通过6 个开关管的开关组合，使合成电压矢量在矢量空间中沿着以给定矢量为半径的圆旋转，逆变器输出幅值相同，相位互差120°的三相正弦交流电。根据SVPWM 控制原理，合成电压矢量轨迹必须要在U1～U6为顶点的正六边形内，所以，采用正弦SVPWM 矢量控制时，合成电压矢量的最大幅值为正六边形的内切圆半径，如图2 中的圆所示，即采用上述调制算法时，最大调制比为1。

2 SVPWM 过调制控制原理

当调制比超过1 时，就进入SVPWM 过调制状态。此时，给定电压矢量Ur的幅值超出正弦SVPWM 调制矢量的最大值，超过了六边形内切圆边界(如图3 中圆c)，此时，逆变器实际输出的电压矢量会比给定的电压矢量小，因此需要采用SVPWM 过调制控制，使逆变器输出的电压矢量与给定电压矢量相等。SVPWM 过调制控制以输出电压基波相等［7］为原则，在正六边形范围内对给定电压矢量进行调整，在一个扇区内，保证调整后的电压矢量平均值与给定矢量相等。

图3 过调制方式矢量图

当调制比M 较小时，仅通过对超过正六边形边界的给定电压矢量幅值进行截短，不改变其频率及相位，便可实现调整后的电压矢量平均值与给定矢量相等，此区间定义为过调制方式Ⅰ区;当调制比M较大时，要同时调整给定电压矢量的幅值和相位才能调整后的电压矢量平均值与给定矢量相等，此区间定义为过调制方式Ⅱ区。

过调制方式Ⅰ的空间电压矢量如图3(a)所示。图中曲线b 为给定电压矢量，对给定电压矢量Ur超出正六边形部分的区域进行调整，减小其幅值，使其落在正六边形的边界上，增大未超过正六边形边界的给定电压矢量Ur的幅值，保证在一个扇区内逆变器输出合成电压矢量平均值和给定电压矢量Ur相等。在一个扇区内与给定电压矢量相邻两个基本电压矢量Ui和Ui+1及零矢量的作用时间分别:

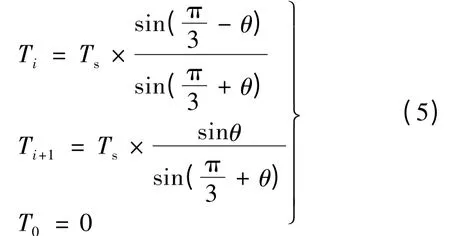
式中:Ti为Ui作用时间;Ti+1为Ui+1作用时间;Ts为逆变器的开关周期;U 为输出电压矢量;T0为零矢量作用时间。

采用过调制控制后，给定的电压矢量由Ur变为调整后的给定电压矢量U，调整后的电压矢量运行轨迹为图中的折线ABCD，逆变器输出电压矢量U平均值与Ur相等，在整个调制过程中U 和Ur始终同频同相。

过调制控制方式Ⅱ的空间电压矢量如图4 所示。在一个扇区中，调整后的电压矢量U，先保持为基本电压矢量Ui;当α≤θ ＜时，U 以小于ω 的转速旋转，沿正六边形边沿移动;当π 6 ≤θ ＜－α 时，U 以大于ω 的转速旋转，沿正六边形边沿移动;当－α≤θ ＜时，电压矢量U 保持为扇区另一基本电压矢量Ui+1。各基本电压矢量Ui、Ui+1及零矢量的作用时间:

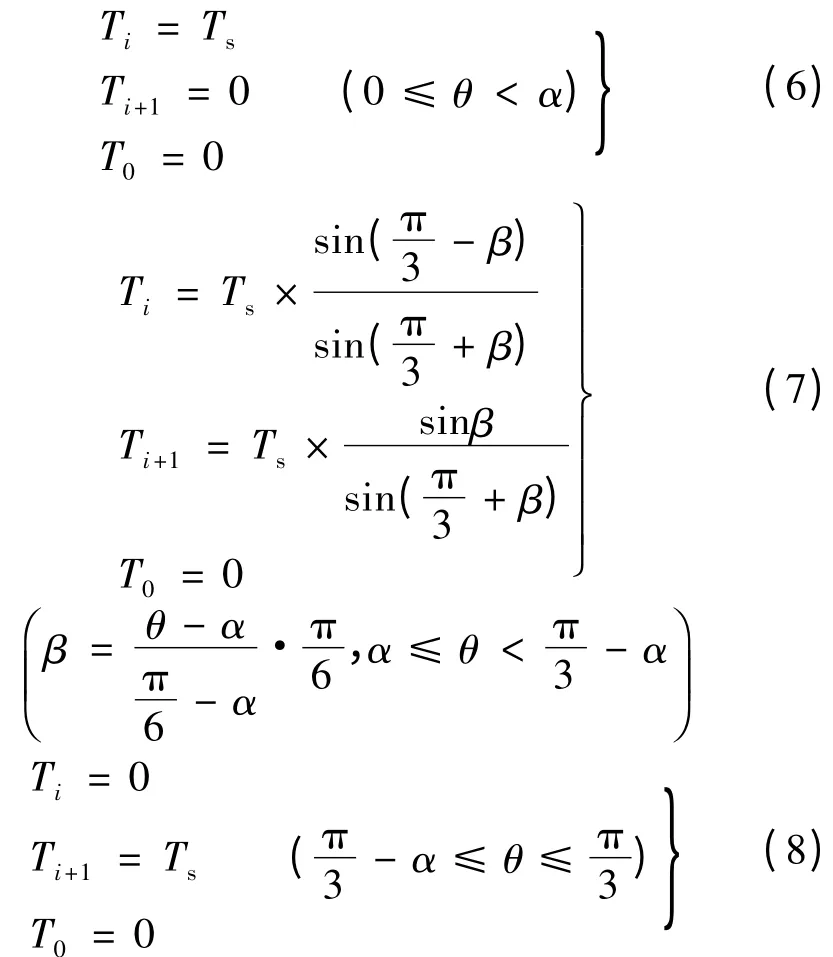
式中:Ti为Ui作用时间;Ti+1为Ui+1作用时间;Ts为逆变器的开关周期;U 为输出电压矢量;T0为零矢量作用时间。

在该过调制控制区域内，给定电压矢量调整矢量U 与给定电压矢量Ur的频率与相位均不同，在正六边形各顶点会处于停顿状态。随着过调制程度的加深，最终逆变器依次输出六个非零基本电压矢量，处于方波输出(纯六拍)状态，其电机定子磁链矢量按正六边形旋转［8］。

3 图解法SVPWM 过调制控制方法

采用过调制控制后，各基本电压矢量作用时间的运算变得复杂，而其中关键的是控制角α 的准确计算。根据SVPWM 调制原则，逆变器输出电压矢量平均值应该与原给定电压矢量相等，且在过调制区间，对于同一扇区，U 与Ur的平均旋转速度相同，即实际电压矢量U 围成的多边形面积与Ur围成的扇形面积相等。

过调制方式Ⅰ区:

结合式(3)得:

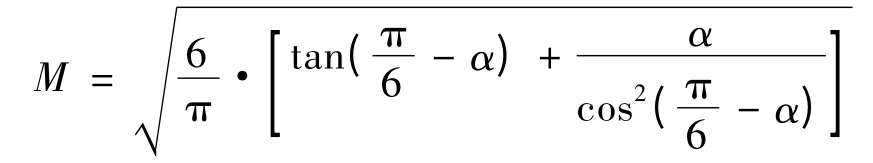
式中:Ur为给定电压矢量;Sr为围成的扇形面积;SOABCD为U 围成的多边形面积。

过调制方式Ⅱ区:

结合式(3):

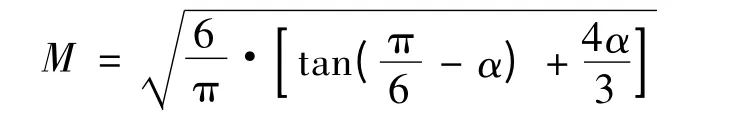
式中:Ur为给定电压矢量;Sr为Ur围成的扇形面积;SOABCDEF为U 围成的多边形面积。

以上论述的SVPWM 过调制控制方法，可保证输出电压基波值与给定电压值相等，从而保证逆变器从正弦调制线性过度到过调制，最终实现六拍运行。

在实际应用中，可按式(9)、式(10)预先在CPU中存储过调制控制角α 与调制比M 的映射表，过调制区间Ⅰ与过调制区间Ⅱ中M 与α 的曲线如图4、图5 所示，采用查表法来确定当前调制比M 对应的过调制控制角α，就可以按上述的过调制控制方法进行控制。

图5 过调制Ⅱ区M与α 的映射曲线

图4 过调制Ⅰ区M与α 的映射曲线

4 SVPWM 过调制仿真分析

电机模型为Y 型三相永磁同步电机，极对数为6，额定电压144 V，额定功率10 kW，额定转速2 500 r /min;采用RMxprt建立的永磁同步电机本体模型与Simplorer 建立的ISG 电机控制系统进行联合仿真。电机转速2 500 r/min，当控制系统的调制比M从1 变化到1.154 时，电机相电压线性由正弦波过渡到方波，如图6 所示。对传统SVPWM 矢量控制与SVPWM 过调制控制下的ISG 电驱动系统外特性进行对比仿真，仿真的扭矩外特性如图7 所示。

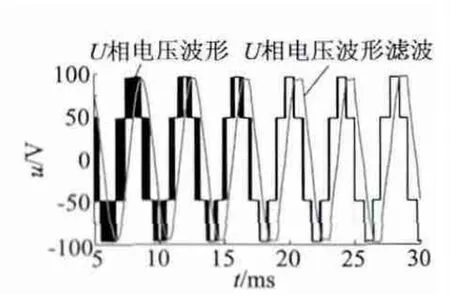
图6 M 由1 变化到1.154 时U 相电压波形

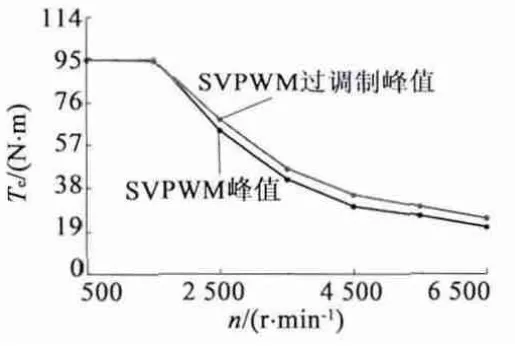
图7 不同控制方式下的扭矩外特性

5 结 语

本文提出的SVPWM 过调制控制方法仅需在CPU 中预先存入过调制控制角α 与调制比M 的映射表，就可以控制逆变器从传统正弦SVPWM 调制线性过渡到SVPWM 过调制，最终实现六拍运行。仿真数据说明，对于相同的永磁同步电机模型，在高速弱磁运行区间，本文提出的SVPWM 过调制控制方法相对于传统SVPWM 控制的优点是:SVPWM 过调制控制的电压利用率从1 提高到1.154;峰值输出扭矩提高了3 ～7 N·m，大大提高了永磁电驱动系统的调速运行区间宽度;缺点是SVPWM 过调制控制的扭矩脉动和系统噪声加大，系统效率也相应下降，对系统的散热能力要求提高。

［1］ Holtz J，Lotzkat W K，Hambadkone A M.On continuous control of PWM inverters in the overmodulation range including the six－step mode［J］. IEEE Transactions on Power Electronics，1993，8(4):546－553.

［2］ Dong－Choon L M，Young L G.A novel overmodulation technique for space－vector PWM inverters［J］.IEEE Transactions on Power Electronics，1998，13(6):1144－1151.

［3］ Bolognani S，Zigliotto M. Novel digital continuous control of SVM inverters in the overmodulation range［J］. IEEE Transactions on Industry Applications，1997，33(2):525－530.

［4］ Bon－Ho B，Seung－Ki S.A novel dynamic overmodulation strategy for fast torque control of high－saliency－ratio AC motor［J］.IEEE Transactions on Industry Applications，2005，41(4):1013－1019.

［5］ 全恒立，张钢，陈杰，等.一种SVPWM 过调制算法的数字化实现.电气传动，2010，40(5):44－48.

［6］ Arulmozhiyal R，Baskaran K.Space vector pulse width modulation based speed control of induction motor using Fuzzy PI controller［J］.IEEE International Journal of Computer and Electrical Engineering，2009，1(1):1793－8198.

［7］ 张立伟，刘钧，温旭辉，等.基于基波电压幅值线性输出控制的SVPWM 过调制新算法［J］.中国电机工程学报，2005，25(19):12－18.

［8］ 梁振鸿.PWM 过调制技术在电动汽车用永磁同步电机控制中的应用［D］.北京:中国科学院研究生院(电工研究所)，2002.