基于力学及电学性能的汽车发电机转子爪极尺寸优化选择

吴 锋，鲍晓华，刘谋志，李佳庆

(合肥工业大学，安徽合肥230009)

0 引 言

汽车发电机是用来对蓄电池进行充电和为汽车上各种用电设备提供所需的电能，随着汽车工业的发展，汽车发电机也有着持续的发展和改进。汽车发电机是一种有着爪极转子结构的凸极同步电机，与一般凸极式交流发电机不同，其中所用三相同步发电机的磁场是采用鸟嘴形磁极，这种磁极可以使定子感应的交流电动势近似于正弦曲线。汽车发电机定转子间隙通常只有0.25 mm ～0.4 mm。在电机运行过程中转子的变形可能导致定转子相撞，使电机造成破坏，所以如何减少爪极转子变形成为汽车发电机设计中的关键环节。

随着各种汽车的普及，对汽车发电机的性能要求也越来越高。近年来，国内外有不少专家学者对汽车发电机进行了优化设计，文献［1］从汽车爪极发电机电磁有限元仿真出发，通过电机参数样本空间设计，利用支持向量机对其电磁模型进行非线性回归分析，并用遗传算法对其结构参数进行优化［2］。漏磁是汽车爪极发电机效率低的主要原因，基于此提出混合励磁转子，通过非参数建模和智能最优算法来得到最小漏磁的目标结果，并用自制混合励磁爪极交流发电机试验平台检验理论分析的正确性。文献［3］设计了一种混合励磁爪极皮带式起动发电机，通过在爪极间镶嵌磁钢来减小爪极间漏磁，提高电机功率密度和低速输出能力，采用磁路法和三维有限元法分析了其电机结构和原理，基于机械、模态和热工多领域综合仿真分析方法解决高密度电机极限能力分析与优化设计。文献［4］应用三维刚粘塑性有限元显式算法对磁极精锻成形过程进行了模拟分析，得出了变形中材料的流动状态和等效塑性应变分布规律，从而对磁极精锻成形工艺参数、模具结构进行了优化设计。文献［5］推出集总参数耦合电路模型的爪极发电机，定义一个三维傅里叶级数表征空气隙磁通密度来导出该模型，包括转子凸极、定子绕组、定子槽导致的谐波级数展开，该模型对运用电路模型分析程序的交流发电机仿真中得到应用，并比较试验结果证明该模型理论的正确性。迄今为止，还缺乏针对汽车发电机同时兼顾力学及电学性能的研究。

本文着重分析气隙磁场中转子爪极在电磁激振力与转子旋转离心力的共同作用下的变形分布，为提高汽车发电机的输出性能，对其爪极尺寸进行基于电磁与力学性能的优化设计。通过改变不同爪极厚度轴向角结构，将转子爪极等效为悬臂梁模型进行分析计算，求出在不同爪极厚度轴向角下爪极的最大挠度，运用Ansys 有限元分析来验证不同爪极厚度轴向角时爪极的位移变形分布，并且运用Maxwell 3D 软件比较不同β 角时的电势波形及效率的变化，进而得出最佳的爪极厚度轴向角。

1 汽车发电机转子爪极模型及等效悬臂梁模型

汽车爪极发电机的转子模型如图1 所示。其中电机的磁路由电机定子、转子爪极及爪极与励磁绕组间的空间部分组成，在这些不同的部分其磁导率是不同的。主磁通路径是励磁电流产生轴向磁通经转子磁轭到达爪极，然后转子将轴向磁通转换为径向磁通，接着经气隙、定子齿、定子磁轭到达另一个极，再经过另一个极下的定子齿、气隙和爪极，回到转子磁轭。这样就形成一个闭合回路［6］。所述爪极结构如图1 所示。

图1 汽车发电机转子结构实物图

因为汽车发电机转子爪极是成对称圆周分布的，故将转子中取出一个爪极模型进行分析即可。汽车发电机爪极模型如图2 所示。

图2 中，DR为爪极转子外径;l 为爪极长度;h1为极尖厚度;h2为极根厚度;bmin为爪尖部分的宽度;bmax为爪根部分的宽度;θ 为爪极侧面斜角;β 为爪极厚度轴向角，这也正是本文的重点研究对象，即基于最大挠度的大小对β 角进行优化。

图2 汽车发电机爪极模型

汽车发电机的爪极在受到气隙磁场径向力以及离心力共同作用下发生变形，其变形主要体现在爪极尖部，而根部的形变可忽略不计，因而可将爪极等效为悬臂梁模型来分析计算。汽车发电机爪极等效的悬臂梁模型如图3 所示。

图3 汽车发电机爪极等效的悬臂梁模型

2 汽车发电机爪极受力分析及优化角的取值范围

2.1 发电机定子铁心与转子爪极之间气隙磁场径向力分析

气隙中存在的一系列定、转子磁场之间的相互作用，可以产生数量很多的电磁力波。根据麦克斯韦定律，在电机气隙中单位面积径向电磁力［7］的瞬时值可表示:

式中:b2(θ，t)为气隙磁密;μ0为空气磁导率。

在气隙磁场所产生的力波中，当主波磁场产生的力波起主导因素，在爪极所受的气隙磁场径向力中可以等效为主波磁场产生的力波。

主波磁场所产生的力波可表示:

其中:

p0是径向力的不变部分，它是在定子圆周上均匀分布的力系，使定子铁心受到压缩应力，因为不论它是N 极还是S 极，它总是受到来自转子对它的吸力。

作用在定子轭平均半径圆柱表面上单位径向力的幅值prav，可由气隙中的单位面积径向力幅值按下式求得:

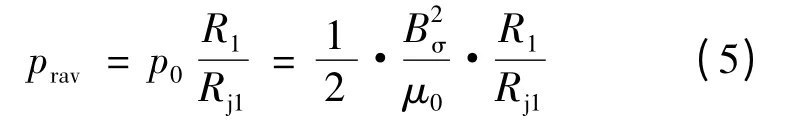
式中:R1为定子内圆半径;Rj1表示定子轭的平均半径;Bσ为气隙磁密。

2.2 爪极所受离心力分析

汽车发电机转速一般都很高，而离心力的大小与转速的平方成正比，以本文所研究的14 V/1 kW汽车发电机为例，工作转速为1 300 ～18 000 r/min，额定转速为6 000 r/min，在这么高转速下爪极所受的离心力［8］大小是比较大的，其公式:

式中:F1为离心力，单位为N;m 为爪极质量，单位为kg;ω 为爪极转速，单位为rad/s;R 为旋转半径，单位为m。

2.3 爪极厚度轴向角β 的取值范围

爪极的特点之一是通过任一截面的磁通不相等。例如在图4 中，设距离爪尖x 处的αα'平面的截面积为Sx，如果认为气隙磁场［9］轴向均匀分布，爪根截面的磁通为ΦU0，则通过Sx截面的磁通:

磁通密度:

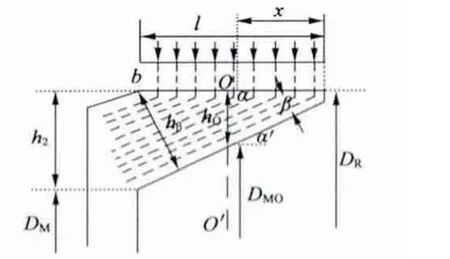
图4 穿过爪极任一截面的磁通

其中，OO'为轴向中心线，l 为爪极长度，DR为转子外径，爪根部分的计算高度为h2，有效高度为hβ，可得:

若设爪极根部的允许磁通密度为BR，根部截面积为SR，则爪根的最小截面积:

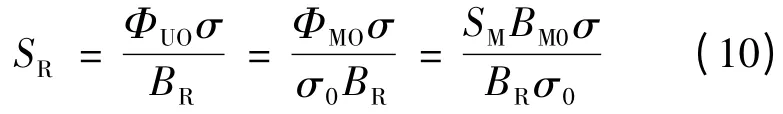
若爪极平均爪宽为b，则SR=bhβ，代入(9)式后得:

再计算结构上可能达到的最大β 角。从转子径向尺寸出发，由图4 可得:

从转子切向尺寸出发，在图4 中，取轴向中心线OO'处的爪厚为h2O。h2O随β 角的增大而增加;当h2O增大到某一值时，相邻异极爪子的内侧将相互接触，如图5 所示。

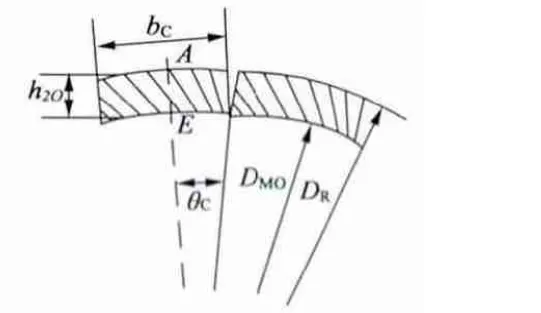
图5 爪极极间尺寸

利用三角运算，可以求出当h2O达到极限值时的β:

因为β 要同时满足径向和切向两个条件，故比较式(13)和式(14)，取其较小值为β 的最大值βmax。

3 将爪极等效为悬臂梁模型进行挠度分析计算

将爪极爪臂等效为悬臂梁［10］模型进行受力分析，如图3 所示。在爪臂上建立直角坐标系，在横坐标x 处取微小单元dx，其等效爪臂宽度为b(x)，厚度为h(x)，在dx 所处的微元表面受到的等效集中力为F(x)，可得:

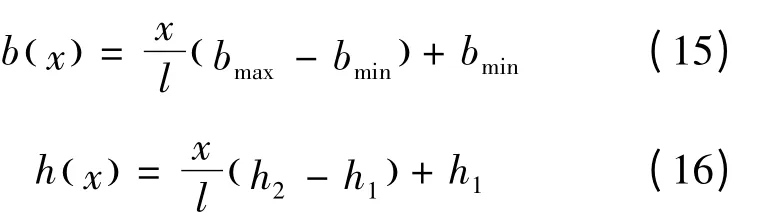
由式(5)可得，气隙主波磁场对爪臂单位面积产生的径向力幅值:

由式(6)可得，在旋转过程中所引起的离心力对爪臂单位面积产生的幅值:

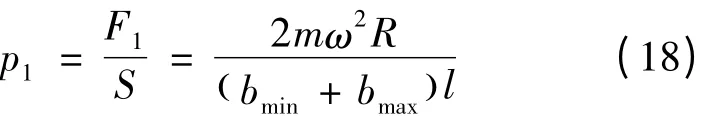
从而可得:

令:

则单位长度所受力的大小:

将q(x)分解成线性部分q1(x)，如图7 所示。常数部分q 如图8 所示，其中:

图6 爪臂单位长度所受力的线性部分

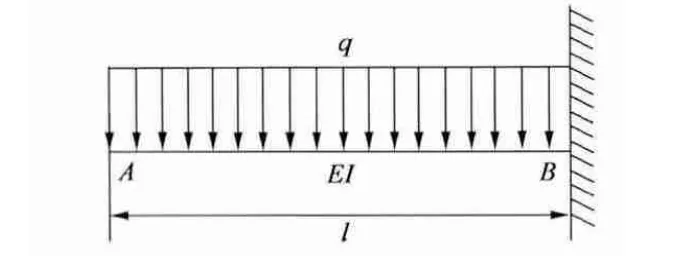
图7 爪臂单位长度所受力的常数部分

由q1(x)所引起的最大挠度值:

式中:q 为固定端单位长度受力大小;E 为材料的弹性模量;I 为固定端截面的惯矩:

由q 所引起的最大挠度值:

将q1(x)和q 引起的最大挠度值进行叠加可得总体最大挠度值:

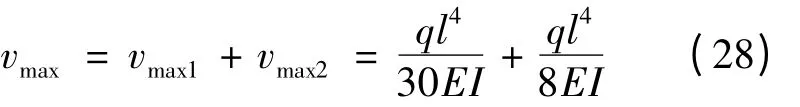
将式(28)进行整理可得:

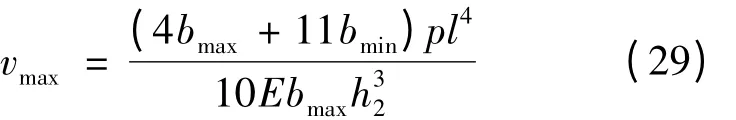
根据图3 可算得:

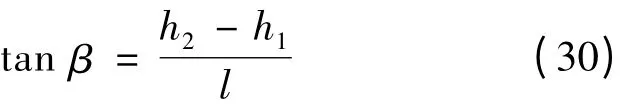
爪臂总体积:

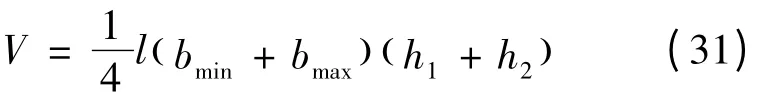
在保持爪臂用料不变即体积不变的情况下，同时保持爪极表面尺寸不变，即保持bmin、bmax和l 不变时，此时h1+h2保持不变，通过改变h1及h2的大小来改变β 角度，从而找到合适的β，让爪臂的挠度尽可能小。

由式(30)和式(31)可得:

将式(31)代入式(28)可得:

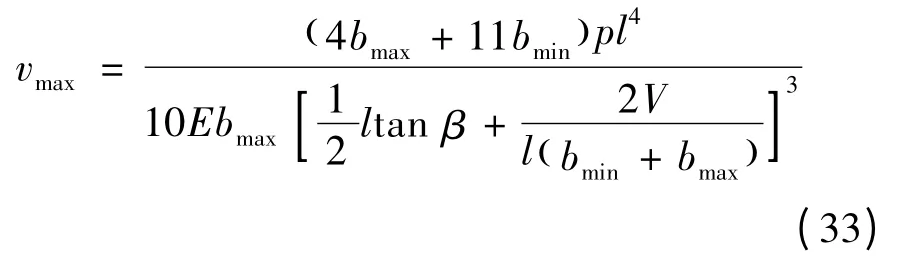
由上式可知，当β 在(βmin，βmax)范围内取适当值时，爪臂的最大挠度随着β 的增大而减小。

4 基于爪极尺寸变化的汽车发电机爪极力学及电学性能仿真分析

4.1 汽车发电机爪极挠度［11］Ansys 仿真分析

本文选择14 V/1 kW 常规汽车发电机为研究对象，其定子外径R0=114 mm，定子内圆半径R1=90.2 mm，表示定子轭的平均半径Rj1=110.6 mm，气隙磁密Bσ=0.443 8 T，气隙长度δ =0.3 mm，转子外径R=89.9 mm，电机的额定转速ω =6 000 r/min = 628.3 rad/s。通过计算爪极臂的重量m =V·ρ =0.022 36 kg，爪极顶部表面积S =4. 495 ×10－4m2。转子爪极单位面积所受径向力幅值:

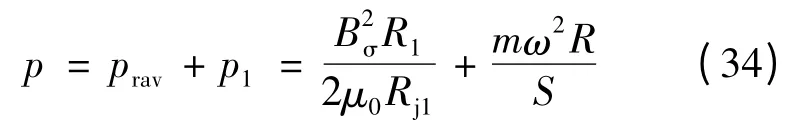
通过计算可得p=1.829 MPa。用Ansys 对该电机爪极进行有限元分析［12］，其中气隙磁场径向力作为分布力载荷，爪极所受离心力转化为对爪极表面的压强进行分析。将整个爪极作为悬臂梁模型，爪根部分进行相应约束，分析爪臂部分的位移变形情况，从而得出爪臂部分最大挠度值。

爪极在受到气隙磁场径向力和旋转离心力共同作用下爪臂的位移变形图如图8 所示。

图8 爪臂的位移变形图

由图8 可知，在不改变β 角大小时，爪臂最大位移集中在爪尖部分，即爪臂最大挠度为vm=0.290×10－4m =0.029 mm，与气隙长度δ =0.3 mm 相比，变化了9.7%。

在保持爪极用料不变时，可知h1+ h2为固定值，文中所研究的对象其h1=3.8 mm，h2=9.7 mm。通过改变h1及h2尺寸可以得到最大挠度变化如表1 所示。

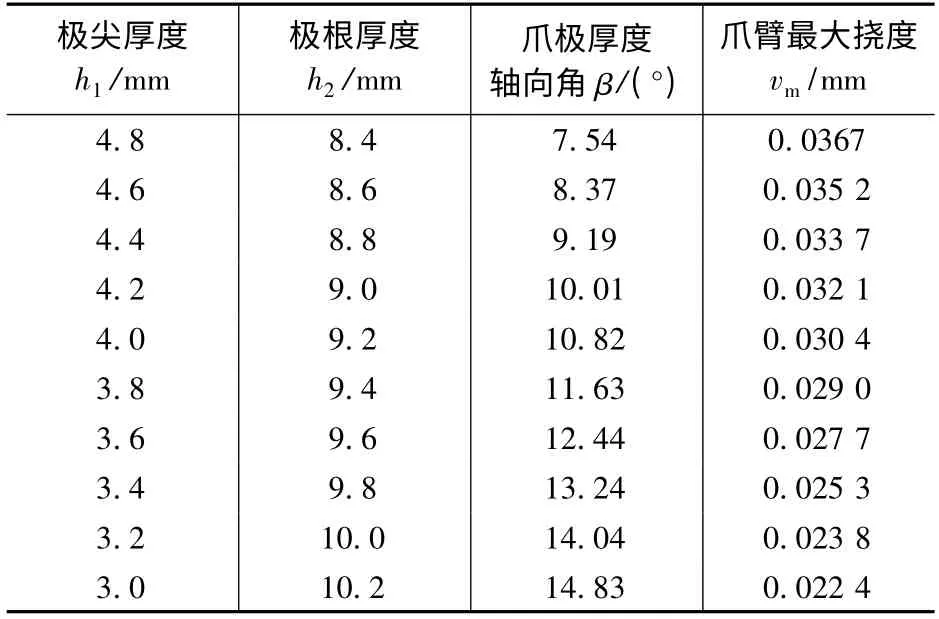
表1 保持相同用料时爪极的尺寸及最大挠度变化

4.2 不同爪极厚度轴向角对应感应电势及效率的变化

利用Maxwell 3D 软件建立电机三维有限元电磁场分析模型，比较不同β 角时的感应电势波形及效率［13］的变化。

图9 为感应电势基波和6 次谐波随着爪极厚度轴向角变化而变化的曲线。

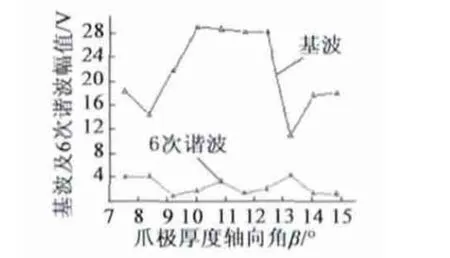
图9 感应电势基波和6 次谐波与爪极厚度轴向角的变化关系

由图9 可知，当爪极厚度轴向角β 处在10.01°～10.82°之间时，感应电势基波分量达到最大值。当爪极厚度轴向角β 处在9.19° ～10.01°之间时，感应电势6 次谐波分量达到最小值，而汽车发电机中输出电磁噪声［14］主要是电磁场谐波次数，它是转速的6 倍，即感应电势6 次谐波分量越小，输出的电磁噪声也越小。综上可得，当β =10.01°时，感应电势基波及6 次谐波都可达较理想的效果。

由图10 可知，其效率是随着β 的增大略有增加，在所选计算值中，效率最大为53.983 7%，最小为53.977%，其效率变化较小。

图10 效率与爪极厚度轴向角的变化关系

5 结 论

本文通过分析计算汽车发电机爪极轴向厚度角的变化，可得以下结论:

(1)在保证爪极体积不变的情况下，适当增加爪极厚度轴向角β，即爪臂极根厚度增加，可以减小挠度大小。

(2)爪极厚度轴向角β 的增大势必会造成气隙磁密及感应电势的变化。当爪臂极根厚度h2=4.2 mm，即β=10.01°，可以让感应电势基波和6 次谐波处于最佳的幅值。

(3)在保持爪极体积不变的情况下，其效率随爪极厚度轴向角β 的增大而略有增加。

［1］ 鲍晓华，王群京，倪有源，等.基于支持向量机和遗传算法的爪极发电机建模及参数优化［J］.电工技术学报，2006，21(4):57－61.

［2］ Bao Xiaohua，He Qingling，Wang Qunjing，et al.Research and optimal design on hybrid excitation claw－pole alternator for automobile application［J］. International Conference on Electrical Machines and Systems，2008:3493－3496.

［3］ 李维亚，黄苏融，张琪.混合动力车用混合励磁爪极皮带式起动发电机多领域仿真分析［J］. 中国电机工程学报，2010，30(36):7－15.

［4］ 高永超，华林，赵玉民，等. 汽车发电机磁极精锻成形三维有限元模拟和工艺优化［J］.中国机械工程，2005，16(12):1110－1113.

［5］ Pekarek S D，Tichenor J，Eversman W，et al.Analytical derivation of a coupled－circuit model of a claw－pole alternator with concentrated stator windings［J］. IEEE Transactions on Energy Conversion，2002，17(1):32－38.

［6］ 王群京，倪有源，姜卫东，等.汽车用爪极发电机负载磁场和电感的分析与计算［J］.中国电机工程学报，2004，24(3):91－95.

［7］ Yamada T，Fujisaki K.Basic characteristic of electromagnetic force in induction heating application of linear induction motor［J］.IEEE Transactions on Magnetics，2008，44(11):4070－4073.

［8］ Asama J，Amada M，Tanabe N，et al. Evaluation of a bearingless PM motor with wide magnetic gaps［J］.IEEE Transactions on Energy Conversion，2010，25(4):957－964.

［9］ Lubin T，Mezani S，Rezzoug A. Exact analytical method for magnetic field computation in the air gap of cylindrical electrical machines considering slotting effects［J］.IEEE Transactions on Magnetics，2010，46(4):1092－1099.

［10］ Littrell R，Grosh K. Modeling and characterization of cantilever－Based MEMS piezoelectric sensors and actuators［J］. Journal of Microelectromechanical Systems，2012，21(2):406－413.

［11］ Dong－Kil Shin，Jung Ju Lee. Theoretical analysis of the deflection of a cantilever plate for wirebonding on overhang applications［J］.IEEE Transactions on Components，Packaging and Manufacturing Technology，2012，2(6):916－924.

［12］ Tessarolo A，Agnolet F，Luise F，et al.Use of time－harmonic finite－element analysis to compute stator winding eddy－current losses due to rotor motion in surface permanent－magnet machines［J］. IEEE Transactions on Energy Conversion，2012，27(3):670－679.

［13］ Frosini L，Bassi E.Stator current and motor efficiency as indicators for different types of bearing faults in induction motors［J］.IEEE Transactions on Industrial Electronics，2010，57(1):244－251.

［14］ He Guhuan，Huang Zhenyu，Qin R，et al.Numerical prediction of electromagnetic vibration and noise of permanent－magnet direct current commutator motors with rotor eccentricities and glue effects［J］.IEEE Transactions on Magnetics，2012，48(5):1924－1931.