静止状态下异步电动机参数离线辨识方法

戴 亮，黄志远，陈业明，王 真，张东宁

(中国电子科技集团第二十一研究所，上海200233)

0 引 言

异步电动机矢量控制中需要的电机参数在电机铭牌中查不到，甚至许多电机生产厂家都不会刻意对这些参数进行检测计算。因此，电机参数辨识一直是电机控制领域中一个较重要的课题。电机参数辨识包括离线参数辨识和在线参数矫正两部分。离线参数辨识是指在电机运行之前，对其施加一系列激励信号，通过检测电机响应来获得电机相关参数［2］。一般通用变频器的电机参数自整定功能，采用的是传统的离线辨识方法，需要对电机进行堵转试验和空转试验。但对于部分大功率电机而言，上述两个实验都难以进行。首先，大功率电机力矩较大，难以人为锁住输出转轴，堵转试验实现困难;其次，大功率电机在系统调试前通常已经与负载固定安装，基本属于不可拆卸或拆卸难度很大的状态，所以空载试验也难以进行。鉴于这种情况，根据电机应用的制约条件，本文给出一种电机静止状态下的离线参数辨识方法，该方法还考虑了变频器输出参考电压与实际电压不一致的情况以及集肤效应的影响，对其进行了补偿，进一步提高了参数辨识的准确性。

1 电机参数传统离线辨识方法

图1 是归一化到定子侧的异步电机单相绕组等效电路图。图中，Us、Is表示定子单相电压和电流，Rs表示定子电阻，Lσs表示定子漏感，Rr表示归一化到定子侧的转子电阻，Lσr表示归一化到定子侧的转子漏感，Lms表示定转子互感。其中RS、Lσs、Rr、Lσr、Lms即为矢量控制中需要检测的电机参数。传统辨识方法中采用直流试验获取定子电阻Rs，采用堵转试验获取转子电阻Rr、定子漏感Lσs和转子漏感Lσr，采用空转试验获取定转子互感Lms［3］。

图1 单相绕组等效电路图

2 静止状态下电机参数离线辨识方法

异步电动机在静止状态的参数离线辨识方法同样是通过三个试验方法对上述五个电机参数进行检测。第一，辨识定子电阻，传统辨识方法中的直流试验是一种静态试验，所以本方法沿用该方案，并补偿变频器输出参考电压与实际电压误差对辨识精度的影响;第二，辨识转子电阻、定子漏感和转子漏感，用单相高频交流试验方法替代传统的堵转试验，并采取措施，削弱集肤效应对转子电阻辨识精度的影响［4］;第三，辨识定转子互感，采用单相低频试验方法进行。下面对上述三个试验方法进行详细说明。

2.1 定子电阻参数辨识

定子电阻通过直流试验方法进行辨识，在定子电阻中通入直流激励电压，电感相当于短路，其单相绕组等效电路如图2 所示。对绕组中的相电压和相电流进行检测，即可计算出该相的定子电阻。

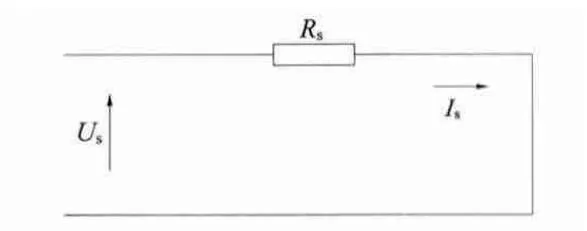
图2 直流试验单相绕组等效电路

在变频器中使用该方法时，由于没有输出电压检测回路，需要用输出电压参考值来替代实际值。而三相桥输出电压时，由于存在开关管开通和关断延时时间、管压降以及死区时间等因素，导致参考电压和实际电压之间有较大误差。特别是输出电压较低的时候，该误差会对辨识精度造成严重影响。为解决该问题，本文采用增量计算的方法来辨识定子电阻。根据输出电压参考值和实际值的误差来源，对电机绕组施加两次相近幅值的直流电压，其误差量大小基本不变，此时检测两次直流试验的输出电压和电流增量，计算出定子电阻Rs，即可较好地避免该误差量对辨识精度的影响。定子电阻的计算公式如下:

式中:U1、U2分别表示前后两次直流电压参考值;I1、I2分别表示前后两次直流电流的检测值。最后对其他两相绕组进行辨识，取三次辨识的平均值即可作为矢量控制用电机参数值。

2.2 定子漏感、转子电阻、转子漏感参数辨识

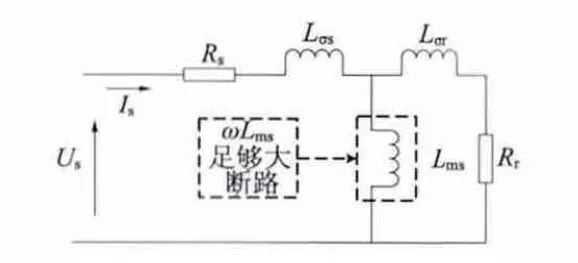
图3 单相高频交流试验单线绕组等效电路

在单相高频交流试验中，用功率计检测出单相线圈中的电压、电流有效值和有功功率值，即可进行计算。在变频器中使用该方法时，无法直接检测到功率值，可以检测到电压、电流瞬时值及其相位差，由此求得电压有效值Us、电流有效值Is和功率因数值cosφ，从而计算转子电阻、定子漏感和转子漏感三个参数。如下:

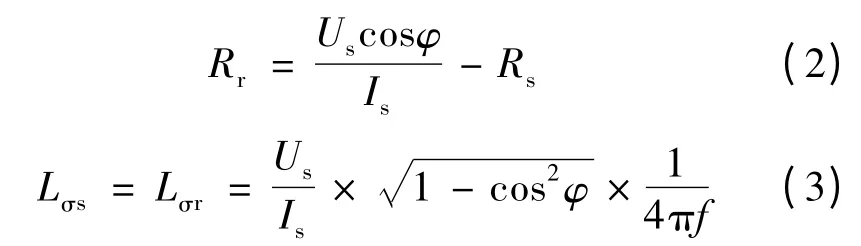
关于漏感Lσ，在实际电机定子侧和转子侧是不同的，但都远小于互感Lms，所以在控制上近似认为定子漏感和转子漏感是相等的。

单相高频交流试验原理上与堵转试验相似，电机转差频率较高，转子中电流频率远大于实际运行时的频率，此时转子线圈集肤效应将影响转子电阻的测量精度。一般认为集肤效应对转子电阻辨识的影响是线性的，与转子电流频率有关。可将直接计算到的转子电阻用下式表示:

式中:Rr是辨识的电阻值，Rr0是真实的电阻值，αf表示由集肤效应产生的与频率有关的线性误差。

为补偿该线性误差，克服集肤效应的影响，在单相高频实验过程中，进行两次不同频率的电压激励，两个激励频率都在额定频率附近选取即可。两次试验分别计算得到两个转子电阻Rr1和Rr2。然后通过下式，即可较精确地辨识出电机正常运行时的转子电阻值。

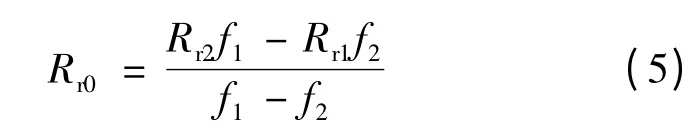
式中:f1和f2分别表示两次实验的激励频率。

2.3 定转子互感参数辨识

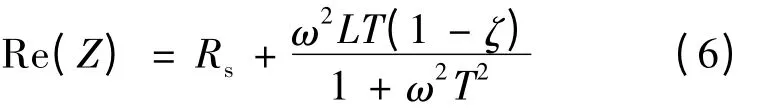
从上式可以看出，互感Lms就包含在L、T、ζ 三个变量中，求得了任意一个变量，即可求得互感Lms。

单相低频交流试验方法的步骤如下:

(1)对单相线圈通低频交流激励，检测输出电压、电流有效值和功率因数，计算负载电抗虚部Im(Z)。即:

(2)将L、T2、ζ 三个变量作为Im(Z)中包含的未知参数，用不同频率的激励电压重复第一步的单相低频交流试验，得到三个不同频率下的Im(Z)，建立三元一次方程组，求解上述三个未知变量;

(3)根据Lms与上述三个变量的关系，求解出定转子互感Lms。

将第二步与第三步的计算合并，得到定转子互感Lms的计算公式:

式中:ω1=2πf1;ω2=2πf2;ω3=2πf3;Z1=Im(Z1);Z2=Im(Z2);Z3=Im(Z3)，下标1、2、3 表示三次三相低频交流试验。

上述方案中有两个问题需要仔细研究:为什么用电抗虚部而不用电抗实部进行计算;如何选取激励信号的频率。下面对此进行详细分析。

第一，使用电抗虚部进行计算的原因主要是为了避免死区时间引起的输出电压参考值误差对辨识精度的影响。图4 对死区时间影响输出电压的原理进行了说明。

图4 上的曲线是三相桥交流输出电流曲线Ireal、给定电压曲线Uref、实际电压曲线Ureal。根据三相桥工作原理，死区时间引起的电压误差与电流极性是相反的，所以Ireal为正时，实际电压小于给定电压;Ireal为负时，实际电压大于给定电压。计算电路电抗时，电抗实部Re(Z)等于电压与电流同相位部分之比，虚部Im(Z)等于电压与电流正交部分之比。将图4 中的交流电压拆分成与电流同相位和正交两部分，如图5 所示。

图4 死区时间对输出电压的影响

图5 中间U1曲线即为输出电压中与电流同相位的部分，粗曲线是实际值，可以看出此时一个周期内参考电压有效值明显大于输出电压有效值;图5最下面的U2曲线是输出电压中与电流正交的部分，可以看出一个周期内参考电压和实际电压有效值是相等的。所以死区时间所引起的电压误差是作用在电抗实部Re(Z)上的。

图5 输出电压相位拆分图

另外，电抗实部的表达式中还含有定子电阻Rs，其测量误差也会影响互感的辨识精度。综上，为了避免死区时间误差和定子测量误差对定转子互感辨识的影响，采用电抗虚部Im(Z)进行计算。

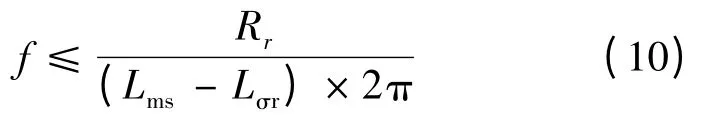
电机参数离线测试之前，Lms是未知量，所以低频激励信号频率的选取需要一定的经验。根据约束条件，设定的频率可以尽量低一些。本文对一系列感应电机进行了仿真计算，并考虑到变频器能够正常输出的最低频率，确定三次单相低频交流测试的频率可以在0.1 ～0.2 Hz 范围内选取。

3 仿真与实验验证

3.1 仿真验证

运用本文提出的电机参数离线辨识方案，在MATLAB 中对各个等级的一系列异步电动机的内部参数进行仿真检测，仿真结果如表1 所示。

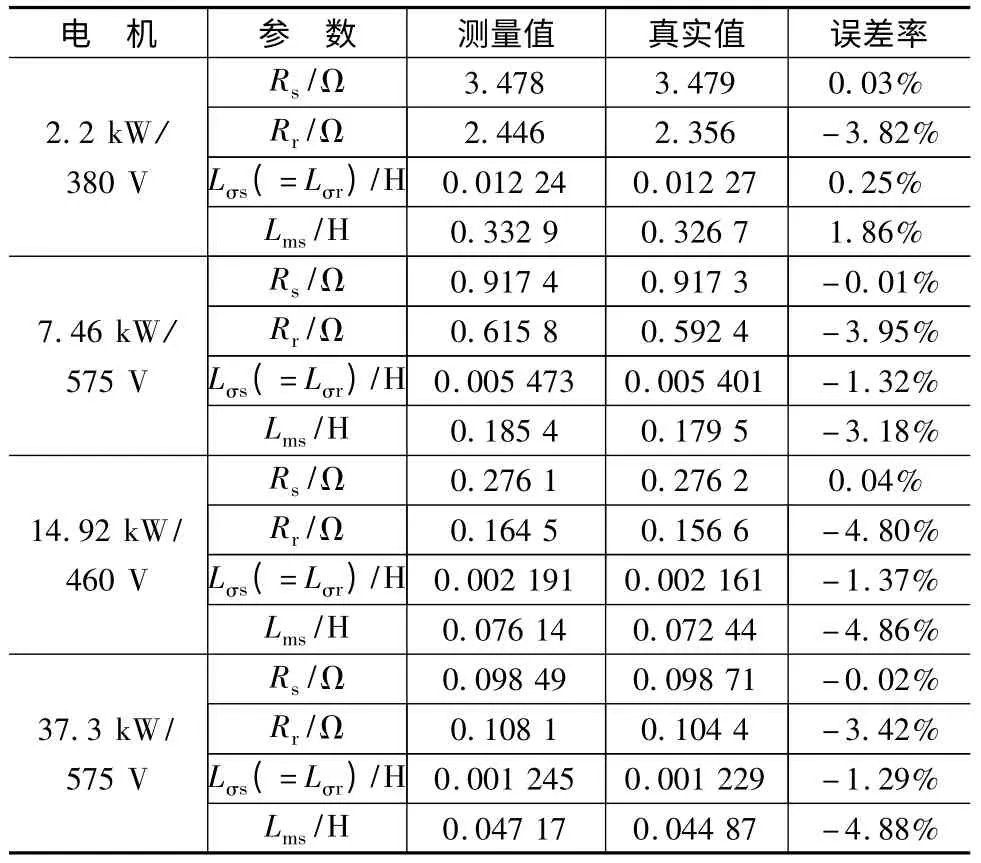
表1 电机参数离线辨识MATLAB 仿真结果

本次试验结果表明，电机参数测量误差都在5%之内，该电机参数离线辨识方法对各个电压等级、各个功率等级的电机都是适用的。

3.2 实测验证

将本文的电机参数离线辨识方法进行程序编写，嵌入到某变频器系统中，对该系统中的电机进行参数辨识。该电机铭牌参数:额定功率2.2 kW，额定电压380 V，额定电流5.2 A，额定频率50 Hz，额定转速1 430 r/min。运用上述直流试验，单相高频交流试验和单相低频交流试验，对电机定子电阻、定子漏感、转子电阻、转子漏感、定转子互感五个参数进行辨识，辨识结果如表2 所示。

表2 2.2 kW/380 V 电机参数离线辨识实测结果

从表2 的试验结果可以看出，虽然实测试验辨识精度比仿真实验稍差，但仍然是较为准确的，其辨识出的参数完全可以用来进行矢量控制。

4 结 语

本文提出一种静态条件下的异步电动机参数离线辨识方法。该方法通过直流试验、单相高频交流试验、单相低频交流试验以及相关补偿措施，精确辨识出电机内部的定子电阻Rs、定子漏感Lσs、转子电阻Rr、转子漏感Lσr和定转子互感Lms五个参数。通过仿真实验和实测试验，证实了该方案的有效性。该方案应用时不会产生电磁转矩，不会受连轴负载的影响，所以不需要对装配好的电机负载进行拆卸，具有较高的使用价值。

［1］ Toliyat H A，Levi E，Raina M. A review of RFO induction motor parameter estimation techniques［J］.IEEE Transactions on Energy Conversion，2003，18(2):271－283.

［2］ Attaianese C，Nardi V，Tomasso G. A self－commissioning algorithm for VSI－fed induction motors［J］. IEEE Transaction on Power Electronics，2002，17(6):1017－1023.

［3］ Grantham C，Mckinnon D J.Rapid Parameter Determination for Induction Motor Analysis and Control［J］. IEEE Transaction on Industry Applications，2003，39(4):1014－1020.

［4］ Gastli A.Identification of induction motor equivalent circuit parameters using the single－phase test［J］.IEEE Transactions on Energy Conversion，1999，14(1):51－56.