PCB铣加工中的简单数学原理

2014-01-13龚磊王嘉

印制电路信息 2014年11期

龚磊王嘉

（天津普林电路股份有限公司，天津 516008）

1 前言

伴随PCB多样化的应用，外观品质和尺寸精度更优的数控铣成为硬板PCB最主要的成型工艺，铣成型的优点显而易见，复杂外形轮廓的铣削、板边平整光滑、尺寸精度高。但在当下PCB产品种类和外形复杂程度不断增加，尺寸误差要求±0.1mm、甚至±0.05mm的情况下要满足客户需求的高精度尺寸并不容易，了解PCB数控铣加工中板尺寸变化的规律和原因是实现精密控制的必要前提。

2 铣削的特点

与冲切、V-cut加工时垂直与板面的受力不同，数控铣下刀后铣削的主要作用力在与板面相同的二元平面内，所以铣加工较少产生PCB板因Z向承力所致的分层、开裂等缺陷，而较多产生板边波纹和尺寸偏差，这些成因与成型机主轴顺时针旋向和铣刀的结构密不可分，图1和图2分别为上排屑鱼尾型通用铣刀的切削刃实图和铣加工时的刃部横切示意图，铣加工时铣刀刃与成型机主轴为相同的顺时针旋向。

图1 铣刀切削刃实图

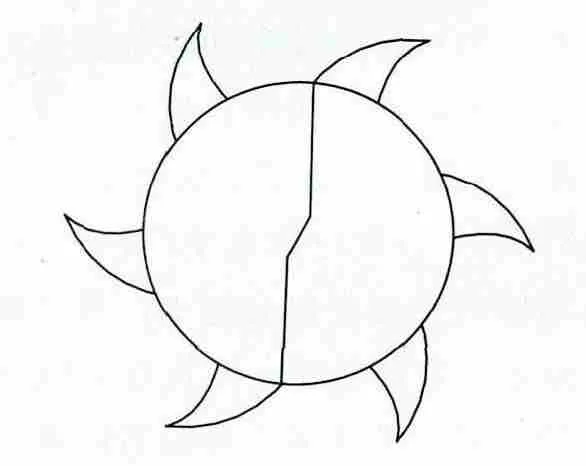
图2 铣刀刃部横切示意图

3 铣刀进给方向与尺寸关系

PCB的铣加工过程铣刀的运动其实可以近似看成顺时针匀速圆周运动与匀速直线运动的合成，如图3，如果忽略铣刀进给方向的直线运动，只考虑主轴自转的圆周运动，则静态观察t1与t2两个时刻，理想状态下两侧残余的基板突尖大小是相同的。

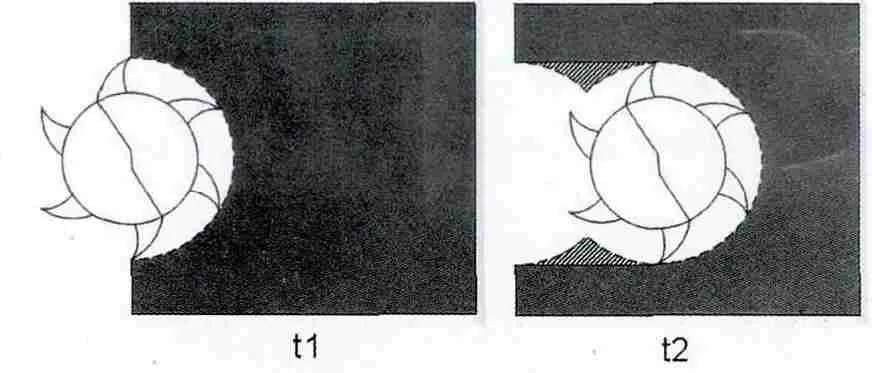
图3 铣刀圆周运动两侧残余基板突尖

实际因为有匀速直线F速度的合成，我们用极限的方法，将铣刀等效为只有一个切削齿，假设一个完整的切削周期为T，截取两个时间段分析，分别为迎着和背向切削刃一侧刀齿刚过最低点后的1/4周期内，如图4，刀齿的切削速度为直线进给速度Fe和圆周切线速度Fs的合速度。

图4 铣刀不同时间段速度分析

由图4可以看出，在迎着切削刃周期内，合速度快，基材边被切削后相对平缓、突尖程度小，而背向切削刃周期内，合速度慢，基材边被切削后相对陡峭、突尖程度大，其运动轨迹可近似看做图5所示的螺旋线，背向铣刀切削方向的一侧基板突尖幅度总是比迎着切削方向一侧的要大。正因如此，铣刀进给方向对板尺寸的影响始终存在于PCB铣板的加工过程，当然不同的机台、排尘和参数选择对进给方向两侧的尺寸偏差影响，幅度会稍有不同。从图中可以看到，理论上每个刀齿的切削周期T越短、也就是主轴转速S提高，直线进给速度F降低，相应的切削后残留的基板突尖程度也会越小，尺寸精度相对越高，但差别是一定存在的。以我公司2.0 mm铣刀为例，常规参数相同条件下，进给方向两侧的尺寸偏差可以达到约0.05 mm左右。

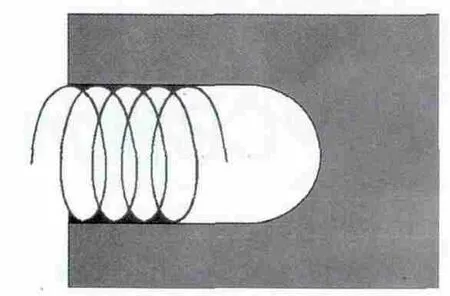
图5 铣刀合成运动轨迹示意

4 圆弧插补与直线尺寸

PCB数控成型机的平面铣切都是通过X和Y方向的坐标轨迹点动来实现的，圆弧铣切的实质既是用多段直线逼近圆弧，利用CNC系统的圆弧插补算法增加直线线段的数量，也就是数据密化来提高生成圆弧的精度。

圆弧插补时，轮廓步长作为内接弦线对圆弧进行逼近，会存在一定的半径误差，如图6，采用弦线（l）逼近时，半径为r的圆弧其最大半径误差为er，对应的圆心角亦即步距角为δ，在进给速度F、插补周期T条件下，半径误差er由上图进行推导如下式（1）。

图6 圆弧内接弦线插补

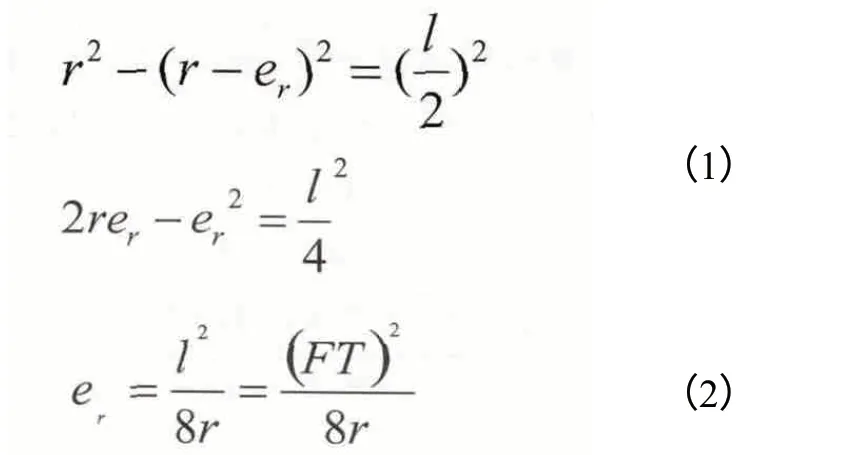
简化表达公式，舍去高阶无穷小量，半径误差er可得出式（2）。

可以看出圆弧插补的半径误差er与插补周期T和进给速度F的平方成正比，这里插补周期由CNC系统决定，进给速度F的降低可以提高圆弧成型的精度，而与实际圆弧的半径r成反比，也就是半径越大的圆弧，误差会相对越小。但整体上，从图6可以看出作为内切圆弧，铣后的内径会较理论值小，作为外切圆弧，铣后的外径亦会较理论值小。

比较典型的情况就是如图7所示的直线与圆弧相连的这种情况，因为存在圆弧插补的误差，即使在相同的条件加工，圆直径D与直线宽度L之间仍存在一定的偏差，以我司产品和加工条件为例，直径约11.0 mm的圆，其加工后尺寸较之直线宽度会小约0.04 mm，这部分偏差就需要在掌握实际情况的基础上，在铣程式中进行相应的补偿，以便于过程加工的尺寸控制。