基于不同需求等级改进的动态频谱分配算法

刘俊彤，王可人，张兴良，冯 辉

（解放军电子工程学院，安徽 合肥 230037）

0 引言

随着无线通信技术的高速发展，人们对无线通信业务需求的不断增加与无线频谱资源匮乏之间的矛盾越来越尖锐。针对频谱资源的不足，认知无线电（Cognitive Radio，CR）［1］网络中的动态频谱分配技术（Dynamic Spectrum Allocation，DSA）能够灵活地使用空闲频谱，实现空闲频谱的再利用，从而提高频谱利用率［2］。在目前的研究中，DSA 技术包含非合作DSA 与合作DSA，非合作DSA 是指非授权用户进行频谱检测，在授权用户不使用的频段进行频谱接入。而合作DSA 则是采用特定的算法对频谱资源进行统一的动态分配［3-4］。

现有文献多对合作DSA 进行分析讨论，文献［5］采用频谱拍卖的方式将主用户的空闲频段分配给次级用户，分别解决了拍卖过程中可能出现的次级用户不诚实报价和共谋的问题，同时还有效地解决了网络效益降低的问题；文献［6］提出了一种基于单频段多赢家拍卖的分配算法，该算法在原始贪婪算法的基础上增加了多重贪婪策略，以较低的计算复杂度获得了较优的解，提高了卖家的收益，有效抑制共谋的发生，同时提高了拍卖的经济收益。文献［7］提出一种以用频冲突等级最小的频谱动态指配数学模型，将频谱指配问题归结为冲突等级评价数学函数的优化问题，该方法能够有效地求解频率指配过程中出现的问题。诸如此类对合作DSA 技术的研究很多，但是，这些研究所建立的系统模型往往不完善，缺乏对业务模型中不同业务需求等级的分析，对不同认知用户接入需求度的差异性考虑较少。

针对上述问题，本文提出一种基于不同业务需求等级的动态频谱分配算法。

1 系统模型与问题描述

1.1 系统模型

在认知无线网络中，合作DSA 由中心控制器来协调和管理CR 用户对空闲频谱的使用，通过收集其控制范围内各CR 用户的频谱感知信息，建立可用频谱数据库，通过多个CR 用户之间相互交换分配信息、协商频谱分配，合力达到全局最优的频谱分配的目的［8］。中心控制器周期性的进行频谱分配，认知用户向中心控制器提供下一个分配周期内所要释放的频谱资源和新需求的频谱资源。系统基本模型如图1所示。

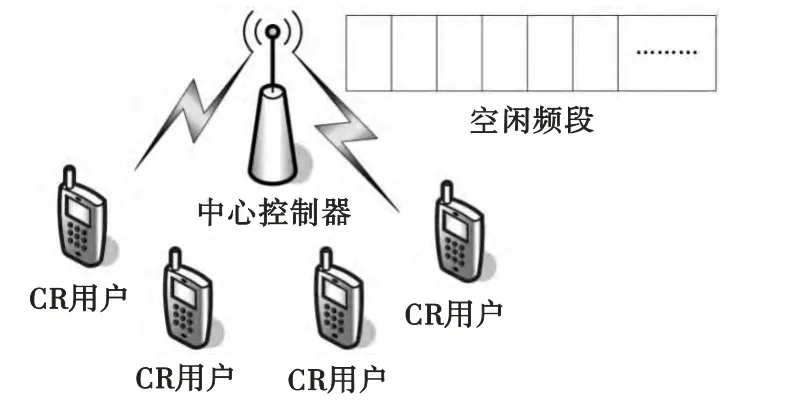
图1 动态频谱分配系统模型Fig.1 The model of DSA system

该模型中，系统的频谱接入机制可描述如下：对于请求接入的CR 用户，中心控制器判断频谱空间中是否存在可供该接入请求使用的空闲频段，若存在，系统对该请求分配一个空闲频段，若不存在，那么该接入请求被阻塞。该模型可以使认知用户按照一定的效用函数共享空闲频谱资源，但没有考虑不同认知用户对频谱接入需求的差异性，为完善DSA系统模型，该文提出一种基于不同业务需求等级的DSA 系统模型。

图2给出了基于业务需求等级的动态频谱分配模型。该模型将认知网络中的CR 用户依据其不同的业务需求等级分为一级用户和二级用户，其中一级用户的接入优先级高于二级用户，二级用户的接入状态对一级用户可视作透明的。

图2 不同业务需求等级DSA 分配模型Fig.2 The model of DSA system with different levels of service demand

在该模型中，系统的频谱接入机制可描述如下：

1）一级接入请求：对于一个一级接入请求，当频谱空间中存在可供该接入请求使用的空闲频段时，系统对该接入请求分配一个空闲信道；若频谱空间中不存可供该接入请求使用的空闲频段，但系统存在某个二级用户接入且该接入频段可供该一级用户接入使用时，那么中心控制器将终止此二级用户的接入，空出频段来提供一级用户的接入；若以上两种情况均不存在，那么该一级接入请求被阻塞。

2）一级接入完成：一级接入需求结束时，中心控制器自动释放其占用的信道。

3）二级接入请求：对于一个二级接入请求，中心控制器首先判断频谱空间中是否存在可供该接入请求使用的空闲频段，若存在，则系统对该接入请求分配一个空闲信道，若不存在，那么该二级接入请求被阻塞。

4）二级接入完成：二级接入需求结束时，中心控制器自动释放其占用的信道。

该模型对请求接入的认知用户采取分级操作，对不同需求等级的认知用户赋予不同的接入优先级，更加合理地使用了空闲频谱资源。

1.2 问题描述

根据分析，认知无线网络中的DSA 问题可以等效为图着色问题。设有P 个认知用户竞争接入Q段不连续的频段，将每个认知用户抽象为一个顶点，将每段可用频段映射为一种颜色，则可将频谱分配问题抽象为图着色问题G= （V，E，L）［9］，其中参数定义如下：

定 义 2： 可 用 信 道 矩 阵 L，L =｛lij|lij∈｛0，1｝｝P×Q，lij=1／0表示CR用户i可以／不可以使用信道j。

定 义 3： 干 扰 关 系 矩 阵 E，E =｛eij|eij∈｛0，1｝｝P×P，eij=1／0表示CR 用户i与CR用户j间有干扰／无干扰。若有干扰，则i与j不能同时占用相同的频段；若无干扰，则i与j 可以占用相同的频段。由于i与j 之间的干扰是相互的，因此矩阵E 为对称矩阵。

定义4：信道分配矩阵A，A=｛aij|aij∈｛0，1｝｝P×Q，aij=1／0表示CR用户i已分配／未分配使用信道j。当满足以下条件时A 是有效的：

定义5：效用函数R，对给定的信道分配矩阵A，认知网络会获得相应的网络效益，该效用的大小用认知接入用户量的多少表示。

以图3为例，顶点1～4分别代表4个不同的认知接入用户，其中1和2为一级用户，3和4为二级用户；顶点间连线表示相连接的认知用户不能同时占用相同的频段，否则将产生干扰；Ⅰ、Ⅱ、Ⅲ分别代表3个不同的主用户，其占用频段分别用a、b、c表示，位于主用户覆盖范围（虚线圈）内的认知用户不能复用主用户占用的频段，主用户覆盖范围外的认知用户可将该主用户占用的频段视为空闲频段。

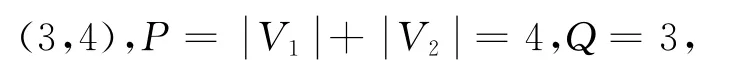
根据分配优先级和最大化用户接入量，可得其中一个有效的信道分配矩阵

图3 问题描述Fig.3 Description of the problem

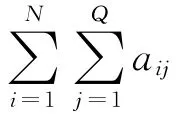
该问题属于NP完全问题，当图较大时，穷举法在呈指数递增的状态空间中寻求最优解会耗费太多的时间和资源。鉴于此，该文在综合考虑频谱资源分配问题的基础上，借鉴自然界生物进化过程中适者生存的竞争机制，选用遗传算法（Genetic Algorithm，GA）解决该问题，并在基本遗传算法的基础上设计了一种基于t分布随机扰动的变异方案，提高了该算法对本模型的整体寻优能力。

遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法［10］。将问题的一个解当作生存环境中的一个个体，以目标函数值或其变化形式来评价个体对环境的适应能力，模拟个体组成群体的进化过程，优胜劣汰，最终获得最好的个体。尽管遗传算法已经广泛应用于处理各类优化问题中，但仍存在诸如收敛速度慢，搜索效率低，容易陷入局部最优等问题。国内外学者做了诸多努力来寻求更好的改进方法，文献［11］提出一种等级变异的选择算法，将变异尺度分成若干等级，提高了免疫算法的寻优性能；文献［12］为提高变异强度，提出了一种基于强化变异算子的遗传算法，在寻优速度和寻优质量上均有较大改进。通过分析比较一些学者提出的改进算法，我们知道，柯西变异的全局探索能力较强，能够有效地保持种群的多样性；而高斯变异的局部开发能力较强，可以保证进化后期的收敛速度。为综合两者的优点，该文提出一种基于t分布变异的遗传算法。

t（n）分布又称学生分布，含有参数自由度n，当n=1时，t（1）服从柯西分布；当n→∞时，t（∞）服从标准高斯分布，一般n取值较大（大于50）时即可认为t分布近似服从标准高斯分布。因此可以通过调节参数n，使算法前期具有良好的全局探索能力，而在进化后期又具备较优的局部开发性能，以此来提高算法的整体寻优能力。

t分布变异遗传算法就是在原有的个体上附加一个服从t分布的随机扰动，即：

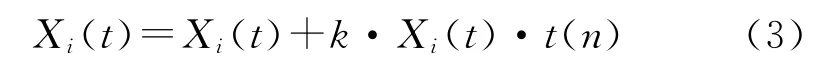
t分布变异首先用历史最优染色体替换当前最差染色体形成中间种群，然后对中间种群的染色体按式（3）变异，并计算当前染色体的目标函数值，而后继续执行GA 基本寻优运算。如此充分利用了当前个体的已知信息进行扰动，增加了种群状态的多样性，有利于算法进行全局搜索，同时也提高了算法的搜索速度。

2 基于t分布变异GA 的认知无线电频谱分配算法

在基于t分布变异GA 的认知无线电频谱分配算法中，每一条染色体编码采用的二进制串表示一种可能的频谱分配结果，染色体中的二进制码为1／0代表该可用频谱已分配／未分配给相应的认知用户。由于可用信道矩阵L 中值为0 的元素位置相对应的信道分配矩阵A 中元素值必为0，故仅对与L 中值为1 元素对应的A 中的元素进行染色体编码，即染色体的个数等于L 中值为1的元素的个数。图4给出了P=4，Q=3时的染色体编码结构示例。

图4中xi= ［1，0，0，1，0，0，1，1］ 为初始种群 中第i个染色体的编码结果，对结果进行适应度评价时需要将其映射为信道分配矩阵A，映射过程可表述为：将染色体编码后的每一位按行逐个填充到与L 中值为1的元素位置相对应的A 的元素。

图4 染色体编码结构示例Fig.4 The example of chromosome coding structure

染色体编码应满足如下约束：对任意空闲频段m（0≤m≤Q），信道分配矩阵A 中的元素应满足aim·ajm·eij=0。由于该分配所要实现的目标是最大化用户接入量，故将R（A）做为适应度函数，随着进化代的进行，适应度函数值应向着增加的趋势改变，当达到最大迭代次数时，算法终止，此时对应的信道分配矩阵A 即为算法最终的分配结果。该分级模型中，首先对N 个一级用户应用该算法对Q 段空闲频段进行分配，继而将剩余的空闲频段应用该算法分配给M 个二级用户。

综上所述，该文提出的基于t分变异GA 算法的频谱分配流程如下：

1）算法初始化，初始化种群规模S，变异概率pm，最大迭代次数U。

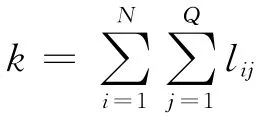
4）交叉产生新个体，保留新个体中经过映射后满足aim·ajm·eij=0条件的个体，并补充新个体至总群规模S。

5）t分布变异操作，变异操作在原有的个体上附加一个服从t分布的随机扰动，Xi（t）=Xi（t）+k×Xi（t）×t（n），并计算当前染色体的目标函数值，而后继续执行GA 基本寻优运算，充分利用了当前个体的已知信息进行扰动。

6）适应度评价，对子代群体进行适应度评价，从父代群体与子代群体中选择适应度最高的个体，替换当前子代群体中的最差个体，并将该最佳个体保存至Bi中。如此，保留了遗传操作过程中的最佳个体。

7）判断是否达到最大迭代次数U，若达到，将Bi中保存的二进制串映射为A 的形式；否则，继续执行遗传算法操作。

3 仿真及性能分析

仿真环境设置：取认知接入用户的个数P =25，其中一级接入用户N =10，二级接入用户M =15，空闲频段个数Q=28，仿真过程中，信道可用矩阵L25×28与干扰关系矩阵E25×25由系统随机生成，系统获得的网络效益以用户接入量衡量，由于考虑不同需求等级的认知用户接入系统会产生不同的网络效益，因此，设一级用户接入系统获得的网络效益值为2，二级用户接入系统获得的网络效益为1。算法采用二进制编码方式，基本参数设置如下：交叉概率为0.6，变异概率为0.001，种群规模为30，最大进化代数为500。在对算法进行t分布变异操作时，取n=1时，变异类型为柯西变异，取n=100时，变异类型为高斯变异，由于高斯变异中期收敛速度较快，柯西变异全局搜索能力强，故对进化代数≤200时采用高斯变异，当进化代数＞200时采用柯西变异。

由图5可见，加入t变异操作后，GA算法的收敛速度和整体寻优能力较普通GA 算法有明显改善，且与穷举法所获得的网络效益并无显著差异，但穷举法的计算复杂度为2q（q 为染色体编码位数），需要耗费过长的运算时间。仿真结果表明了t变异GA算法对处理该问题的有效性和可用性。

为了进一步对比所提出的基于不同需求等级DSA 模型与不考虑需求等级DSA 模型对系统性能产生的差异，图6 给出了20 种不同初始条件下（L25×28与E25×25不同）两种模型经过DSA 算法分配后各自获得的网络效益。

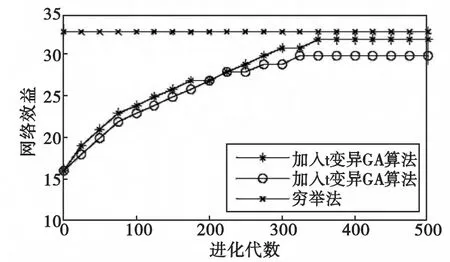
图5 算法性能比较Fig.5 Comparison chart of the algorithms

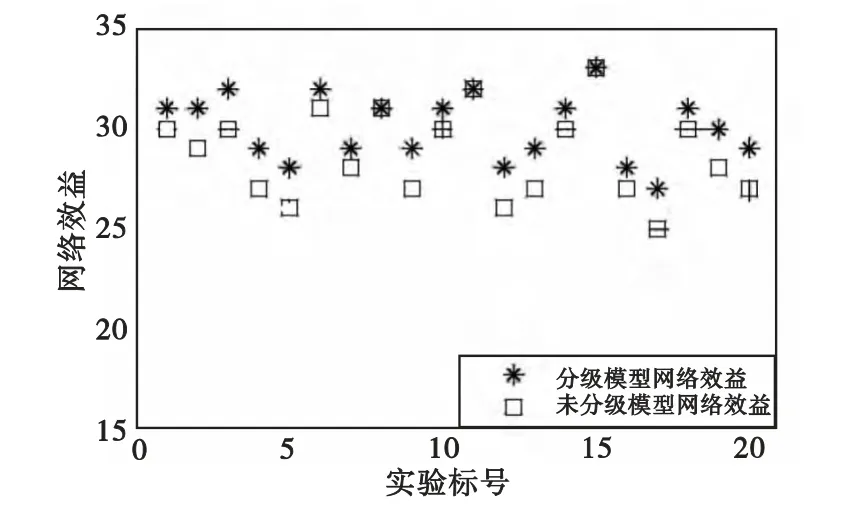
图6 分级模型与未分级模型网络效益比较Fig.6 The comparison chart of the system profits between classification model and common model

由图6可见，不同实验初始条件下，分级模型获得的网络效益均高于未分级模型获得的网络效益，在20次试验中，分级模型获得的平均网络效益为30.05，未分级模型获得的平均网络效益为28.70。仿真结果表明了该分级模型对处理不同需求等级DSA 分配问题的优越性。

图7给出了10种不同初始条件下的DSA 分配结果，在10 次试验中，一级用户的平均接入率为94%，二级用户的平均接入率约为77%，可见分配优先满足了一级用户的接入请求，同时也基本保证了二级用户的接入。表明该DSA 分配方法对处理不同需求等级用户接入的有效性。

图7 频谱分配结果Fig.7 Results of the dynamic spectrum allocation

4 结论

为解决CR 网络中不同业务需求等级频谱分配问题，本文综合考虑接入用户的业务需求等级与系统的网络效益，提出了一种基于不同需求等级改进的动态频谱分配算法。该算法将频谱资源分配建模为0-1整数规划问题，提出了一种基于t分布变异GA的认知无线电频谱分配算法。仿真结果表明：t变异GA 算法对处理该问题具有很高的有效性和可用性；在处理不同需求等级次用户接入问题上，该文提出的分级模型可显著提高系统的网络效益。

本文所提模型假设次用户的接入需求等级不发生变化，对于次用户接入需求等级随条件变化的系统模型有待于进一步研究。

［1］MITOLA J.Cognitive radio architecture evolution［J］.Processings of the IEEE，2009，97（4）：626-641.

［2］NIYATO D，HOSSAIN E，ZHU H.Dynamic spectrum access in IEEE802.22based cognitive wireless networks：agame theoretic model for competitive spectrum bidding and pricing［J］.IEEE Wireless Communications，2009，16（2）：16-23.

［3］MODY A N，SHERMAN M J，MARTINEZ R.Survey of IEEE standards supporting cognitive radio and dynamic spectrum access［C］／／Proceedings of the IEEE MILCOM.San Diego，CA，USA，2008：1-7.

［4］ETSI.Reconfigurable Radio Systems（RRS）；Cognitive Radio System Concept［R］.EU：ETSI TR 102 802 V1.1.1，2010.

［5］ZHOU X，ZHENG H.Breaking bidder collusion in large-scale spectrum auctions［C］／／MobiHoc'10，Proceedings of the Eleventh ACM International Symposium on Mobile Ad Hoc Networking and Computing.Chicago，Illinois，USA：2010.

［6］张文柱，王凌云.基于单频段多赢家拍卖的动态频谱分配［J］.通信学报，2012，33（2）：1-6.

［7］杨奎.一种基于离散粒子群优化的战场动态频谱指配策略［J］.电讯技术，2012，52（5）：755-760.

［8］HAN Z，ZHENG R，POOR H V.Repeated auctions with bayesian nonparametric learning for spectrum access in cognitive radio networks［J］.IEEE Transactions on Wireless Communications，2011，10（3）：890-900.

［9］Wang F，Krunz M，Cui S.Price-based spectrum management in cognitive radio networks［J］.IEEE Journal of Selected Topics in Signal Processing，2009，2（1）：74-87.

［10］Hwang S，He R S.Improving real-parameter genetic algorithm with simulated annealing for engineering problem［J］.Advances in Engineering Software，2006，37：406-418.

［11］宋丹，赖旭芝，吴敏.基于等级变异的克隆选择算法［J］.模式识别与人工智能，2011，24（3）：438-443.

［12］Liu Fei，Zeng Guangzhou.Study genetic algorithm with reinforcement leaning to solve the TSP［J］.Expert Systems with Applications，2009（36）：6995-7001.