传感器安装对电磁转矩测量的影响

高 楷，郭军献，李福松

（1.机电动态控制重点实验室，陕西 西安 710065；2.西安机电信息技术研究所，陕西 西安 710065）

0 引言

采用精确制导组件（Precision Guidance Kit，PGK）进行弹道修正的二维弹道修正引信具有“一维动作，二维修正”的功能，可以使常规弹药获得精确打击能力并降低作战成本，在未来具有很高的使用价值。PGK 控制组件中电机不仅作为发电装置，还作为控制装置使用，其电磁转矩与系统的负载和转速有关，电磁转矩随负载／转速变化特性影响着控制组件的修正能力和控制精度。因此了解控制组件中电机电磁转矩随负载／转速变化特性是实现修正功能及控制精度的先决条件。通过传感器对电机进行电磁转矩测量可得到电磁转矩随负载／转速的动态特性。对控制电机电磁转矩的测量精度应有合适的要求，才能提供可靠的数据给控制端，从而对弹道进行精确的修正。

在对电机电磁转矩进行测量时，需考虑传感器安装角度偏差产生的弯矩对测量精度的影响。目前所查阅到的文献中，对传感器安装时角度偏差引起的误差的研究都只是理论上大致分析了角度偏差对测量精度的影响［1-2］，尚未见分析测量精度与安装偏差角度关系的文章。所以本文提出了电磁转矩测量精度对传感器安装偏差角度要求的计算公式。

1 电磁转矩测量和传感器安装

在对电磁转矩进行测量时，除了传感器安装角度偏差对测量精度产生误差影响外，传感器机械性能引起的误差［3］和传感器应变片贴装位置偏差引起的误差［4］也会对测量精度产生影响，通过选取高规格的传感器可以减弱测量带来的误差影响。

要得到精确的电磁转矩测量数据，在安装传感器时应保证传感器的轴心线与被测系统在同一轴线上。在安装中，如果传感器的安装产生一定的角度偏差，传感器的自身重力会使测试轴上产生弯矩，弯矩在传动轴上产生附加扭矩，使得传感器测量到的转矩值增大，影响电磁转矩的测量精度［5］。为了说明角度偏差引起的误差，以传感器传动轴为对象进行应力分析。根据力学理论在传感器传动轴上取一个正六边形的单元体［6］，如图1所示。其中z 轴为旋转轴，σx为弯矩产生的正应力，τx、τy为电磁转矩产生的剪应力，且τx=τy。

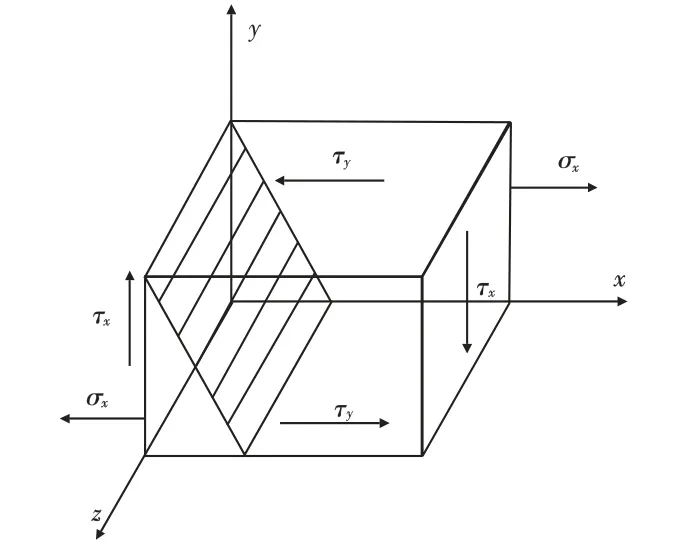
图1 正六边形同时受扭矩与弯矩的应力分析Fig.1 Stress analysis of hexagon by torque and bending moment

在单元体内任意取一斜截面，如图2所示，α 为斜截面外法线与x 轴的夹角。

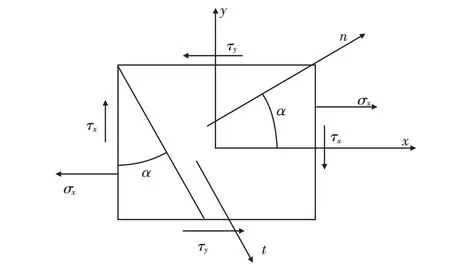
图2 单元体斜截面分解应力分析Fig.2 Section stress analysis of unit cell inclined decomposition

由力学理论［7］可知当传动轴上存在弯矩时，在单元体斜截面上产生的切线应力为转矩与弯矩共同作用的结果：

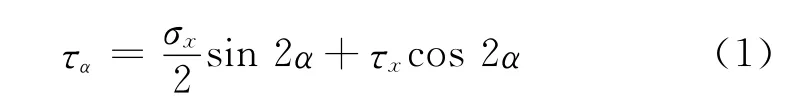
传动轴上，在轴线与轴圆柱面上成135°和45°角的方向上存在最大的且相等的压应力和拉应力［8］。当传感器安装不存在角度偏差（理想情况）时，轴上只存在电磁转矩作用，此时单元体上的剪应力仅由电磁转矩产生，通过应变式传感器的应变片对所受应力的信号传递，可得到电磁转矩；当传感器存在角度偏差时，轴上除了电磁转矩作用外，传感器自身的重力对轴产生弯矩影响，此时单元体上的剪应力由电磁转矩与弯矩共同产生。

2 传感器安装角度计算公式

通过对轴上单元体所受的电磁转矩与弯矩所产生的应力进行分析，分别得出当轴只受电磁转矩和电磁转矩与弯矩同时作用下的应力情况，通过公式的推导，最终得出传感器安装角度偏差时偏差角度与测量精度的关系式。

当传动轴只受电磁转矩的情况时，转矩产生的剪应力：

由式（1）可以得到当α=45°时转矩与弯矩共同作用下的剪应力为：

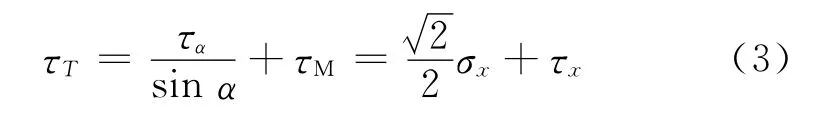
式中：τx=M／wp，wp为轴截面极距，M 为传动轴所受电磁转矩（N·m），σx= Mny／μWz，Mn=mgLsinθ为传动轴所受弯矩（N·m），m 为传感器质量，L 为传动轴长度，y 为单元体到中性轴的垂直距离（m），μ 为被测轴的泊松比，Wz为抗弯截面系数。

当弯矩与转矩共同作用时，测量到的转矩为：

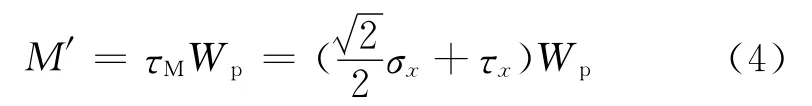
由此可得传感器安装角度偏差引起的转矩误差为：

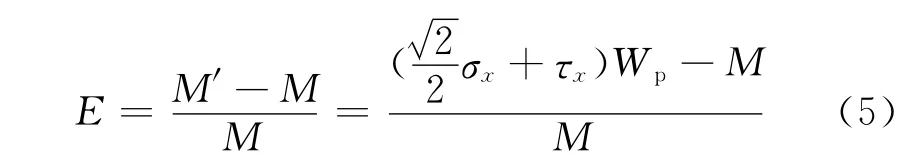
测量系统对电磁转矩的测量误差要求为E ≤q%（6），将参数τx，σx，Wp，M 代入式（6）可得：

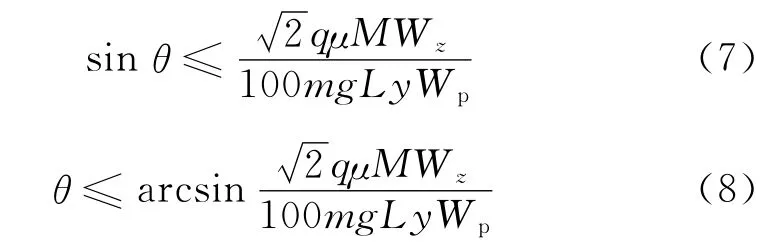
由式（7）可知，当传感器安装偏差角度为（8）时，可以满足安装角度偏差下的测量精度要求。

3 传感器安装角度偏差理论计算与仿真验证

为了验证上述理论分析的正确性，对所研究的电磁转矩测试系统进行了理论计算，同时利用ANSYS软件进行了数值仿真。

假设被测系统的参数如下：传感器质量M=0.5kg，泊松比为0.3，传动轴轴长为20 mm，单元体与中性轴的垂直距离为15mm，电机产生的电磁转矩的变化范围为（5 ～30N·mm）。根据公式（7）可知，较大的电磁转矩所引起的偏差角度也相对较大，因此，角度偏差应小于最小电磁转矩所对应的的安装偏差角度。

通过分析对10种测量精度进行了计算与仿真的验证，其中100%为无误差情况。利用ANSYS仿真软件对传感器传动轴进行了建模，对传动轴进行了10种情况下的转轴所受应力仿真，得到了10种情况下传动轴的应力状态，将数据代入式（6）中得到不同测量精度下偏差角度的仿真结果，图3-6为其中的4种情况。

图3 测量精度为100%Fig.3 Measurement accuracy of 100%

图4 测量精度为99%Fig.4 Measurement accuracy of 99%

图5 测量精度为98.5%Fig.5 Measurement accuracy of 98.5%

图6 测量精度为98%Fig.6 Measurement accuracy of 98%

当无角度偏差时，传动轴上所受应力为τ初；当存在角度偏差时，传动轴上所受应力为τ偏。将100%测量精度情况下的应力与其他测量精度情况下的应力代入式（5）进行计算，得到不同测量精度下偏差角度的理论计算结果，其中精度为ξ=1-E。表1为10种情况下测量精度的仿真结果与理论计算结果。

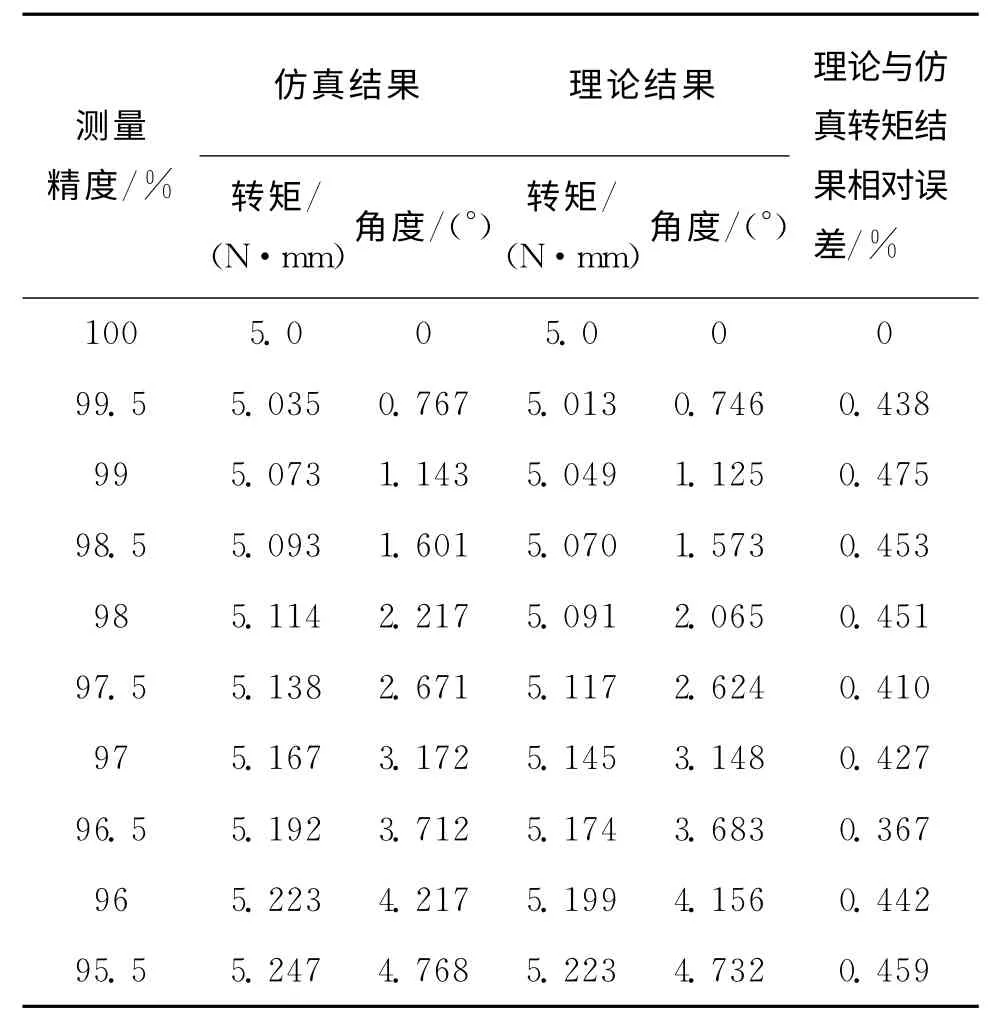
表1 10种情况下测量精度的仿真结果与理论计算结果Tab.1 10Cases measurement precision of simulation results with the theoretical calculation results

由表1可得安装偏差角度与测量精度的关系，如图7所示。偏差角度越大，产生的误差越大，偏差角度与测量精度在一定精度范围内近似为线性关系，由表可知理论计算结果与仿真结果基本一致。

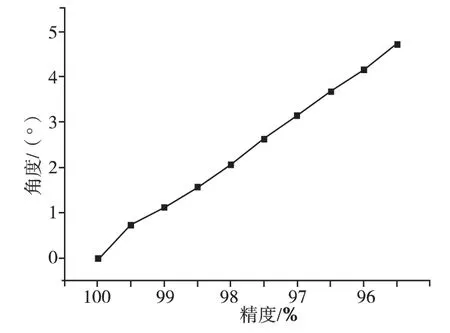
图7 安装偏差角度与测量精度的关系Fig.7 Relationship between installation deviation angle and measurement accuracy

4 结论

本文提出了电磁转矩测量精度对传感器安装偏差角度要求的计算公式。该公式中与角度有关的因素有电机电磁转矩，测量精度和传动轴自身的几何特性，其中角度与电机产生的电磁转矩与测量精度成正比，与传动轴自身的几何特性成反比。通过ANSYS软件对10种情况进行的仿真与理论结果比较，表明理论计算结果与仿真结果基本一致，测量精度与安装偏差角度在一定精度范围内近似为线性关系。利用该公式可得出不同精度要求下的安装偏差角度要求，得到安装偏差角度与测量精度的关系，为电磁转矩测量中传感器安装偏差控制提供参考。接下来将利用测量系统进行试验测量，为理论分析提供进一步的数据验证。

［1］马龙龙.应变式传动轴功率测试系统设计与研究［D］.太原：中北大学，2011.

［2］张晓强.应变式高准确度动态扭矩测量仪的研制［D］.哈尔滨：哈尔滨理工大学，2003.

［3］禹精达，朱晖.传动轴扭矩误差测量分析［J］.机械研究与应用，2011（04）：4-5.

［4］高晓丁，胥光申，王锦.电阻应变片贴装方位偏差对测量结果的影响［J］.西安石油学院学报，2001（16）：41-43.

［5］赵思宏，范惠林.电机转矩转速测量方法的分析［J］.光学精密工程，2002（10）：290-294.

［6］孙望超，李冬华.工程力学［M］.北京：科学技术出版社，1994.

［7］张新占.材料力学［M］.西安：西北工业大学出版社，2006.

［8］张有颐.转矩测量技术［M］.北京：计量出版社，1996.