基于分水岭和形态学的图像特征提取方法

韦 皞，张光锋，娄国伟

（南京理工大学电子工程与光电技术学院，江苏 南京 210094）

0 引言

由于毫米波辐被动成像能够穿透一定厚度的非金属介质来探测隐蔽目标，可以进行全天时全天候工作，其在公共安全检查领域具有十分广阔的前景［1］。为了提高成像的质量和分辨率，目前的研究方向主要集中在提高辐射计空间分辨率的硬件方法和对毫米波辐射图像进行图像处理的软件方法上［2］。使用干涉成像原理的合成孔径技术可以提高空间分辨率，但是其结构与算法复杂、成本造价较高，所以基于图像处理技术的软件方法较为实用和经济。

现有的图像特征提取算法中常用的有基于边缘分割的微分算子，但这些算子都属于高通线性滤波器，不适用于高频范围的噪声和边缘，故对目标边缘模糊、毛刺噪声较多、边界过渡带混叠的毫米波图像边缘检测效果并不理想［3］。因此，结合分水岭算法和形态学，文中根据目标的毫米波辐射特性提出了一种毫米波辐射图像的特征提取算法。

1 研究基础

毫米波辐射计进行成像工作时，会受到接收机部件因素、数据采集、周围环境温度和天气等因素的影响，获得的图像具有较差分辨率，会出现目标边缘模糊、毛刺噪声较多、边界过渡带混叠。可以使用以下一些方法原理对图像质量进行提高。

1.1 数学形态学

数学形态学是建立在几何结构基础上的一种思想，近年来也开始应用在了图像处理和模式识别等领域。数学形态学使用结构元素来测量和提取待处理图像中的相应形状［4］。

形态学运算的基础是：膨胀和腐蚀。设待处理的原 始 灰 度 图 像 为I （x ，y） ，所 使 用 的 结 构 元 素为SE （x ，y） 。

膨胀定义为：

形态学膨胀运算其实是指在图像的边缘处理中为对象增加像素。经过膨胀处理后的图像在灰度级上要比原始图像更亮，所以我们可以用它来增强亮区域的边缘，消除图像中的暗细节。

腐蚀定义为：

形态学腐蚀运算其实是指在图像的边缘处理中删除对象。经过腐蚀处理后的图像，与膨胀运算的结果相反，在灰度级上要比原始图像更暗。同理，我们可以用它来增强暗区域的边缘。

形态学中的开运算与闭运算定义如下：

开运算：

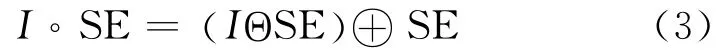
闭运算：

开运算能够保持整体图像灰度级相对不变，消除比结构元素小的亮区域，保留大的亮区域。而闭运算能够削弱暗特征，同时不影响亮区域和背景。所以常使用开和闭运算进行图像预处理。

高帽（Top-hat）运算是通过I x，（ ）y 减去其开运算，而低帽（Bottom-hat）运算是通过图像的闭运算减去I （x ，y） 。它们分别表示为：

对于暗背景图像上的亮区域，一般采用高帽运算进行处理，因为它可以去除复杂的背景并保留图像中灰度值高的部分；而对于亮背景图像上的暗区域，一般采用低帽运算进行处理，因为它可以增强物体之间的间隙并保留图像中灰度值低的部分。原图像通过加上Top-Hat 运算再减去Bottom-Hat运算，图像可以得到增强。

1.2 边缘检测算子

边缘检测算子是基于边缘的分割算法，它检查每个像素的领域，在幅度和方向上对其灰度变化率进行量化。在图像处理的研究中，边缘检测算子是非常活跃的课题领域。常用的边缘检测一阶和二阶微分算子有：Robert算子、Sobel算子、Prewitt算子、LOG 算子、Canny算子。

1.3 分水岭算法

分水岭算法的基本思想是把一副待分割图像看作海拔不同的地形图，图中各像素灰度值对应地形图中该点的海拔高度［5］。

假设一待分割灰度图g （x ，y） 有h 个极小区域，分别用K1，K2，…，Kh表示这些区域，用F K（ ）i 表示极小区域值为Ki的区域。设有n次浸没过程，第n次浸没时的灰度值相应为n。水位从n=min+1到n=max+1变化，其中min和max分别为图像的最小和最大灰度。用M［n］表示满足g （x ，y） ＜n的所有点的集合，则可定义第n次浸没过程与Ki相关的像素集合为Fn（Ki），它可表示为：

定义第n 次被水浸没的集水区域，其并集为F［n］，表示为：

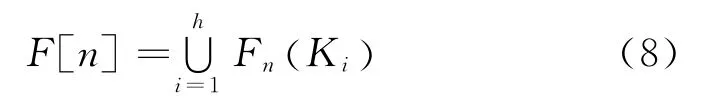
令F［min+1］=M［min+1］，通过递归用F［n-1］计算F［n］。假设M［n］的每个连通分量p ∈P［n］，存在三种情况：

1）p ∩F［n-1］的结果为空；

2）p ∩F［n-1］的结果非空，包含F［n-1］中的一个连通分量；

3）p ∩F［n-1］的结果非空，包含F［n-1］中的两个或两个以上连通分量。

第1）种情况没有交集，说明此次浸没产生了一个新的集水区域。第2）种情况说明p位于F［n-1］中的某个集水区域内。第3）种情况说明继续浸没时，这些集水区域中的水会融合，所以为了防止不同集水区域之间的水溢出必须在p中修建一个到多个水坝，直到达到水位的最高点。这时水坝边界即对应着图像的分水岭线。

2 基于形态学和分水岭的算法

2.1 形态滤波去噪

图像的噪声一般为高亮区域或者暗区域，通过结合开运算和闭运算进行形态学滤波可以有效地对图像进行滤波降噪。根据图像的具体结构特征来选择开运算和闭运算的组合方式，可以使复合形态学滤波算法的效果最佳。本文先采用2×2结构元素去噪，然后再用3×3结构元素去噪，最后再用5×5结构元素进行去噪。如图1所示，各结构元素代表图像在各方向上的特点。

图1 三种尺寸的结构元素Fig.1 Three structure elements

设计的复合形态学滤波结构如图2所示。

首先用2种2×2的结构元素对原始图像进行运算，不同的结构元素对图像的效果不一样，文中设计一种自适应选择结构元素的方法。各结构元素所占的权重为：

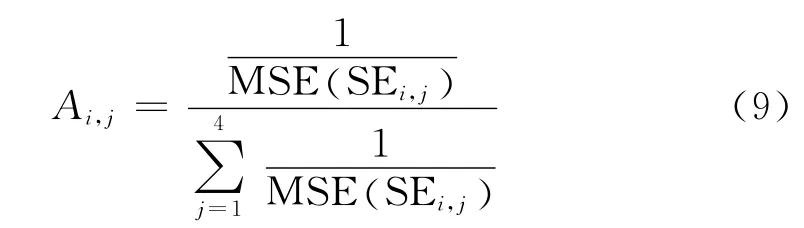
在对结构元素进行加权运算后得到M1，再用4种3×3的结构元素对M1做同样运算得到M2，同理再用8种5×5的结构元素对M2运算得到M。式（9）中为均方误差：

式（10）中，a、b分别为所处理图像矩阵的行和列，E （x ，y） 为 降 噪 后 图 像 的 灰 度 矩 阵 的 元 素，I （x ，y） 为原始图像的灰度矩阵元素。

图2 复合形态学滤波器结构Fig.2 Complex Morphological Filter Structure

2.2 基于分水岭的图像特征提取

1）直方图阈值分割。由于存在大量噪声，原始图像中隐匿物品的边缘部分被严重加宽，所以为了减少边缘模糊，在进行形态学滤波前要先对原始图像进行阈值处理。通过观察原始图像的灰度直方图，选择T=152对其进行阈值分割。阈值分割后的图像即可进行形态学滤波。

2）形态学图像增强对于经过形态学滤波后的图像，为了更好地区分目标与背景，需要进一步对图像进行增强。通过高帽（Top-hat）运算与低帽（Bottom-hat）运算结合的方法进行形态学增强，图像的对比度得到提高，使得进行图像分割后的分水岭线更加准确。

3）形态学梯度处理。采用大小为2的圆盘结构元素，求得预处理图像的形态梯度图像，使得图像中物体边界处出现高亮度像素，而物体内部相对较低，从而为分水岭线的定位制造了有利条件。形态学梯度运算会产生额外噪声，通过高斯滤波器对所得图像进行平滑处理，可以有效消除局部噪声和毛刺。

4）分水岭特征提取。分水岭运算选择待处理图像中的极小值点作为浸没操作的起点，所以在运算前要进行预处理，以避免过度分割。首先提取前景图像，可以通过对增强图像的灰度级取反再进行形态学重构得到。然后再对前景图像进行处理得到局部极大值图像和背景图像。接着对梯度图像进行极小值标定来确定浸没操作的起点。最后对确定了起点的图像进行分水岭运算。

3 实验验证

图3所示为原始实验图像，其中图3（a）为藏匿金属圆盘的行李箱，图3（b）为怀抱行李箱的人，图3（c）为原始伪彩色毫米波辐射图像。从中可以大致看出人体和圆盘的轮廓，但边缘比较模糊，需要进一步进行处理，从而提取出有用的特征。

图3 原始实验图像Fig.3 The original experimental images

图4所示为前期的预处理图像，其中图4（a）为直接转换成的原始灰度图像，图4（b）为阈值分割后进行形态学滤波去噪得到的图像，图4（c）为形态学增强图像。与图4（a）对比可以明显看出图像质量有明显提高，尤其是图像的边缘信息得到了很大的保护。图4（d）为形态学梯度滤波后图像，图4（e）为前景图像，图4（f）为预处理图像。

图5为分水岭边缘提取所得图像及与其他一些微分算子边缘检测方法的对比，其中图5（a）为canny算子，图5（b）为log算子，图5（c）为prewitt算子，图5（d）为sobel算子，图5（e）为分水岭边缘提取图像。图5（f）为分水岭彩色分割图像，可以清晰看到所需检测金属圆盘和人体轮廓特征。可以看出分水岭算法的处理效果优于其他几种微分算子。由于成像过程中受到各种噪声的干扰，原始的毫米波辐射图像质量较差。采用形态学降噪和增强后，有效去除了图像中的噪声并在很大程度上保护了图像的原始信息。通过分水岭算法进行分割得到的图像可清楚看到人体和金属圆盘的轮廓。前期的预处理工作有效避免了图像的过分割，提高了结果的准确性。

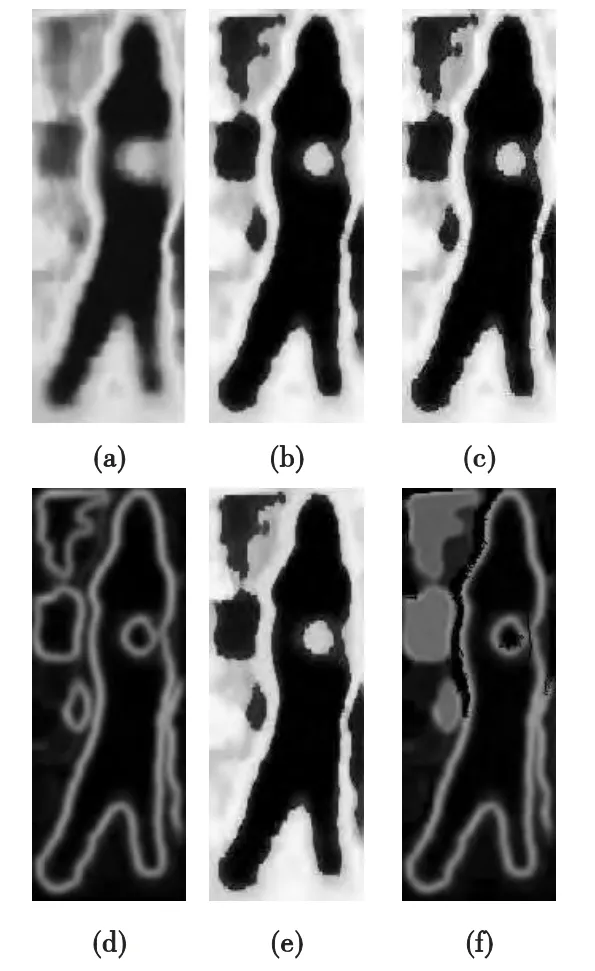
图4 实验预处理图像Fig.4 Pre-processed Experimental Images

图5 分水岭边缘提取和微分算子对比Fig.5 Different results based on watershed and differential operators

4 结论

本文提出了基于分水岭和形态学的毫米波辐射图像特征提取方法。该方法通过自适应的形态学复合滤波方法对毫米波辐射图像进行降噪处理，并对滤波后的图像使用分水岭算法进行图像分割，是对毫米波辐射图像进行特征提取分析的初步尝试。试验表明，该方法可以有效提高图像的质量，清晰反映出金属目标的轮廓，在安检领域必将具有很好的应用前景。但该方法对于一些亮温差值较小区域的分割效果较差，后续研究可考虑结合局部分割的方法［5］对隐匿物品的特征做深入的分析与研究。

［1］Gomez-Maqueda I，Almorox-Gonzalez P，Callejero-Andres C，et al.A millimeter-wave imager using an illumi-nating source［Application Notes］［J］.IEEE Microwave Magazine，2013，14（4）：132-138.

［2］王本庆，李兴国.被动毫米波图像恢复的偏微分方程方法［J］.探测与控制学报，2009，31（5）：25-28.

［3］赵凌，张祖荫，郭伟.基于数学形态学的毫米波图像边缘检测方法［J］.国土资源遥感，2006（4）：19-22.

［4］Levner I，Hong Zhang.Classification-driven watershed segmentation［J］.IEEE Transactions on Image Processing，2007，16（5）：1437-1445.

［5］Cousty J，Bertrand G，Najman L，et al.Watershed cuts：Minimum spanning forests and the drop of water principle［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2009，31（8）：1362-1374.