横向刚度对斜腿刚构桥线性稳定性的影响
2014-01-12梁学锋
梁学锋
(山西路桥第二工程有限公司,山西 临汾 041051)
0 引言
结构的线弹性稳定性计算理论与非线性稳定性分析理论相比,虽然不能得到更为准确的失稳临界荷载,但该计算理论简单明确,在数值计算上作为矩阵特征值分析也能够得到容易处理,其求得的屈曲荷载可作为稳定性分析结果的上限值[1]。此外,该计算方法能够得到明确的屈曲模态,以帮助设计人员把握结构特征。因此,线弹性稳定性计算理论在现阶段仍占有重要地位。
斜腿刚构桥的斜腿在自重或活载作用下处于压弯状态,与常规的桩柱式下部结构相比,斜腿桥墩更容易出现压弯失稳[2-3],从而影响结构的整体稳定性。等截面斜腿刚构桥的稳定性研究已获得较大进展,目前的研究主要侧重于结构尺寸参数及非线性因素对稳定性的影响,而支座约束形式对结构稳定性的影响方面研究较少。本文以结构的线弹性稳定性计算理论为基础,分析不同支座侧向约束形式下斜腿刚构桥的稳定性特征。通过数值模拟计算不同侧向刚度约束下结构的屈曲荷载变化情况,并讨论斜腿横向倾斜角度对稳定性的影响。
1 计算模型及参数设定
本文以某斜腿刚构桥为基础进行稳定性分析。该桥为跨线乡道桥,桥梁全长36 m,跨径组合为12 m+20 m+12 m,斜腿上部与主梁刚接,下部与底座铰接;支座与铰的垂直高度为10 m,如图1所示。主梁为混凝土箱梁结构,其尺寸如图2所示;斜腿采用混凝土双肢矩形截面,横向中心间距为2.75 m,单肢尺寸为0.35 m×0.75 m;斜腿中部设置一道横系梁,其尺寸为0.35 m×0.35 m的矩形截面。

图2 主梁截面图(单位:m)
以下计算均采用Sap2000有限元软件进行,全桥模型概况见图3。根据文献[4],对主梁施加1 kN/m均布荷载,并以该荷载工况为基准荷载分析结构的稳定性特征,计算所得的荷载因子乘以基准荷载就能得到结构屈曲临界荷载。用有限元法计算结构线性稳定性的方法可参考相关文献[5],在此不再赘述。

图3 全桥模型概况
2 不同约束形式下斜腿刚构桥稳定性特征
在一般的设计计算中,桥梁在墩台处支座约束可简化为各种铰接模型。对于有特殊设计的桥梁,此约束可在该基础上增加或减少某个方向的自由度以达到更准确的计算结果。本节计算分析三向约束支座和双向约束支座对结构稳定的影响。三向约束为U1、U2、U3方向刚性约束;双向约束为 U1、U3方向刚性约束;其中U1为纵桥向,U2为横桥向,U3为竖桥向。其余转动自由度均释放。
计算结果显示,三向约束模型的一阶屈曲荷载为548 kN/m;双向约束模型的一阶屈曲荷载为168 kN/m,两者相差3倍以上,三向约束模型的计算结果远大于双向约束模型。因此,在支座处设置U2向刚性约束能有效地增加结构的稳定性。图4和图5显示了不同约束形式的屈曲模态。从中可看出,三向约束模型的失稳形式为桥墩横向挠曲,其具体表现为桥墩局部失稳;而双向约束模型的失稳形式为结构整体横向失稳。

图4 三向约束模型1阶失稳模态

图5 双向约束模型1阶失稳模态
3 支座横向刚度对斜腿刚构桥稳定性的影响
通过以上分析可知,支座的横向约束形式能够明显地影响结构稳定性特征。事实上,桥台处的U2向约束不可能为完全刚性或完全为0,桥梁的横向约束通过支座的横向刚度施加,该值可通过相关参数计算求得。本桥的每侧桥台均设置两个150 mm×150 mm板式橡胶支座,其最大承压能力为196 kN,根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》[6]和《公路桥梁板式橡胶支座》[7]相关公式,并联系实际情况计算得出U2向设计约束刚度为45 kN/m。为表现不同U2刚度对结构的影响,以下将U2向约束刚度分别设置为25.5 kN/m、45 kN/m、67.5 kN/m、90 kN/m、112.5 kN/m,分别计算结构的稳定性特征。本计算中通过侧向弹簧的设置对主梁进行约束,计算结果显示,屈曲荷载随U2向刚度的增加而增加;如图6所示,两者基本呈线性关系。其最小值为176 kN/m,大于双向约束模型的计算结果。
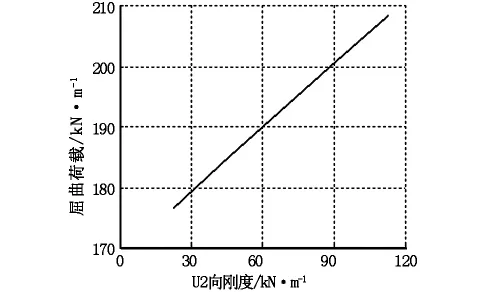
图6 屈曲荷载—U2向刚度关系曲线1
以上计算虽然设置了侧向约束,但其屈曲荷载仍小于三向约束支座模型的计算结果。现将U2向刚度设置为一系列较大值,以分析U2向约束逐渐趋于刚性状态下结构的稳定性特征。图7显示了较大侧向刚度约束条件下结构的屈曲荷载—U2向刚度关系曲线,结构的屈曲荷载随U2向刚度的增加而增加。当刚度大于某一数值时,单位刚度变化引起的屈曲荷载变化量逐渐减小,两者呈现非线性关系;随着U2向刚度的进一步增加,屈曲荷载逼近于三向约束模型的计算结果。三向约束模型的是斜腿刚构桥计算的上限值,而双向约束模型的计算结果为下限值,两者之间有较大差异。实际工程中,桥台处的U2向刚度介于0和无穷大之间,也不会约束刚度为0,因此,准确把握U2向刚度对计算斜腿刚构桥的屈曲荷载尤为重要。
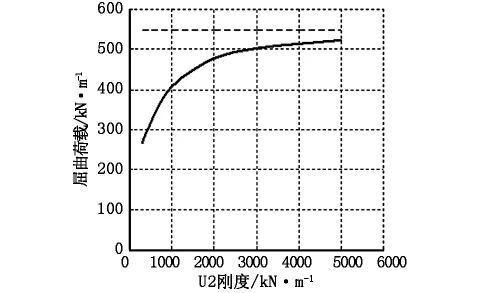
图7 屈曲荷载—U2向刚度关系曲线2
4 桥墩横向倾斜角度对斜腿刚构桥稳定性的影响
为保证斜腿刚构桥的稳定性,通常将斜腿横向设计为一定倾斜角度β[8],如图8所示。该方法可在不用过多地增加造价的前提下有效地增加结构的横向刚度。以下通过计算分析桥墩横向倾斜角度对斜腿刚构桥稳定性的影响,按桥台支座的约束形式不同分别建立两种模型:a)U2 向刚性约束;b)U2 向弹性约束,K=45 kN/m。夹角β分别取为0°、2.86°、4.29°、5.71°和7.13°。计算结果见图9和图10。

图8 斜腿横向倾角示意图

图9 U2向弹性约束模型屈曲荷载计算结果
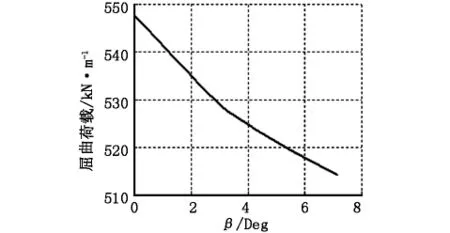
图10 U2向刚性约束模型屈曲荷载计算结果
图9显示了U2向弹性约束模型的屈曲荷载—β关系曲线。随着β的增加,屈曲荷载明显增加,其最大值为最小值的1.5倍。图10显示了U2向刚性约束的模型计算结果,屈曲荷载随β的增加而略有减小,变化幅度在5%以内。因此,桥台支座约束形式对不同的β角模型计算结果有较大影响。实际工程中桥台约束处的U2向刚度不会为无限大,因此,一般情况下可认为斜腿刚构桥的屈曲荷载随β的增加而增加;但对于桥台U2向约束作刚性约束处理的特殊情况,仍需要进行详细分析计算得出合理的结构设计。
5 结语
本文针对通过对斜腿刚构桥U2向约束进行了大量的数值模拟分析。总体上看,增加桥梁横向刚度有利于保证结构的稳定性。以下得出几点结论可供设计人员参考:
a)桥台支座的U2向约束对结构稳定性的影响较大,U2向刚性约束的屈曲荷载远大于U2向无约束的计算结果,因此在稳定性验算过程中,将U2向约束考虑为刚性是不安全的。
b)桥台支座的U2向弹性刚度有利于斜腿刚构桥的稳定性,当刚度较小时,屈曲荷载与刚度呈线性关系;当刚度较大时,屈曲荷载与刚度呈非线性关系;随着刚度的继续增加,屈曲荷载最终逼近于支座三向约束模型的计算结果。
c)桥墩的横向倾斜角度能够增加U2向弹性约束的斜腿刚构桥的屈曲荷载;对于U2向刚性约束的桥梁,倾斜角度的增加一定程度上削弱了结构的稳定性,但屈曲荷载的变化较小。建议对于U2向约束刚度较大的斜腿刚构桥,桥墩的横向倾斜角度可取较小值。
