基于土拱效应的抗滑桩间距计算方法综述

马飞，郭长春

（1重庆市地质灾害防治中心，重庆 401311；2重庆建工第三建设有限责任公司，重庆 400011）

0 引言

抗滑桩通常用于稳定边坡和治理滑坡[1-2]，是将桩插入滑动面（带）以下的稳定地层中，利用稳定地层岩土的锚固作用以平衡滑坡推力，稳定滑坡的一种结构物[3]。由于坡体的横向位移大于抗滑桩的横向位移，使桩迎坡面一侧土体相互挤压，土体抗剪能力得到发挥从而形成了土拱效应，如图1所示。抗滑桩的设计理念是采用非连续结构，利用土体自身强度形成的拱效应将桩间土体的下滑推力传递到桩身来达到支挡的目的[4]。合适的抗滑桩间距是产生土拱效应的前提，而只有产生土拱，抗滑效果才比较明显[5]。而实际桩间距计算中，通常通过单桩承载力或是经验进行估计，不仅结果偏于保守，而且造成了不必要的浪费，因此合理桩间距的确定具有重要的实践意义。

图1 桩间土拱效应示意简图

1 基于土拱效应的计算方法

由于对土拱作用机理、破坏机制和强度条件等认识的不同，对土拱的计算方法也是各不相同，总体来说分为三种类型：（1）通过土拱静力平衡条件得到最大桩间距的计算方法；（2）运用大小主应力理论建立的桩间距的计算方法；（3）以土拱强度为约束条件建立的计算方法。

1.1 静力平衡法

静力平衡法是由土拱受力保持静力平衡，得到静力平衡式，进而推算出桩间距的方法，主要以桩侧摩阻力与滑坡推力间的静力平衡条件进行控制。王世川[6]认为应在桩间距上限值解法的基础上考虑土拱效应的影响，同时也应注意桩断面间土体摩阻力和粘着力的阻滑作用。文献6以土拱效应为基本条件，桩间滑坡推力小于土体与桩侧间的摩阻力，得到下限解的计算式：

式中，R为微元体上的平均压应力，S为抗滑桩的中心距（m）；ψ为土拱影响系数；δ为桩与桩周岩土间的摩擦角（°）；D为桩的长边长度（m）；h为滑体厚度（m）；λ为微元体水平应力与垂直应力之比。其余为土的物理力学参数。

过大的滑坡推力与土拱内部较低的土颗粒抗剪强度耦合作用会造成土拱破坏[7]。王成华假设桩间全部滑坡推力通过桩侧摩阻力承担，得到最大桩间净距计算公式：

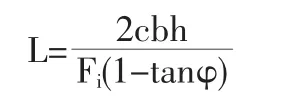
式中，c为沿滑动面滑动土体的内聚力（kPa）；b为抗滑桩侧滑动面以上宽（m）；h为抗滑桩侧滑动面以上高（m）；Fi为单宽滑坡推力（kN/m）；φ为土拱土体的内摩擦角（°）。

冯君在王成华法的基础上认为滑坡推力不仅通过桩侧摩阻力承担，而且土拱自身的剩余抗滑力与拱前岩土体也同时参与阻滑，通过引入隧道工程的普氏系数得到最大桩间净距的计算公式[8]：

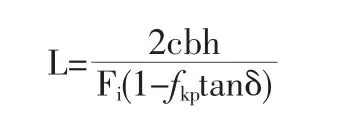
式中，Fi为竖向均布荷载（kN/m）；fkp为普氏岩土体坚固性系数；δ为桩与桩周岩土间的摩擦角（°）；b为土拱沿滑动方向的厚度（m）；c为土体粘聚力（kPa）；h为滑体厚度（m）。

以上理论均从土拱的静力平衡条件着手，考虑了桩侧摩阻力影响，但在滑坡推力的承担问题上相异。单一以桩侧摩阻力承担滑坡推力会使计算偏于保守，而桩前土体的阻滑作用并不明显，提供抗滑力显然不太合理，所以明确阻滑条件是应该值得注意的问题。

1.2 大小主应力法

颗粒体系受纵向力作用，会发生应力偏转而倾于横向分布，从而形成以主应力迹线为拱轴线、约束处为拱脚的拱[9]。而在相邻护壁桩之间会形成大主应力拱[10]，且应力值为常量[11]。大主应力拱支撑其后方土体，从而使土体保持稳定。胡敏云通过假定圆弧曲线为拱轴线，以大小主应力理论建立了桩间净距的计算公式[12]：

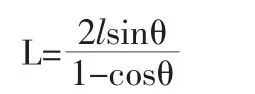
式中，l为拱高（m）；θ为大主应力拱切线方向与水平线的夹角（°）。

上述公式形式简单，并且可通过l值考虑桩间土剥落区域的合理范围，但把桩间土拱假定成圆弧曲线显得不太合理。李邵军通过有限元分析得到桩后存在四种土拱形态[13]，所以只通过大主应力拱一种形式进行分析并不太合理。贾海莉认为土拱效应中存在着大主应力拱和小主应力拱的共同作用，而抗滑桩作用的土体平面应分为稳定区、土拱区和自由区[14]。稳定区和土拱区的土体下滑力由大主应力拱承担，自由区土体下滑力主要由小主应力拱承担。考虑到稳定区和自由区土体稳定的重要性，通过大主应力拱的作用建立了桩间净距的计算式：

式中，p为土拱后作用的均布水平荷载（kN/m）；C为土体的粘聚力（kPa）；φ为土体的内摩擦角（°）；A=π/4+φ/2 ；d为土拱宽度（m）。

贾海莉法将桩作用土体平面分区，分清了阻滑主次，在桩间距的计算中突出了重点。但是在计算中忽略了小主应力拱的作用，结果往往偏大，如果运用上述公式布置桩位，难以保证自由区土体的稳定性，所以在必要时应同时考虑大小主应力拱的作用。

1.3 强度条件法

以土拱强度条件为基础确定桩间距的方法，统称为强度条件法。仅通过强度条件难以得到可靠桩间距，例如常保平法[15]计算结果存在一定的偏差。因此强度条件必须和静力平衡条件同时考虑，才能较为准确的计算合理桩间距的大小。

1.3.1 根据桩间水平土拱强度条件建立的桩间距计算方法周德培认为桩间土拱的形式为二脚拱，提出矩形截面桩间土拱应满足三个强度条件：（1）桩侧摩阻力之和不小于桩间作用于土拱上的压力；（2）跨中截面处前缘点应该满足莫尔-库仑强度准则；（3）桩体后侧的三角形受压区应能满足强度条件[16]。综合上述条件建立最大桩间净距的计算公式：

式中，q为作用于单位高度土拱上的桩后坡体线分布压力（kN/m）；c为桩间后侧土体的粘聚力（kPa）； φ为桩间后侧土体的内摩擦角（°）；α为三角形受压区斜边与水平方向的夹角（°）；b为桩径（m）。

周培德法确定的桩间距满足了土拱的强度条件，但却假定了土拱沿桩长均匀分布，而在实践中土拱是由桩顶向下逐渐减小的，这无疑夸大了土拱效应，使得桩间距计算结果偏大，所以必须除以适当的安全系数[17]来作为实际桩间距。赵明华将合理拱轴线作为土拱轴线，因为抗滑桩在阻滑过程中是被动受力的，所以假定拱轴线起点切向角β=π/4+φ/2，结合桩侧摩阻力之和应大于土拱所受压力与跨中截面处土体应满足的强度条件，得到计算公式[18]：

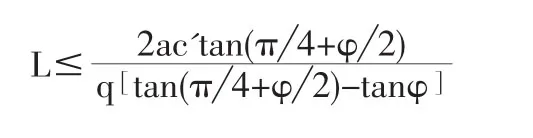
式中，L为桩间净距（m）；q为土拱后作用的均布水平荷载（kN/m）；a为抗滑桩侧面宽度（m）；φ'、c'分别为滑坡体与桩体间的内摩擦角（°）和粘聚力（kPa）；φ为室内试验给出的接触面上的内摩擦角（°）。

由于土体参数具有变异性，且对模型本身进行了简化假定，桩距计算必须根据工程实际进行综合考虑。而在拱角问题的处理上，目前意见仍不统一，需要今后深入研究。刘静认为土拱存在三种破坏形式：（1）土拱水平方向的平衡失效；（2）土拱竖直方向的平衡失效；（3）土拱拱脚处材料的强度失效[19]。结合这三种破坏形式获得相应的平衡控制条件，得到以下公式：

合理桩间距为：

S=Lmax+b

式中，L1为保证拱脚最不利破坏面土体抗剪强度的合理桩间净距（m）；L2为保证土拱水平向和竖向平衡的合理桩间净距（m）；φ为土体的内摩擦角（°）；φ'为土体与桩体间的内摩擦角（°）； c'为土体与桩体间的粘聚力（kPa）；b为桩侧宽（m）；q为土拱后作用的均布水平荷载（kN/m）；c为土体的粘聚力（kPa）。

刘静法对土拱拱脚给予了较大的重视，分别从水平和竖直方向阐明了其对于土拱强度的重要性，但其虽然综合考虑了静力平衡和土拱强度条件，但没有考虑土拱顶部的强度条件，可能会使计算结果偏大。

1.3.2 根据斜拱效应建立的桩间距计算方法

大部分计算方法都将抗滑桩后的土体假定为水平，但实际上滑坡的坡面往往是倾斜的。赵明华考虑了边坡倾角对桩间距的影响，在假定土拱的轴线为抛物线的基础上，根据水平面、竖直面内的静力平衡条件和强度条件，分别推导出两个桩间净距的计算公式[20]：

水平方向：

竖直方向：

式中，q为作用于单位高度土拱上的桩后坡体线分布压力（kN/m）；α为坡面与水平面的夹角（°）；c为桩间后侧土体的黏聚力（kPa）；φ为桩间后侧土体的内摩擦角（°）；b为桩正面宽度（m）。

从两个桩间净距的计算公式可知，存在一个临界角度α0，当坡面角α>α0时，竖直面内的强度破坏为主要控制条件，这时取L2为抗滑桩的桩间净距；当α<α0时，水平面内土拱截面的强度破坏为主要控制条件，这时则取L1为抗滑桩的桩间净距[22]。在实际的抗滑桩间距设计中，应分别计算两个桩间距，取两者中较小者为合理桩间距。在滑坡治理中由于抗滑桩的截面较大而常常设置混凝土或钢筋混凝土护壁，护壁及护壁周围浆液渗透的一定范围得到改良或加固的土体—接触带，对滑坡均起提供抗力的作用[21]。而在土拱拱角的处理上，上述公式均没有考虑接触带的作用。

1.3.3 根据三维有限元模型建立的桩间距计算方法

大多数桩间距计算都将模型简化为平面模型，而桩间土拱效应的几何形态在竖向上是呈不规则分布的[13]，所以上述方法将土拱效应在竖向上作了近似处理。张永兴考虑了土体自重应力的影响，通过有限元法建立了三维计算模型，并推导出最大桩间净距计算公式[22]：

式中，δ为拱脚形状系数，δ=1/cosθ，θ为拱脚处拱轴线的切线与水平线夹角（°）；c为滑体的凝聚力（kPa）；t为拱脚厚度（m）；φ为内摩擦角（°）；σN为轴应力（kN）；q（z）为土拱上作用单位面积的土压力（kN/m2）；

通过有限元建立三维模型可以较为真实的模拟边坡环境，并且可以考虑到土体自重应力对土拱的影响。但是利用有限元进行模拟的技术现在仍然不够成熟，需要今后继续完善。

2 几种计算方法的比较

采用同样的工程实例分别用上述计算方法计算，结果见表1。从表中可以看出，不同计算方法得到的桩间距差别很大。对于截面为2.0m×3.0m的抗滑桩，在同一滑坡推力的作用下方法2、4计算结果偏大，方法3、5计算结果偏小，其他方法计算的桩间净距介于5～8m之间。

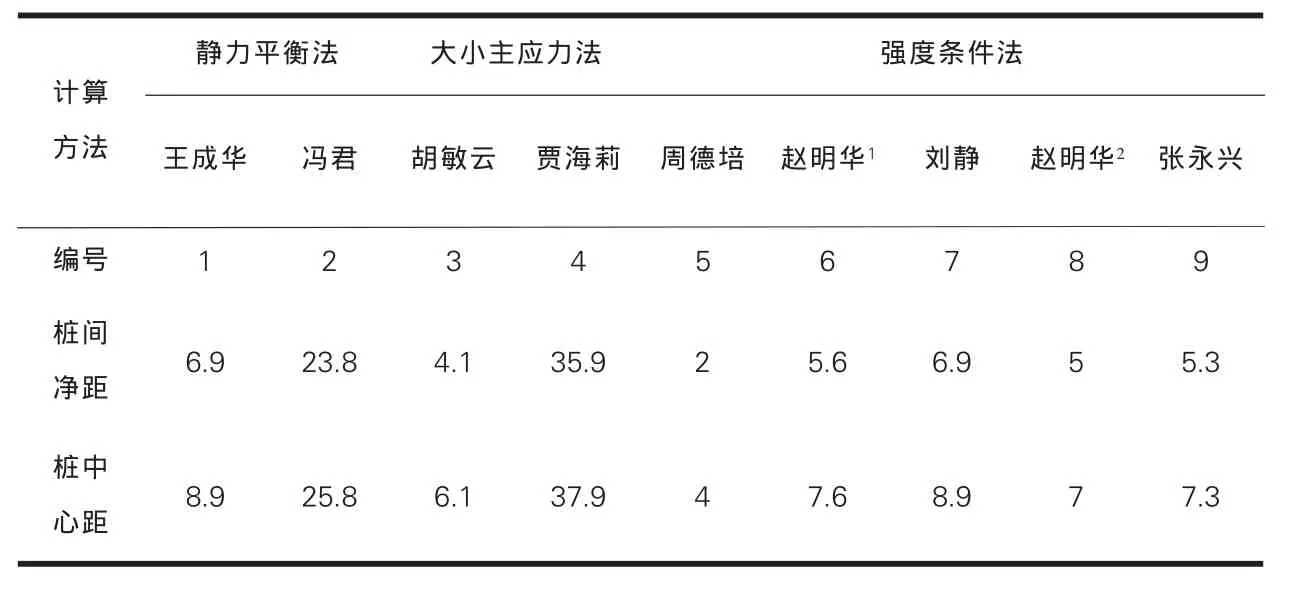
表1 各种算法计算结果对照表（单位：m）

3 存在的问题及建议

抗滑桩合理桩间距分析是一个受多种因素影响的问题，而桩间距的确定对抗滑桩阻滑性能的发挥、成本的控制起着重要作用，虽然已经有很多通过土拱效应计算桩间距的方法，但其中仍然存在一些问题需要进一步探讨：

（1）土拱的静力平衡条件对桩间距的影响较大，但很多方法在滑坡推力的承担问题上相异。若单一以桩侧摩阻力承担滑坡推力会使计算偏于保守，而桩前土体的阻滑作用并不明显，提供抗滑力显然不太合理，并且土拱自身的剩余抗滑力受土体参数的影响较大，所以明确阻滑条件是今后研究值得注意的问题。

（2）桩间土拱边界是一个模糊的范围。由于土拱的组成物和结构与前后土体完全相同，所以桩间土拱与前后土体没有明显的界限，土拱沿滑动方向的厚度也不清楚。因此将桩间土体的支撑作用适当分类，找出主要受力部分，从而得到桩间距的主要控制项是今后研究的重点。

（3）在桩间距的计算中，不同的土拱形式假定会对土拱受力情况产生影响，从而产生不同的计算结果，所以如何对土拱形式进行准确的描述有待今后继续研究。

（4）土拱效应具有时空特性，而大部分计算模型都将其简化为平面问题，并忽略了地震、渗透等作用的影响，这很容易造成计算的失真，从而影响桩间距的确定，因此应结合土拱效应的时空特性来确定合理桩间距。

（5）在计算桩间距时，没有考虑抗滑桩本身的力学性质、截面形状及其锚固深度等对土拱效应的影响，会使计算失真，所以这一问题有待进一步研究。

（6）如今大部分计算都集中在单排桩桩间距的确定上，但随着抗滑桩的不断发展，多排桩的大量运用是一个不可避免的趋势，因此有必要结合土拱效应的作用对多排桩的桩间距问题进行探讨。

（7）利用数值模拟的方法可以从不同角度观察土拱效应对于桩间距的影响，并可以在成本较低的情况下，相对容易的获取土拱各个性状的参数。所以数值模拟法是今后土拱效应研究发展的趋势。

[1]殷跃平，康宏达，陈波.三峡工程移民迁建区灾害地质体改造与利用研究[J].工程地质学报，2000，8（1）:73-80.

[2]王成华，陈永波.世寿街滑坡发生机理与防治对策[J].工程地质学报，2000，8（3）:277-280.

[3]郑颖人，陈祖煜，王贡先，等.边坡与滑坡工程治理[M].北京：人民交通出版社，2007:394-395.

[4]吴子树，张利民，胡定.土拱的形成机制及存在条件的探讨[J].成都科技大学学报，1995（2）:15-19.

[5]张建华，谢强，张照秀.抗滑桩结构的土拱效应及其数值模拟[J].岩石力学与工程学报，2004，23（4）:669-703.

[6]王士川，陈立新.抗滑桩间距的下限解[J].工业建筑，1997，27（10）:32-36.

[7]王成华，陈永波.抗滑桩间土拱力学特性与最大桩间距分析[J].山地学报，2001（6）：556-559.

[8]冯君，吕和林，土成华.普氏理论在确定抗滑桩间距中的应用[J].中国铁道科学，2003，24（6）:79-81.

[9]厚美瑛，陆坤权.奇异的颗粒物质 [J].新材料产业，2001，（2）:26-28.

[10]胡敏云，夏永承，高渠清.无锚撑桩排式支护护壁桩侧土压力计算方法[J].岩石力学与工程学报，2000，19（4）:517-521.

[11]WILLIAMS K H.Arch in soil arching [J].Journal of Geotechnical Engineering，1989，115（3）:415-419.

[12]胡敏云.深基坑护壁桩间距确定方法探讨[J].中国公路学报，2001，14（2）：27—29.

[13]李邵军，陈静，练操.边坡桩-土相互作用的土拱力学模型与桩间距问题[J].岩土力学2010，31（5）:1352-1357.

[14]贾海莉，王成华.基于土拱效应的抗滑桩与护壁桩的桩间距分析[J].工程地质学报，2004，12（1）:98-103.

[15]常保平.抗滑桩的桩间土拱和临界间距问题探讨:滑坡文集（第十三集）[M].北京:中国铁道出版社，1998.73-78.

[16]周德培，肖世国.边坡工程中抗滑桩合理桩间距的探讨[J].岩土工程学报，2004，26（1）:132-135.

[17]铁道部第一勘测设计院.铁路工程设计技术手册:路基[M].北京:中国铁道出版社，1995.

[18]赵明华，陈炳初，刘建华.考虑土拱效应的抗滑桩合理桩间距分析[J].中南公路工程，2006，31（2）:1-4.

[19]刘静，吴海涛，胡焕校.由桩后土拱形成的条件对抗滑桩间距的计算[J].山西建筑，2009，35（36）:1-2.

[20]赵明华，廖彬彬，刘思思.基于拱效应的边坡抗滑桩桩间距计算[J].岩土力学，2010，31（4）:1211-1216.

[21]雷用，赵尚毅，郝江南，等.支挡结构设计与施工[M].北京:中国建筑工业出版社，2010:22-23.

[22]张永兴.考虑自重应力的悬臂式抗滑桩三维土拱效应及合理间距研究[J].中国公路学报2009，（2）：18-25.