公路粉细砂地基稳定性分析与评价

杨 戈，谭 鹏，王 朋

（同济大学，上海市 200092）

0 引言

滨海地区的公路多建于粉细砂地基之上。粉细砂地基承载力较低，表层粉细砂松散。公路建成之后，公路粉细砂地基中的应力包括两个部分，即由土中上覆地基、路基和路面结构自身重量而产生的自重应力和车辆荷载作用下产生的荷载应力。自重应力随着上覆结构厚度的增加线性增长，而由车辆荷载引起的荷载应力则随下部结构深度的增加逐渐减小，当深度达到一定值后，由车载引起的附加应力σZ与路基自重应力σc的比值很小（0.1～0.2），此时可忽略车辆荷载的影响，这一深度即为由车辆荷载引起的路基附加应力分布范围，称为路基工作区深度。粉细砂地基的稳定性对于保证上部路基路面结构的强度和稳定性要求极为重要。粉细砂地基中的附加应力主要由路基高度和车辆轴载决定。当路基高度达到一定值后，由车载引起的附加应力可以在路基内充分扩散，此时对粉细砂地基稳定产生影响的主要是工程荷载产生的静应力；当路基高度较低时，由车载引起的附加应力会作用到粉细砂地基中，交通动载有可能造成粉细砂地基振动液化。

本文拟从以下3个方面对公路粉细砂地基的稳定性进行分析与评价。第一方面内容是指粉细砂地基的承载力不足以承受上部荷重而导致的粉细砂地基的强度和稳定性问题；第二方面内容是指粉细砂地基的振动液化问题；第三方面内容是指粉细砂地基发生沿深层滑裂面滑动的稳定性问题。

1 粉细砂地基承载力分析

在进行粉细砂地基承载力分析前，首先应计算分析不同路基高度下粉细砂地基中的应力水平，从而与粉细砂地基的承载力进行比较。

在《公路设计手册－路基》[1]中，车载在路基土中引起的荷载应力采用基于弹性半空间体理论的布氏课题公式进行计算，路面各个结构层按一定准则换算为当量路基土层厚度，如式（1）所示：

式（1）中：he为路面结构层换算为路基土层的当量厚度；h1为路面结构层厚度；E1为路面结构层模量；E0为路基模量；m为指数，多层柔性路面为2.5。

这种换算方法存在几个问题。

（1）由于车辆荷载直接作用于路面表面，因此，即使对路面结构做了模量等效换算，弹性半空间体理论依然无法模拟路面各结构层与路基材料特性的差异，以及由此造成的应力扩散效应的差异。

（2）未考虑不同轴型的荷载叠加效应，当车辆为双轴或三轴及其以上时，经理论分析和现场实测表明，路基中最大荷载应力并不在通常认为的（单轴）轮隙中心处正下方，这正是由于多轴荷载叠加所造成的。

基于此，计算中采用弹性层状体系理论计算不同路面结构、轴型（考虑荷载叠加效应）、轴重（考虑超限）情况下路基沿深度方向的竖向附加应力分布情况，使用不同的判断标准求取路基工作区深度范围，并对不同工况条件下的路基工作区深度做统计分析。

利用SHELL公司的BISAR3.0程序计算各种轴型在各级轴载作用下路基深度方向的附加应力。图1所示为轮载的平面分布图，其中，x为车轴方向，y为行车方向。参照规范要求，轮载采用圆形均布荷载，单轮传压面当量圆半径按式（2）计算。

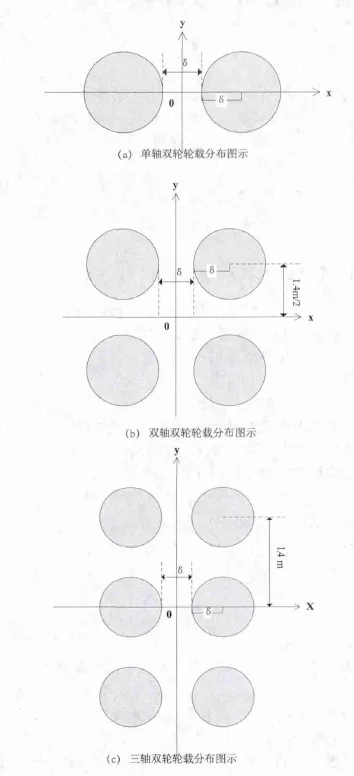
图1 轮载的平面分布图

为简化计算，不考虑相同车道上轮载的叠加效应，由于相邻车道的车辆在同一横断面出现的概率很小，相邻车道上轮载的叠加效应也不予考虑。通过试算，同一深度处路基应力最大的位置在原点处（见图1），因此，计算点的平面坐标均为（0，0）。图2所示为路基（荷载）应力计算模型，z为路基深度方向。

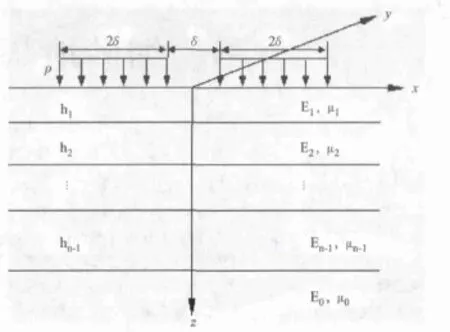
图2 路基应力计算模型

计算点位从路基顶面开始，一直到路基顶面以下3.7 m处结束（除前三个点分别为路基顶面以下0 m、0.8 m、1 m以外，其余各点均是在前一点基础上增加0.1 m），共计29个点。

式（2）中：δ为单轮传压面当量圆半径；P为单轮轮重；p为轮胎接地压力。

路基应力计算采用的轴型有单轴（双轮）、双轴（双轮）、三轴（双轮）三种型式。《公路沥青路面设计规范》（JTG D50—2006）[2]3.1.2中轴载换算公式的上限（单轴）轴载为130 kN。根据相关文献[3-4]，公路上实际行驶的车辆，其极限（单轴）轴载可达240 kN。东郊至龙楼公路设计文件表明：该公路属于双向4车道1级公路，同时也是文昌航天发射场的配套道路，将承载5 M火箭公路运输车荷载，火箭运输车最大轴载可达260 kN，具体尺寸如图3所示。

图3 5 M火箭公路运输车车型图(单位：cm)

计算中（单根）轴重取100 kN（标准轴载）、130kN、160 kN、240 kN、260 kN 5种级位。查阅相关文献，重载车辆的轮胎内压上限多在1.0 MPa左右，据此，计算中轮胎接地压力按轴重大小取0.7～1.0 MPa。

此外，设计文件表明，东郊至龙楼公路路面结构及相关参数如表1所示，路基应力计算工况如表2所示。

各工况路基应力计算结果如表3所示。

通过对粉细砂公路的应力水平分析可知，即使是5 M火箭运输车在路床低引起的附加应力也不过21.07 kPa，而3 m高的路基在上部路基路面结构的自重作用下，其基底自重应力达到了73.86 kPa。

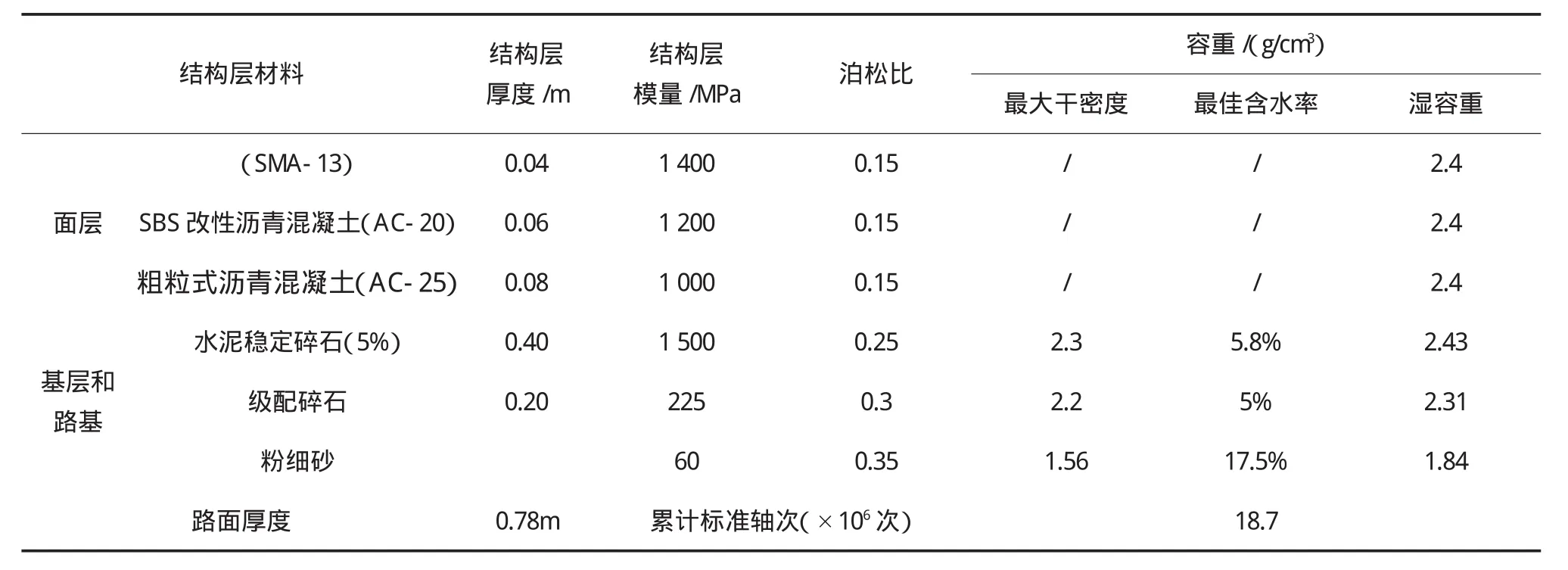
表1 东郊至龙楼公路路面结构（路基应力计算所选路面结构）

表2 路基应力计算工况

根据依托工程勘察报告可知，滨海粉细砂地基的承载力基本容许值大多在70～130 kPa之间。这意味着对于3 m以下的中低粉细砂路堤段，粉细砂地基不会发生因承载力不足而导致的强度和稳定问题；对于3 m以上的高路堤，若其下的粉细砂地基承载力较低，就有可能因地基承载力不足而导致粉细砂地基失稳。因此，对于承载力较低的粉细砂地基，应采用相应方式进行处理，以提高粉细砂地基的承载力。

2 粉细砂地基振动液化分析

砂发生液化需要具备一定的条件，可将液化发生的条件分为内部条件与外部条件:内部条件主要指砂的颗粒特性、密实状态；外部条件主要指砂的饱和状态、排水条件、荷载条件。

2.1 液化内部条件分析

2.1.1 颗粒特性

填料的粒径与级配特性对填料的液化性质影响很大，D50在0.05～0.09 mm之间最容易液化，D50越大，抗液化强度就越大，同时，级配均匀的填料比级配不均匀的更容易液化[5]。通过筛分试验得到滨海细砂D50，如表4。由表4可知，滨海细砂D50远远大于0.05～0.09 mm的液化危险范围，颗粒级配不良，可以认为具有较强的抗液化的能力。

表3 应力计算结果

表4 滨海细砂D50

2.1.2 密实状态

浅层的粉细砂多处于松散状态，因此，从预防振动液化的角度而言，粉细砂地基应采用相关措施增加浅层地基的密实度，增强粉细砂地基抗液化能力。

2.2 液化外部条件分析

2.2.1 饱和状态

砂土液化只有在饱和状态下才可能发生。滨海地区地下水水位埋深大多在0.65～1.0 m范围，地下水位以下的饱和粉细砂较为松散，这些因素有可能促使振动液化产生，因此，应采用相应措施降低地下水位高度，同时提高浅层粉细砂的密实度，做到从根本上防止粉细砂地基振动液化现象的产生。

2.2.2 排水条件

粉细砂渗透系数大，在边界排水条件好的情况下因振动产生的超孔隙水压力会迅速消散，因此，良好的排水设施有助于防止粉细砂地基的振动液化产生。

2.2.3 荷载条件

粉细砂渗透系数大，在设置了良好边界排水的前提下，重复作用的外荷载必须达到相当高的强度和频率，并且作用较长时间，才可能使砂体内部的超孔隙水压力发生累积。交通荷载在强度、频率、作用时间上都达不到产生液化的要求。

综上所述，虽然粉细砂自身具有较强的抗液化能力，但浅层粉细砂地基存在松散、饱和的现象，有可能出现粉细砂地基振动液化现象，因此，对粉细砂地基应进行处理，以达到提高粉细砂地基密实度，同时防止浅层粉细砂处于饱和状态的目的。

3 粉细砂地基深层失稳分析

《建筑地基基础设计规范》（GB 50007—2011）[6]规定：一般建筑物在满足地基承载力的条件下，不需要进行地基稳定性计算，但若遇到下列情况，则应进行地基稳定性验算：其一，经常受水平荷载作用的高层建筑和高耸结构物；其二，建造在斜坡或坡顶上的建筑物。对公路粉细砂地基稳定性的验算可采用圆弧滑动面法。圆弧滑动面法就是将地基滑裂面简化为圆弧面，验算地基土体沿深层滑裂面滑动的稳定性，地基的圆弧滑动法与边坡圆弧滑动法相似，一般采用条分法。

条分法分析稳定性问题有以下几个步骤：（1）按比例绘出地基滑裂面剖面；（2）任选一圆心，确定滑裂面，将滑裂面以上土体分成几个等宽或不等宽土条；（3）每个土条的受力分析，根据平衡条件建立方程（假设土条两侧的作用力相互抵消）；（4）计算滑裂面上的总滑动力矩和总抗滑力矩；（5）通过总滑动力矩和抗滑力矩，确定安全系数，如下式：

对于公路粉细砂地基的稳定评价，需比较地基中的应力水平和粉细砂地基承载力的大小，并通过条分法试算出安全系数，以达到稳定性评价的目的。条分法是一种试算法，人工计算工作量繁琐且效率低下，实际应用可采用岩土理正软件中的瑞典条分法对粉细砂地基进行稳定性验算与评价。

3.1 稳定验算算例

算例中，路堤高度为3 m，路堤顶宽为24.5 m，边坡坡度为1∶1.5。计算过程中分两级施加路基填土荷载，工后沉降基准期结束时间为6个月。计算图示及相关参数如图4，表5，表6。

图4 结构图示（单位：m）

表5 相关参数

表6 加载时间及高度

3.2 固结度计算参数

地基土层底面不设排水层，固结度计算方法采用微分方程数值解法，多级加荷固结度修正时的荷载增量定义为“填土高*容重”，填土-时间-固结度输出位置距中线距离为 0.000(m)，填土-时间-固结度输出位置深度为0.000(m)。

3.3 稳定计算参数

稳定计算方法采用总应力法(瑞典条分法)，稳定计算不考虑超载，稳定计算不考虑地震力，稳定计算目标为给定圆心、半径计算安全系数，圆心X坐标为 -2.000 m，圆心Y坐标为 20.000 m，半径为35.000 m，条分法的土条宽度为1.000 m。

3.4 稳定计算结果

（1）第1级加荷,从0.0～3.0月,路基设计高度1.500 m,路基计算高度(考虑沉降影响)1.526 m，加载结束时稳定结果。滑动圆心=(-2.000,20.000)m，滑动半径=35.000 m，总的下滑力=332.745 kN，总的抗滑力=4 786.110 kN，土体部分下滑力=332.745 kN，土体部分抗滑力=4 786.110 kN，滑动安全系数=14.384。

（2）第2级加荷,从4.0～6.0月,路基设计高度3.000 m,路基计算高度(考虑沉降影响)3.066 m，加载结束时稳定结果。滑动圆心=(-2.000,20.000)m，滑动半径=35.000 m，总的下滑力=643.091 kN，总的抗滑力=5 110.200 kN，土体部分下滑力=643.091 kN，土体部分抗滑力=5 110.200 kN，滑动安全系数=7.946。

由上述各级加载结束后的地基稳定计算结果可知，施工期间以及竣工后，粉细砂地基的滑动安全系数均远大于1.2，故粉细砂地基处于稳定状态。鉴于计算工况的保守性，粉细砂地基在施工过程中的滑动安全系数远远大于规范规定的容许值，因此，粉细砂地基不会出现沿地基深层滑裂面滑动失稳的现象。

4 结论

对于公路粉细砂地基稳定的评价主要通过粉细砂地基的承载力大小、粉细砂颗粒D50的大小以及粉细砂沿深层滑裂面滑动的稳定安全系数来实现。对于公路粉细砂地基稳定验算主要通过圆弧滑动面法（条分法）来实现的。

公路粉细砂地基的稳定验算与评价方法的研究结果表明，对于承载力较低并且承受3 m以上高路堤的粉细砂地基，可能存在粉细砂地基承载力不足以承受上部荷载而导致的强度和稳定性问题；对于承载力较低并且承受3 m以下中低路堤的粉细砂地基，不存在承载力不足的问题。天然的粉细砂地基有可能出现振动液化的现象，粉细砂地基不会发生沿地基深层滑裂面滑动失稳的问题，因此，天然的粉细砂地基应采取措施予以处理，以达到提高天然粉细砂地基承载力和密实度，降低地下水位高度，防止浅层地基处于饱和状态的目的。

[1]交通部第二公路勘察设计院.公路设计手册——路基［M］.北京：人民交通出版社，1996.

[2]JTG D50—2006，公路沥青路面设计规范［S］.

[3]胡小弟.轮胎接地压力分布实测及沥青路面力学响应分析［D］.上海：同济大学，2003.

[4]钱国平.重载条件下沥青路面结构复杂受力特征及力学响应研究［D］.上海：同济大学，2004.

[5]高大钊.土质学与土力学[M].北京：人民交通出版社，2000.

[6]GB 50007—2011，建筑地基基础设计规范［S］.