城市居民步行出行距离分布规律研究
2014-01-08程灿,王珏
程 灿,王 珏
(无锡市政设计研究院有限公司,江苏无锡 214072)
0 引言
随着我国城市规模的不断扩大,人口数量的增加,城市居民的出行越来越频繁,日益严重的交通问题极大影响了城市的发展进程,迫切需要我们找到解决交通问题特别是客运交通问题的方法,而对城市居民出行特征的研究是其中不可缺少的工作[1]。城市居民的出行具有时间和空间的分布,不同的出行目的和不同交通方式的出行距离不同。出行距离是一次出行从起点到目的地之间的距离。交通规划者们最关心的就是个体交通在空间上积聚所带来的问题。由于各种交通方式所适宜的出行距离不同,因此,出行者在空间积聚的过程必然促使不同的交通方式在空间上呈现出不同的出行距离范围。另外,研究居民各种交通方式的出行距离也可以为城市构成要素的合理布局、城市客运交通方式结构的合理配套提供依据。
现有关于每种交通方式出行距离的分析,有一些简单的总结性结论[2-3]。关于出行距离分布特征的研究,国内学者最早的研究来自吉林大学的刘伟平提出的负指数分布,他把出行距离作为随机变量,证明了此随机变量服从负指数分布[4]。另一项研究成果是西南交通大学的陈尚云等提出的二阶爱尔兰分布模型,研究者在分析城市土地利用形态的基础上,建立了数学模型,模拟城市土地利用形态的不同种类,计算城市出行总量的距离分布和空间分布,总结出反映城市出行总量距离分布的二阶爱尔兰分布模型[5-6]。文献[7]对机动车出行距离的量化分析有分布函数的拟合等,但对其它交通方式定量分析较少。
本文拟从各城市的调查数据的分析出发,建立各交通方式的出行距离分布函数。为了体现分布函数在各城市的区别,先根据数据建立模型,再用一些与出行距离分布有关的因素来拟合模型中的参数。
1 研究方法
在统计分析数据时,如果不能马上根据专业知识或者观测量数据本身的特点确定一种最佳模型,可以利用曲线估计在每种不同的曲线回归模型中选择建立一个简单而又比较合适的模型。
曲线估计的数据要求是:自变量与因变量应该是数值型变量;模型的残差应该是任意并且呈现正态分布。
大多数情况下,对变量之间关系的认识往往不是很清楚,需要先绘制散点图,根据数据分布特点,确定应采用的模型。可以多制定几个模型进行拟合,根据输出的统计量,结合图形综合考虑,确定最佳模型。
在曲线估计的基础上,建立回归建模(regression analysis)。典型的回归模型有3种[8]。
(1)一般多元线性回归模型:Y=β0+β1X1+β2X2+β3X3+…e,它是所有回归模型中最为简单的一种,常用最小二乘法处理。
(2)一元非线性回归分析模型:在一元非线性回归分析时,曲线模型的种类很多,最常见的模型有逆线性模型(其数学公式为Y=a+b/X)、指数模型Y=a×ebx+k等。
(3)多元多项式回归模型:二元及二元以上的回归模型都可以称为多元回归模型,其中二元回归模型一般形式为 Y=β0+β1X1+β11X12+β2X2+β22X22+β23X2X3+…+e。多元多项式回归模型一般形式与二元回归模型类似,但形式更加繁琐。
2 步行出行距离结构特征
各城市步行方式的出行距离分布统计数据如图1所示。
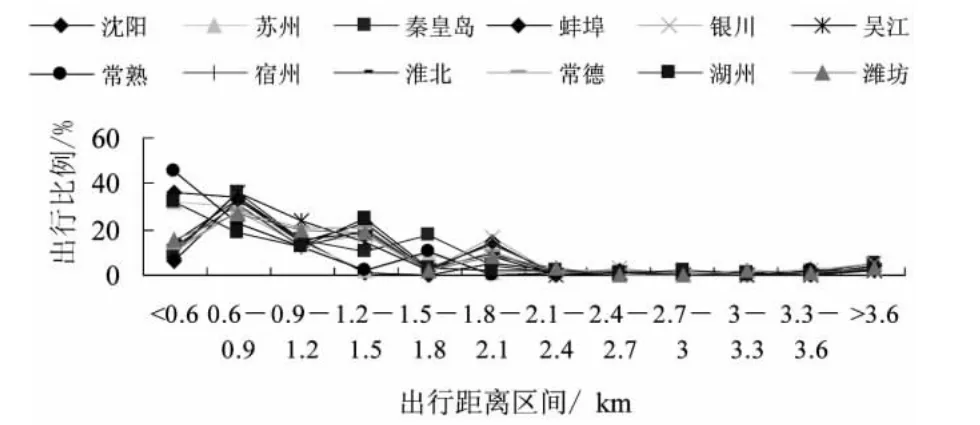
图1 步行的出行距离结构分析
从图1中可以清楚判断,虽然城市之间存在差别,但明显的是步行主要集中在0.6~0.9 km区间,其余区间并不突出。出行距离结构组成特性突出,是步行交通方式的适应性决定的,因为步行方式属于短距离出行方式,在极短距离出行时有不可替代的绝对优势。根据调查数据可以计算累计分布概率,画出累计分布趋势,如图2所示。
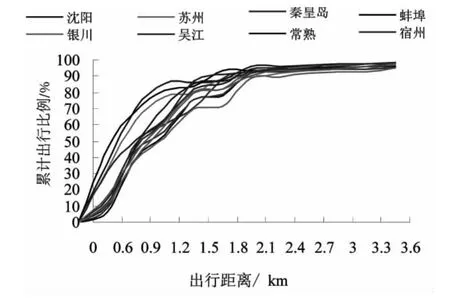
图2 步行出行距离的累计分布趋势曲线
3 数据拟合
在数据拟合过程中,原始数据的出行距离s的范围是0≤s≤3.6(km)。为了提高精确度,步行的分布函数F1(s)的单位为%,即0≤F1(s)≤100。为了更好地确定数据模型,运用SPSS软件对各个城市数据进行了多种模型拟合(包括Linear:Y=b0+b1X;Quadratic:Y=b0+b1X+b2X2;Power:Y=b0Xb1;Cubic:Y=b0+b1X+b2X2+b3X3;Growth:Y=e(b0+b1x);Exponential:Y=b0+eb1x),另外也试验了适合机动车出行距离分布的二阶Weibull分布函数:Y=1-eb*X。发现精确度最高的是Cubic模型,因为当距离为0时分布概率也为0,所以在模型参数设定时要设定一次项的系数为0,即模型形式为:Fa(s)=b3s3+b2s2+b1s。各城市的拟合情况见表1。
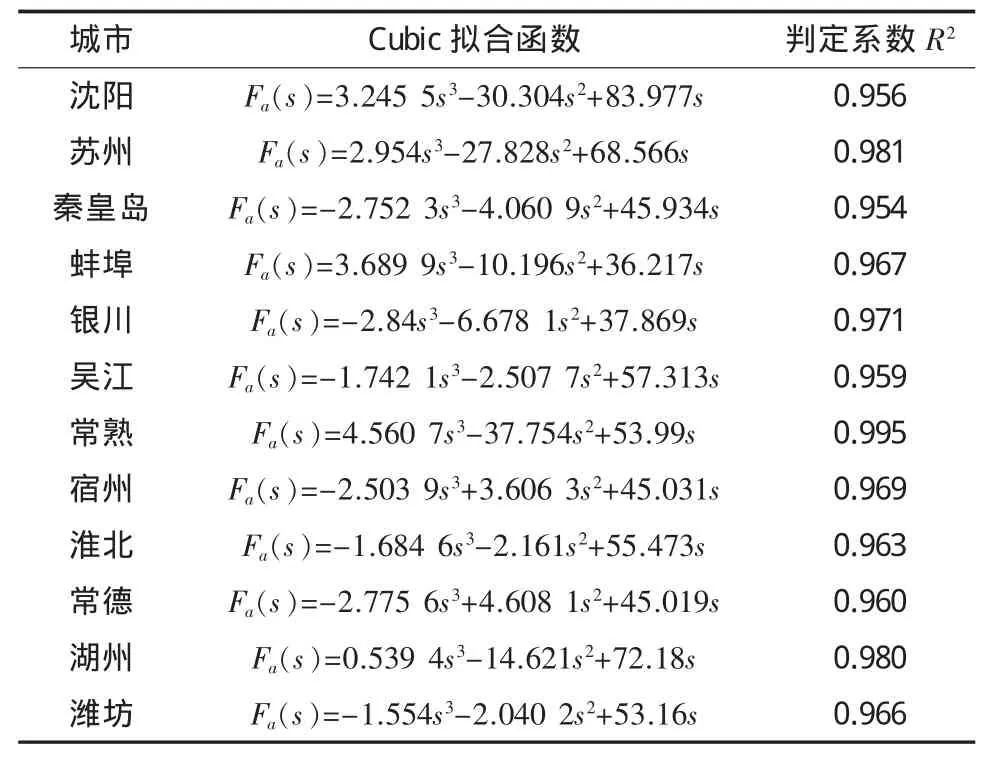
表1 各城市步行距离累计分布函数的拟合
4 参数确定
所有城市特性数据为交通规划居民出行调查当年数据,所以只与该城市的出行距离有关,不存在横向对比性。
影响出行距离分布的因素有许多,城市的用地规模是直接的因素,经济水平等也决定着各方式的出行距离。在城市特性统计中,统计了城市规模(用地规模(建成区面积)、人口规模(市区总人口))和经济水平(总GDP和人均GDP),见表2。发现模型三次项系数的变化趋势与人均GDP(g)的变化趋势大致相同,两者相关性较高。因此通过人均GDP这个变量来拟合,即:


表2 城市特性数据和方式分担情况(按人均GDP从高到低排列)
拟合过程中发现直接拟合精确度判定系数为0.91,但剔除一个误差数据后重新拟合,得到了0.96的精确度,因此用后者的模型来拟合三次项系数 b3,见式(2):

式(2)中,G的单位是万元。
二次项系数b2与三次项系数b3之间的线性拟合精确度为0.998,因此用三次项系数来表示二次项系数:

统计数据中一次项系数的变化范围,当b3>0,54<b1<84;b3<0,36<b1<57,故也用三次项系数b3来拟合 b1:

通过以上的拟合可以得出模型各项的系数值,可以进行出行距离分析。
5 结论
本文在文献综述的基础上,以已知的城市居民出行数据为拟合资料,建立了步行的出行距离分布的统计模型,通过探讨分布函数参数的相关影响因素,得到能够反映某一城市的出行分布特征的一般模型,为城市规划和城市交通规划提供了重要的决策依据。
另外,出行距离分布特征研究还具备以下的应用和研究前景。
(1)可作为交通需求预测中交通分布预测重力模型的阻抗函数,改良了传统的幂函数和指数函数,且不存在区内出行量过大的问题,为新阻抗函数的应用提供了理论基础。
(2)若知道各出行方式的距离曲线,配以出行距离分布函数,则可以得到不同距离的某种出行方式的出行量,进一步得到城市总体交通结构[5]。
(3)若已知各小区的发生吸引量,配以出行分布函数,则可以很方便地通过迭代计算得到出行的OD分布。
[1]颜敏.城市居民出行距离影响因素研究[D].成都:西南交通大学,2008.
[2]毛海虓.中国城市居民出行特征研究[D].北京:北京工业大学,2005.
[3]陈尚云.我国特大城市客运交通系统结构和发展战略研究[D].成都:西南交通大学,2004.
[4]刘伟平.交通 OD表的实用计算模型 [J].中国公路学报,1995,8(3):18-24.
[5]陈尚云,杜文,高世廉.我国特大城市出行分布模型及其参数的研究[J].系统工程,2002,20(4):63-66.
[6]陈尚云,杜文.我国大城市用地形态与交通发展模式的研究[J].系统工程,2003,21(3):53-57.
[7]石飞.城市道路等级级配及布局方法研究[D].成都:东南大学,2006.
[8]王黎明,陈颖,杨楠.应用回归分析 [M].上海:复旦大学出版社,2008.
